Аннотация. Статья посвящена полуправильным многогранникам и их классификации.
Ключевые слова: архимедовы тела, каталановы тела, полуправильные многогранники
Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности - от маленького ребенка, играющего с кубиками, до взрослого человека.
Иоганн Кеплер называл куб "родителем" всех правильных многогранников. На основе куба он смог построить все другие виды правильных многогранников.
Правильные многогранники окружают нас везде, кажется что любая вещь состоит из правильных многогранников. А что же такое полуправильные многогранники и почему они так редко используются в окружающем мире?
Архимедовы тела
Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Архимедовы тела частично получаются из Платоновых тел в результате их усечения. Усеченное тело есть не что иное, как тело с отрезанной верхушкой. Так могут быть получены первые пять архимедовых тел: усеченный тетраэдр (рис.1), усеченный октаэдр (рис.2), усеченный икосаэдр (рис.3), усеченный куб (рис.4), усеченный додекаэдр (рис.5). Вторая группа архимедовых тел представлена двумя многогранниками, являющимися результатом пересечения двух Платоновых тел подходящих размеров и расположенных так, что их центры совпадают. Это кубооктаэдр (рис.6) - результат пересечения куба и октаэдра и икос, икосододекаэдр (рис.7) - результат пересечения икосаэдра и додекаэдра. В результате усечения кубооктаэдра и икосододекаэдра получены следующие два многогранника – ромбокубооктаэдр (рис.8) и ромбоикосододекаэдр (рис.9). Дальнейшее видоизменения могут превратить их в два других многогранника - усеченный кубооктаэдр (рис.10) и усеченный икосододекаэдр (рис.11). Последние два архимедовых тел - «курносый» куб (рис.12) и «курносый» додекаэдр (рис.13). Термин курносый означает, что каждую грань многогранника окружили треугольники, что каждое ребро заменили парой треугольников, а в каждой вершине добавили еще один многоугольник.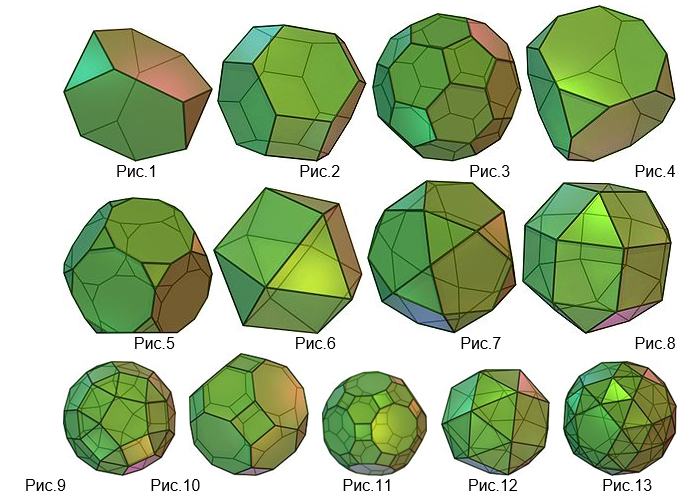
Прародителем каждого из 13-ти полуправильных многогранников является один из пяти Платоновых многогранников(рис.14) путем отсечения вершин. При дальнейшем усечении полученных тел мы получаем правильные многогранники, поэтому тел Архимеда только 13.
Каталановы тела
Двойственные архимедовым телам, так называемые каталановы тела, имеют конгруэнтные грани, равные двугранные углы и правильные многогранные углы. Каталановы тела тоже называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а Каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
То есть, полуправильными в этом случае называются тела, у которых отсутствует только одно из первых двух из следующих свойств правильных тел:
- Все грани являются правильными многоугольниками;
- Все грани одинаковы;
- Тело относится к одному из трёх существующих типов пространственной симметрии.
Архимедовы — тела, у которых отсутствует второе свойство, у каталановых отсутствует первое, третье свойство сохраняется для обоих видов тел.
Существует 13 архимедовых тел, два из которых (курносый куб и курносый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы. Соответственно, существует 13 каталановых тел.
Систематизация названий
1. Усеченный октаэдр:
Многие названия созданы на основе греческих приставок, означающих количество граней и корня -едр, означающего грань.
(-hedron- буквально значит место).
Октаэдр (от греч. οκτώ, «восемь»)
2. Усеченный икосододекаэдр:
икосо- (ikosi-) значит 20
додека- значит 2+10
-едр, означает грань
усечение (truncate) отсечение угла многогранника вокруг его вершины
3. Усеченный куб:
усечение (truncate) отсечение угла многогранника вокруг его вершины
4. Усеченный икосаэдр:
усечение (truncate) отсечение угла многогранника вокруг его вершины
икосо- (ikosi-) значит 20
-едр, означает грань
5. Усеченный додекаэдр:
Додека - значит 2+10 и используется для описания двенадцатигранника.
-едр, означает грань
усечение (truncate) отсечение угла многогранника вокруг его вершины
6. Курносый додекаэдр:
Додека - значит 2+10 и используется для описания двенадцатигранника.
7. Усеченный тетраэдр:
тетра- (tetra) – четыре.
8. Икосододекаэдр:
Додека - значит 2+10 и используется для описания двенадцатигранника.
икосо- (ikosi-) значит 20
9. Курносый куб:
10. Кубооктаэдр:
Октаэдр (от греч. οκτώ, «восемь»)
11. Усеченный кубооктаэдр:
усечение (truncate) отсечение угла многогранника вокруг его вершины
Октаэдр (от греч. οκτώ, «восемь»)
12. Ромбокубооктаэдр:
Приставки могут описывать форму граней, чтобы устранять противоречия между двумя многогранниками с одинаковым количеством граней.
13. Ромбоикосододекаэдр:
икосо- (ikosi-) значит 20
Додека - значит 2+10 и используется для описания двенадцатигранника.
Полуправильные многогранники в архитектуре
Национальная библиотека Беларуси(рис.15). Форма книгохранилища — ромбокубооктаэдр.
Библиотека — самый крупный из архитектурных ромбокубооктаэдров, возведенных в мире в настоящее время. Его высота составляет 73,6 м (23 этажа), а вес — 115 000 тонн.
Повторить в архитектуре сложные многогранники (особенно, архимедовы тела — к которым, в том числе, относится и ромбокубооктаэдр) действительно нелегко. И если случается, то в меньшем масштабе, чем Нацбиблиотека, и усеченной форме.
Благодаря оригинальному архитектурному решению в новом здании НББ стало возможным гармонично совмещать искусственные и естественные материалы для отделки интерьеров, создать особый световой колорит во внутреннем пространстве библиотеки за счет сочетания естественного света с искусственным освещением и обеспечить психологический комфорт посетителей и сотрудников

Рис.16
Музей архитектуры Тойо Ито(рис.16) на острове Омишима (Япония) — в основе дизайна музея лежат геометрические фигуры: октаэдр, тетраэдр и кубооктаэдр.

Рис.17
Здание Международного экономического комитета в Киеве(рис.17), купол конференц-зала своими гранями образует икосододекаэдр.
Рис.18
Ботанический сад «Эдем»(рис.18) в Корнуолле (Великобритания) был построен в 2001 году на месте выработанного мелового карьера, а для конструкций сводов использовались формы шестигранных сот. А это еще один вид многогранников — усеченный икосаэдр. Состоит из 12-ти пятиугольников и 20-ти шестиугольников.
Рис.19
Усеченная пирамида пользуется популярностью у современных архитекторов. Например, в Индианополисе (США) в 1972 году закончили строительство офисного комплекса из трех зданий, который так и назвали — The Pyramids(рис.19). Сейчас в нем расположен Институт искусства Индианополиса.
Полуправильные многогранники в привычных вещах
Кресло Hedronics (рис.20) разработано известным немецким архитектором Даниелем Дендра (Баухаус) специально для недели российского дизайна Sretenka Design Week. В основе форм кресла лежит многогранник производный от плосконосого куба. Подобно оригами, кресло Hedronics выполняется из цельного листа металла и воплощает математическую гармонию строгих геометрических форм. Кресло может быть выполнено из цельного листа металла или из листа с декоративной перфорацией. Перфорированное кресло весит немного и выглядит наполненным воздушными пузырьками.

Рис.21
Всемирно известный художник и дизайнер из Дании Олафур Элиассон, выставка которого проходит сейчас в Tate Modern, создал новую световую инсталляцию Your Sound Galaxy (рис.21). Работа состоит из 27 многогранников, свисающих с потолка в виде двух концентрических кругов. Каждая объемная фигура снабжена светодиодом, который освещает пространство сквозь стыки составляющих частей многогранника.
Инсталляцию Your Sound Galaxy нельзя назвать такой прогрессивной и социально важной, однако она, как и многие другие работы Элиассона, выглядит очень загадочно и меняет пространство с помощью света.

Рис.22 Сравнение усечённого икосаэдра(слева) с футбольным мячом
Конструкция из этих 32 многоугольников называется усечённый икосаэдр(рис.22) — достаточно близкая к шару геометрическая фигура, компромисс между несферичностью и количеством швов на покрышке. Сферическая форма придаётся мячу за счёт давления воздуха, закачанного внутрь.
Рис.23
Флористы повинуясь законам математики создают гармоничные букеты на основе полуправильных многогранников(рис.23). На приведенной фотографии букет состоит из элементов двух типов: соприкасающихся крупных роз и заполняющих просветы мелких цветов. В такой форме букета угадывается усеченный додекаэдр, состоящий из 20треугольников и 12десятиугольников.
Ссылки на источники
- Каченовский М.И. Математический практикум по моделированию.-1959.-190с.
- Мотульский Р.С. Национальная библиотека Беларуси: новое здание – новая концепция развития / Национальная библиотека Беларуси. – Минск, 2007. – 322 с.
- Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия.-М.:МЦНМО, 2013 -272с
- Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия. Рабочая тетрадь №4. М.:МЦНМО, 2012 -88с
- Смирнова И., Смирнов В. Что такое «Полуправильный многогранник» Учебно-методическая газета «Математика».- 2007 .-№16-с.23-26
- Тиморин В.А. Комбинаторика выпуклых многогранников.-М.: МЦНМО, 2002.-16с.
- Geometryim.ru
- Arhimedgeom.ru
- Icosogeom.ru
- ru.wikipedia.org/

 А.
Б. Шишова
А.
Б. Шишова