Аннотация. Статья посвящена анализу методов прогнозирования графиков нагрузки энергосистемы. Авторы предлагают модель прогнозирования графиков нагрузки на основе разработанного нейро - нечеткого критика.
Ключевые слова: прогнозирование графиков нагрузки энергосистемы, регрессионные методы, нейросетевое прогнозирование, нейро-нечеткий критик.
Прогнозирование графиков нагрузки энергосистемы является важной задачей стратегического управления энергосистемами. На основе прогноза нагрузок определяют количество и мощность генерирующих источников, работающих в базовом и пиковом режиме, состав основного технологического оборудования, параметры характерных режимов. По прогнозу нагрузок также находят оптимальные режимы энергосистемы, выбирают состав работающего оборудования и распределяют резервы, рассматривают заявки на ремонт оборудования и дают соответствующее разрешение на его проведение.
Графики нагрузки энергосистем представляют последовательности наблюдений или расчетных значений, показывающих изменения мощности в течение определенного периода времени. В суточных, недельных и годовых графиках отображается периодичность процесса изменения мощности нагрузки, связанная с режимом работы людей, сменой дня и ночи, недельными циклами и сезонными изменениями в течение года.
Рассмотрим методы прогнозирования, нашедшие применение в данной задаче.
Традиционно для решения задач прогнозирования используются модели линейной и квадратичной регрессии. Это наиболее доступный и изученный тип моделей, позволяющих производить содержательную интерпретацию полученных результатов. Однако модели квадратичной регрессии используются в случаях, когда количество переменных модели не более 5. Модель линейной регрессии показывает хорошие результаты прогноза в случае «гладкого» временного ряда, если же в ряду наблюдается большая частота изменения знака и высокая амплитуда, то данная модель непригодна для прогнозирования. По данному методу производится прогнозирование одномерных временных рядов, которые не являются монотонно возрастающими или монотонно убывающими. Данные модели очень популярны среди аналитиков, не в последнюю очередь благодаря тому, что они встроены в программу Excel пакета MS Office и во все статистические пакеты.
Нейронные сети - это очень мощный и гибкий механизм прогнозирования. При определении того, что нужно прогнозировать необходимо указывать переменные, которые анализируются и предсказываются. Здесь очень важен требуемый уровень детализации. На используемый уровень детализации влияет множество факторов: доступность и точность данных, стоимость анализа и предпочтения пользователей результатов прогнозирования. В ситуациях, когда наилучший набор переменных неясен, можно попробовать разные альтернативы и выбрать один из вариантов, дающий наилучшие результаты. Обычно так осуществляется выбор при разработке прогнозирующих систем, основанных на анализе исторических данных.
Второй важный этап при построении нейросетевой прогнозирующей системы - это определение следующих трех параметров: периода прогнозирования Пn, горизонта прогнозирования Гп и интервала прогнозирования Ип. Период прогнозирования - это основная единица времени, на которую делается прогноз. Горизонт прогнозирования - это число периодов в будущем, которые покрывает прогноз. То есть, может понадобиться прогноз на 10 дней вперед, с данными на каждый день. В этом случае Пn= сутки, а Гп - 10 суток. Наконец, интервал прогнозирования - частота, с которой делается новый прогноз. Часто интервал прогнозирования совпадает с периодом прогнозирования. Выбор периода и горизонта прогнозирования обычно диктуется условиями принятия решений в области, для которой производится прогноз. Выбор этих двух параметров является едва не самыми трудным в нейросетевом прогнозировании. Для того чтобы прогнозирование имело смысл, горизонт прогнозирования должен быть не меньше, чем время, необходимое для реализации решения, принятого на основе прогноза. Таким образом, прогнозирование очень сильно зависит от природы принимаемого решения. В некоторых случаях, время, требуемое на реализацию решения, не определено, например, как в случае поставки запасных частей для пополнения запасов ремонтных предприятий. Существуют методы работы в условиях подобной неопределенности, но они повышают вариацию ошибки прогнозирования. Поскольку с увеличением горизонта прогнозирования точность прогноза, обычно, снижается, часто можно улучшить процесс принятия решения, уменьшив время, необходимое на реализацию решения и, следовательно, уменьшив горизонт и ошибку прогнозирования.
В некоторых случаях не так важно предсказание конкретных значений прогнозируемой переменной, как предсказание значительных изменений в ее поведении. Такая задача возникает, например, при предсказании момента, когда текущее направление движения рынка (тренд) изменит свое направление на противоположное.
Точность прогноза, требуемая для конкретной проблемы, оказывает огромное влияние на прогнозирующую систему. Также огромное влияние на прогноз оказывает обучающая выборка.
Первое, с чем сталкивается пользователь любого нейропакета - это необходимость подготовки данных для нейросети. На практике именно предобработка данных может стать наиболее трудоемким элементом нейросетевого анализа. Причем, знание основных принципов и приемов предобработки данных не менее, а может быть даже более важно, чем знание собственно нейросетевых алгоритмов. Последние, как правило, уже «зашиты» в различных нейроэмуляторах, доступных на рынке. Сам же процесс решения прикладных задач, в том числе и подготовка данных, целиком ложится на плечи пользователя.
Таким образом, построение нейросетевой модели прогнозирования обычно состоит из следующих этапов:
1 Выбор Пn, Гn, Иn;
2 Выбор значащих входов;
3 Проведение кросскорреляционного анализа выбранных входов и отсеивание сильно коррелирующих;
4 Сглаживание входов, в том числе заполнение пробелов в истории;
5 Структурный синтез нейронной сети, определяющий тип сети и метод обучения;
6 Параметрический синтез нейронной сети с помощью пакетного поиска лучшей модели на основе генетического алгоритма;
7 Прогнозирование на данных в точке актуальности. Проверка ошибки прогноза.
Алгоритм работы предлагаемой системы прогнозирования приведен на рисунке 1.
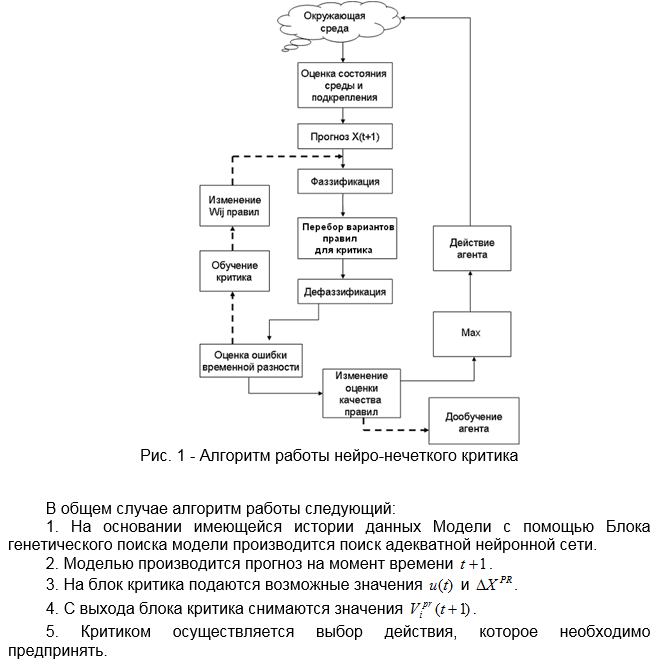
Разработанная нейро - нечеткая топология адаптивного критика позволяет обучить нейросеть на небольшом количестве примеров, а также дообучать (переобучать) в режиме реального времени по мере поступления новой информации без участия эксперта (впрочем, последний может корректировать процесс обучения). Нейро – нечеткая топология адаптивного критика может использоваться в случаях, когда невозможно построить точную модель среды, т. е. если среда недетерминирована. Графики нагрузок большинства подстанций удовлетворяют этому условию. Также данная топология является детерминированной и доступной для реализации на ПК.
Ссылки на источники
- Зуева В.Н. Обучение с подкреплением в нейронных сетях. Вестник СевКавГТИ: Научно-исследовательский журнал. Выпуск 14. - Ставрополь, с. 125-129, 2013.
- Зуева В.Н. Математическое обеспечение информационной системы учета и прогнозирования продовольственных ресурсов региона. Диссертация на соискание ученой степени кандидата технических наук / Краснодар, 2006

 В.
Н. Зуева
В.
Н. Зуева