Использование межпредметных связей на уроках математики в группах начального профессионального образования (НПО) для профессии «Станочник (металлообработка)»

Аннотация. Статья посвящена вопросам установления межпредметных связей между общеобразовательными предметами и дисциплинами специального цикла профессии «Станочник (металлообработка)»
Ключевые слова: межпредметные связи; математика; профессия «Станочник (металлообработка)» 

Преподавание математики в системе НПО должно опираться на нормативные документы, такие как «Стандарт среднего (полного) общего образования по математике» и «Федеральный компонент государственного стандарта среднего (полного) общего образования» [1].

Математическое образование в системе НПО занимает одно из ведущих мест, что определяется безусловной практической значимостью математики, её возможностями в развитии и формировании мышления человека, её вкладом в создание представлений о научных методах познания действительности. В процессе  преподавания математики следует показывать, что из абстрактных математических понятий строятся модели самой конкретной действительности, что общие законы математики применяются в различных областях практической деятельности. Процесс обучения математике в колледже желательно организовать так, чтобы вызвать у обучающихся стремление применять полученные знания, умения в новых условиях, действовать инициативно, добиваться осуществления поставленных задач, уметь отстаивать свою точку зрения, опираясь на собственные знания и жизненный опыт.

Достаточный уровень систематизации знаний студентов, может быть, достигнут только при осуществлении межпредметных связей, которые, способствуют формированию у студентов целостной научной картины мира, устанавливают связи в изучении основ наук с трудовой, политехнической и профессиональной подготовкой студентов.

Для всех профессий, осваиваемых в колледже, профессионально значимыми, в первую очередь, являются умения и навыки расчётного и вычислительного характера, умение выполнять действия с числами разного знака, оперировать обыкновенными и десятичными дробями, выполнять приближённые вычисления, делать прикидку ожидаемого результата, оперировать процентами, что требует также уверенного владения навыками работы на калькуляторе.

Студенты осваивающие профессию «Станочник (металлообработка)» на уроках специальных предметов активно используют отношение величин, пропорции, прямую и обратно пропорциональную зависимости, степень числа, решают уравнения, преимущественно линейные или приводящиеся к линейным.

Особую значимость в технических расчётах имеют тригонометрические соотношения в прямоугольном треугольнике, а при описании принципов работы различных механизмов (кривошипно – шатунного, индукторного) тригонометрические функции, умение преобразовывать и упрощать тригонометрические выражения, вычислять их значения, работать с графиками тригонометрических функций.

На уроках математики особое внимание нужно уделять операции перевода единиц измерения: для технических специальностей - сантиметров в миллиметры и наоборот; для гуманитарных и экономических – килограммы в граммы; рубли в копейки и наоборот.

Некоторые особенности применения межпредметных связей специальных предметов с математикой будут представлены на примере профессии «Станочник»

Для будущих станочников профессионально значимым является умение находить область определения и значения функций, знание свойств элементарных функций, умение строить и читать графики функций, т. к. язык функциональных зависимостей является базисным в соответствующей технической документации, применяемой на производстве.

В связи с широким применением на специальных  предметах и на производстве разнообразных измерительных инструментов обращается внимание при изучении математики на задачный материал, связанный с переходом от одних единиц измерения к другим.

Для осмысления и грамотного использования в профессиональной деятельности математических зависимостей рассматриваются на уроках математики пропедевтические задачи с соответствующим профессиональным содержанием. Станочники должны  уметь решать производственные задачи, связанные с планированием операций, с нахождением оптимальных решений (выбор технической последовательности, последовательности обработки, режима резания, определение минимального расхода материала) для чего используются дифференциальные исчисления и решение творческих задач.

При изучении, закреплении материала в курсе математики в системе НПО высокий результат даёт использование теоретических основ специальных предметов:

1)    В виде наглядных примеров:

Образцы применения теоретического материала при изучении курса «Математика» для профессии «Станочник»:

• В теме: «Векторы в пространстве» при рассмотрении вопроса «Прямоугольная система координат в пространстве» предлагается рассмотреть в горизонтально-фрезерных консольных станках расположение шпинделя (горизонтальное) и стола, который перемещается в трёх взаимно-перпендикулярных направлениях (продольное, поперечное и вертикальное) [2; 3];
• В теме: «Многогранники» при рассмотрении фигуры параллелепипед наглядным является рассмотрение процесса резанья, через силу резанья, которая проецируется на три выбранные оси – х; у и z (рисунок 1). При этом ось х совпадает с осью заготовки, ось у перпендикулярна оси х,  ось z направлена касательно к плоскости резания, тогда сила резания (R) является диагональю параллелепипеда, а её составляющие Р_х; Р_у; Р_z – его гранями [4].

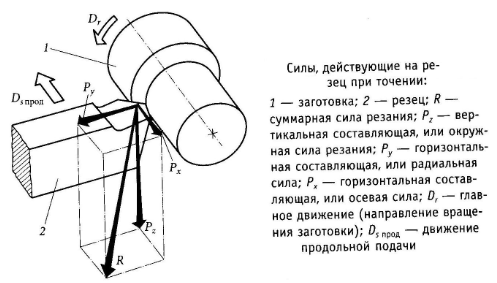
Рисунок 1: Силы, действующие на резец при точении

• При изучении тем: «Параллельность и перпендикулярность основных фигур в пространстве» обращают внимание на следующее, что при изготовлении детали контролируют перпендикулярность торцевой поверхности обработанной детали относительно её базовой поверхности и отклонение от параллельности плоских поверхностей, так же можно рассмотреть допуск параллельности (перпендикулярности) поверхности по условным обозначениям на чертежах.

Пример обозначения на чертеже допуска параллельности поверхности относительно поверхности А на 0,02 мм, представлен на рисунке 2:

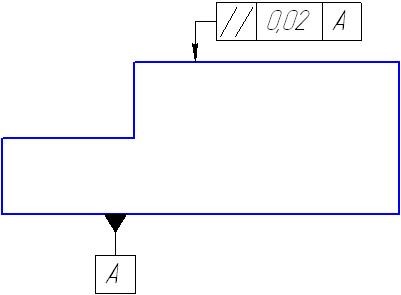 Рисунок 2

2)    При выполнении тестовых заданий:

Использование теоретического материала специальных предметов позволяет включать в тестовые опросы задания с профессиональной направленностью, что повышает интерес к математике и способствует всестороннему развитию студентов.
Образцы тестовых заданий с профессиональной направленностью: 

В теме «Тела вращения» включено задание: 

Конусность вала D = 40 мм, d = 34 мм, Н = 60 мм (рисунок 3) равна… 

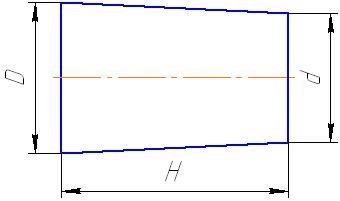       Рисунок 3

 а) 10 мм;   б)1 мм;    в) 0,1мм;     г) 0,6 мм 

В теме: «Перпендикулярность прямых и плоскостей» включено задание: 

Расшифруйте условное обозначение на чертеже рисунка 4:                               

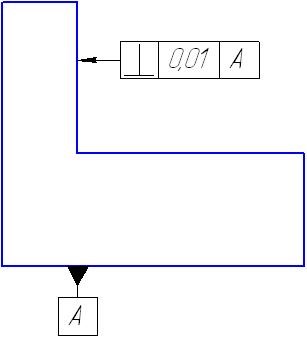Рисунок 4

а) допуск плоскости относительно поверхности А равен 0,02 мм;
б) допуск перпендикулярности поверхности А равен 0,02 мм;
в) допуск перпендикулярности поверхности относительно поверхности А равен 0,02 мм

В теме: «Математика в профессии» включены задания: 

• Определить припуск на обработку, глубину резания при обтачивании детали за один проход по следующему чертежу (рисунок 5):  

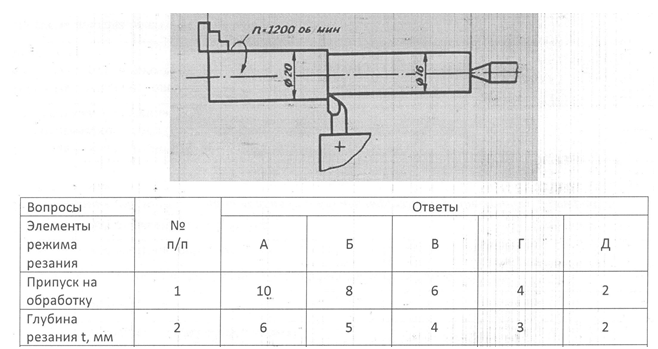
Рисунок 5

• Подсчитать необходимую частоту вращения шпинделя (об/мин) при сверлении отверстия D = 12 мм стальной детали, если скорость резания V_Т = 30 мм/об:

• Определить шаг резьбы (S) при нарезании трапецеидальной резьбы, если длина режущей кромки прорезного резца b = 2,04 мм по формуле:

 b = 0,34S

а) 2;   б) 4;  в) 5;  г) 6

 3)    при решении задач с профессиональной направленностью:

Большое внимание на уроках математики нужно обращать на задачи с профессиональной содержанием, решение которых позволяет увидеть тесную связь математики с предметами специального цикла и в тоже время студенты получают необходимые знания в соответствии с  обязательным минимумом.

Таблица 1

Задачи профильного содержания курса «Математика» для групп НПО

Достаточный уровень систематизации знаний студентов НПО может быть достигнут только при осуществлении межпредметных связей, которые  показывают целостность научной картины мира, устанавливают связи в изучении основ наук с профессиональной подготовкой студентов. На уроках математики студенты получают навыки логического аналитического мышления, развивают пространственное воображение и память, повышают уровень внимательности. Все эти навыки играют основополагающую роль при изучении специальных теоретических дисциплин и практическом применении полученных знаний в мастерских и на производстве. Владение математическим аппаратом позволяет успешно освоить профессиональные области знаний, особенно технические науки, и в дальнейшем стремиться к более высокому уровню образования и использованию современного оборудования.

Ссылка на источники

1.  Стандарт среднего (полного) общего образования по математике
2. Вереина Л. И. Фрезеровщик:  Оборудование и техническая оснастка: учебное пособие / Л. И. Вереина. – М.|: Издательский центр «Академия», 2008. – 64 с
3. Ганевский Г. М., Гольдин И. И.   Допуски, посадки и технические измерения в машиностроении: учебник / - М.|: Издательство «ПрофОбрИздат», 2004. – 288 с
4. Багдасарова Т. А.  Основы резания металлов: учебное пособие /Т. А. Багдасарова. –  М.|: Издательский центр «Академия», 2007. – 80 с