Аннотация. Статья посвящена исследованию теорем и закономерностей, происходящих на биллиардном столе. В работе использовано решение текстовых задач как на биллиардном столе, так и не только.
Ключевые слова: траектория,шар, переливание жидкости
Впервые о математическом базисе бильярдной игры заговорил Гаспар Густав Кориолис в своей книге «Математическая теория явлений бильярдной игры» в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа.
«Теория биллиардов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа с помощью биллиарда. Намного ближе общеобразованному читателю результаты исследований математиков Штейнгауза, Альхазена и Гарднера.
Как известно, в физике весьма подробно рассматриваются законы упругих тел, а также выводятся формулы, выражающие силу удара шаров, скорость после удара и т. д. Мы рассмотрим лишь движение шаров, которые имеют только поступательное движение. Отличий от обычного бильярда будет много: бильярдный стол не всегда прямоугольный, шар только один и нет ни луз, ни кия.
Согласно законам механики при отражении абсолютно упругого биллиардного шара от прямолинейного борта угол падения шара равен углу его отражения – закон упругого отражения.
Биллиардный шар будем считать точечным объектом. Таким образом, мы считаем, что биллиардный шар это движущаяся точка, и поэтому можно говорить о траектории биллиардного шара – о ломанной линии, по которой движется шар в соответствии с законом упругого отражения. Точки излома этой ломанной лежат на «бортах биллиардного стола». Мы будем рассматривать биллиардные столы произвольной формы.
Может случиться так, что при построении траектории проходящей через точку Р в направлении V, через некоторое время траектория пройдёт через ту же точку Р в том же направлении. Очевидно, что далее траектория опять пойдёт по тому же пути. Такая ситуация соответствует повторяющемуся периодическому движению биллиардного шарика. Отвечающие подобному движению траектории называются периодическими.[2]
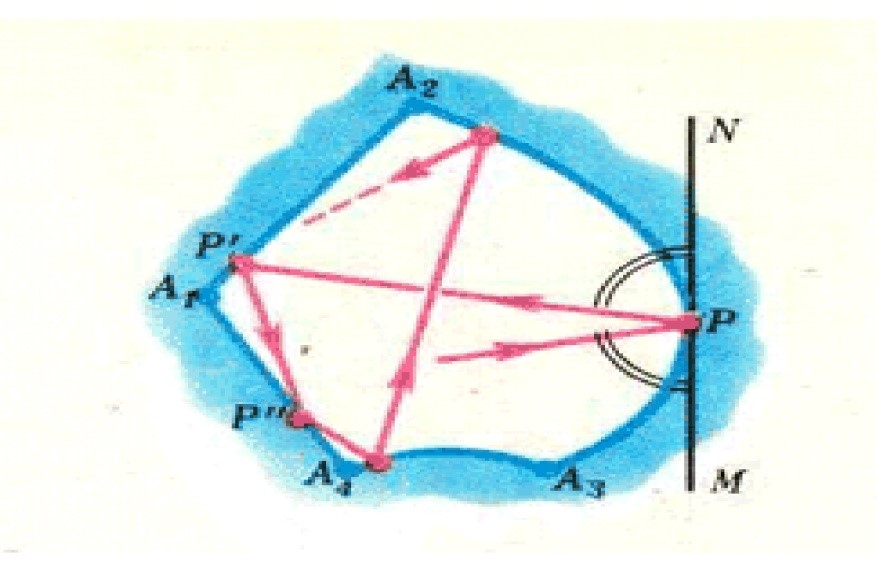
Рис. 1
Геометрически периодическая биллиардная траектория – это замкнутая вписанная в кривую Г ломаная, обладающая свойством «равенства углов падения и отражения».
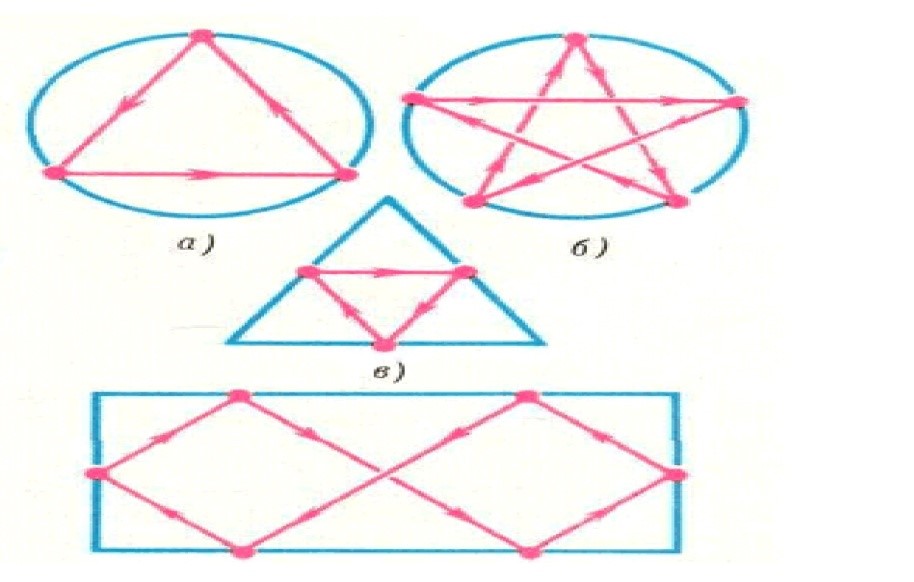
Рис.2
Теорема о биллиарде в круге.Рассмотрим биллиард в круге Q, описанном окружностью Г. Его траекторией являются вписанные в Г ломанные, обладающие свойством равенства углов падения и отражения. Из этих свойств следует, что все звенья траектории равны между собой, как равны друг другу и опирающиеся на их центральные углы.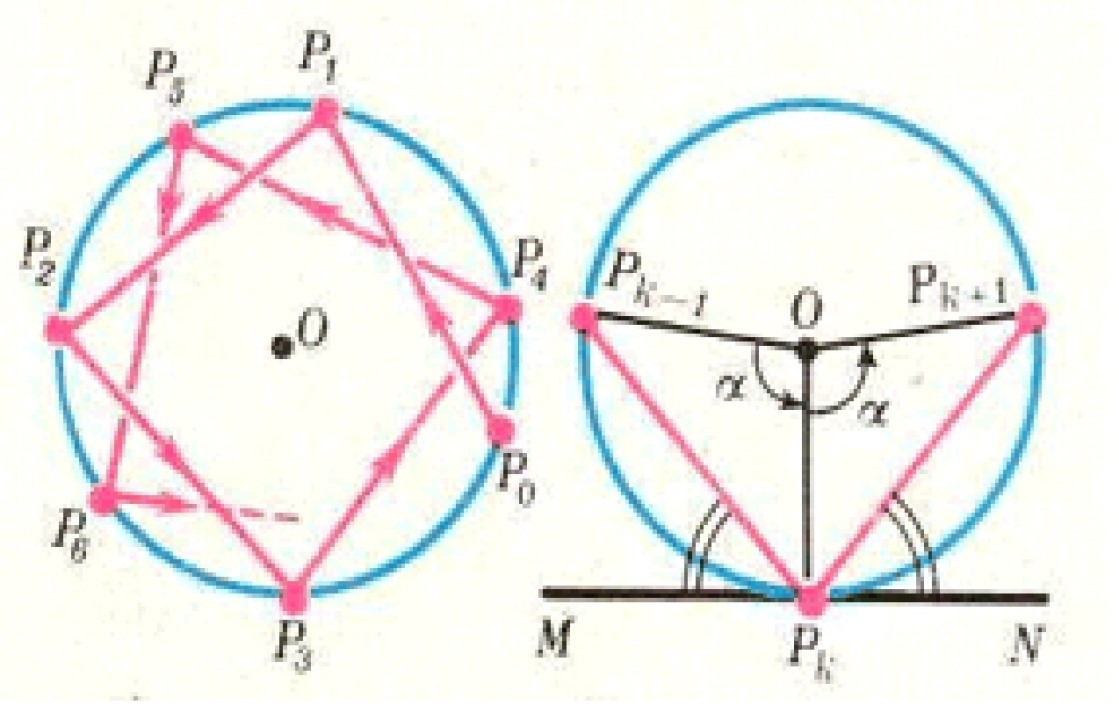
Рис.3
Вид биллиардной траектории в круге полностью измеряется числом α.
А)Если число α соизмеримо с 2π, то отвечающая α биллиардной траектории периодична.(Числа a и b называются соизмеримыми, если их отношение является рациональным числом, т.е. a/b=m/n, где m и n целые числа.)
Б)Если α/π иррационально, то траектория не периодична.
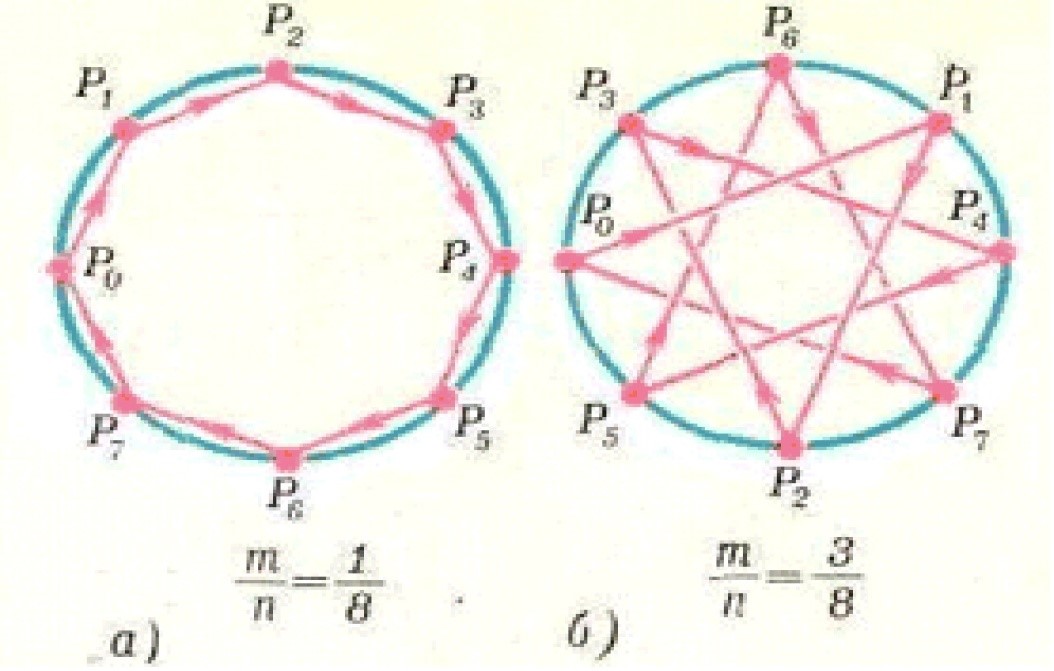
Рис.4
Доказательство:
a) Пусть α соизмеримо с 2 π; тогда α —(m/л)-2 π, где т и п — целые. Следовательно, п α =т 2 π, и поэтому при повороте около центра окружности на угол п α радиан каждая точка окружности переходит в себя. В частности, для вершин рассматриваемой траектории получаем:P(n)=P(n0), P(n+1)=P(1)... Таким образом, вершины траектории P(0)P(1)P(2)P(3) начиная с n-й, повторяются, т. е. траектория периодична.
Заметим, что если дробь m/n— — α/2 π несократима, то отвечающая α периодическая траектория — это замкнутая ломанаяP(0)P(1)...P(n-1)P(0) состоящая в точности из n звеньев. При m=l это будет правильный n-угольник, вписанный в окружность Г, а при m>2 траектория представляет собой правильную самопересекающуюся замкнутую (звездчатую) ломаную, вписанную в Г.
б) Рассуждая от противного, видим, что достаточно доказать следующее: если траектория P(0)P(1)P(2)... периодична, то α и π соизмеримы. Из периодичности траектории вытекает, что, начиная c некоторого номера n. вершины траектории повторяются: P(n)=P(0); P(n+1)=P(1)... Но это означает, что при повороте на угол п α радиан точка P(0) переходит сама в себя; следовательно, угол п α есть целое кратное полного угла: п α =m2 π. Таким образом: α/ π=2m/n
Итак, если α несоизмеримо с π, то отвечающая углу α биллиардная траектория есть незамкнутая ломаная P(0)P(1)P(2)... равными по длине звеньями, вписанная в окружность Г. Поскольку звенья этой ломаной равны по длине, их середины удалены от центра окружности Г на одинаковое расстояние, т. е. лежат на некоторой окружности Г(1), концентрической с Г. Все звенья рассматриваемой траектории касаются этой меньшей окружности Г(1) и траектория никогда не заходит внутрь т. е. целиком лежит в кольце К между окружностями Г(1) и Г. [3]
Рассмотрим ещё один способ применения биллиардного шара для решения задач.
Задача: имеются 2 ведра объёмом 7л и 11л и большая бочка с водой как с их помощью отмерить 2л воды?
Данную задачу можно решить перебором вариантов, но рассмотрим метод с применением биллиардного шара. Для решения задачи нам потребуется бумага с сеткой из равносторонних треугольников. Построим ромбоид с длинами сторон 7 и 11 единиц, и отметим на сторонах координаты точек. Поместим наш шар в точку с координатой (0;0) и будем пускать наш шар вдоль нижней стороны фигуры. Так наш шар попадёт в точку с координатой 11. Значит, 11-литровое ведро будет полное. Шар будет отражаться от бортов по закону упругого отражения. Так после отражения от стен он попадёт в верхний борт в точку с координатой 4. Это значит, что в 11-литровом ведре будет 4 литра воды. Будем рисовать так траекторию шара, пока на одном из бортов она не попадёт в точку с координатой 2. Так мы узнаем, в какой последовательности необходимо производить переливания. Сделав построение мы узнаем, что необходимый результат будет достигнут после 18 переливаний. Также решение будет получено, если изначально шар пустить вдоль верхней стороны. В таком случае потребуется 13 переливаний.
Требуется немного сообразительности, чтобы применить метод отражающегося шара к любой задаче о разливании жидкости.[1, с.496]
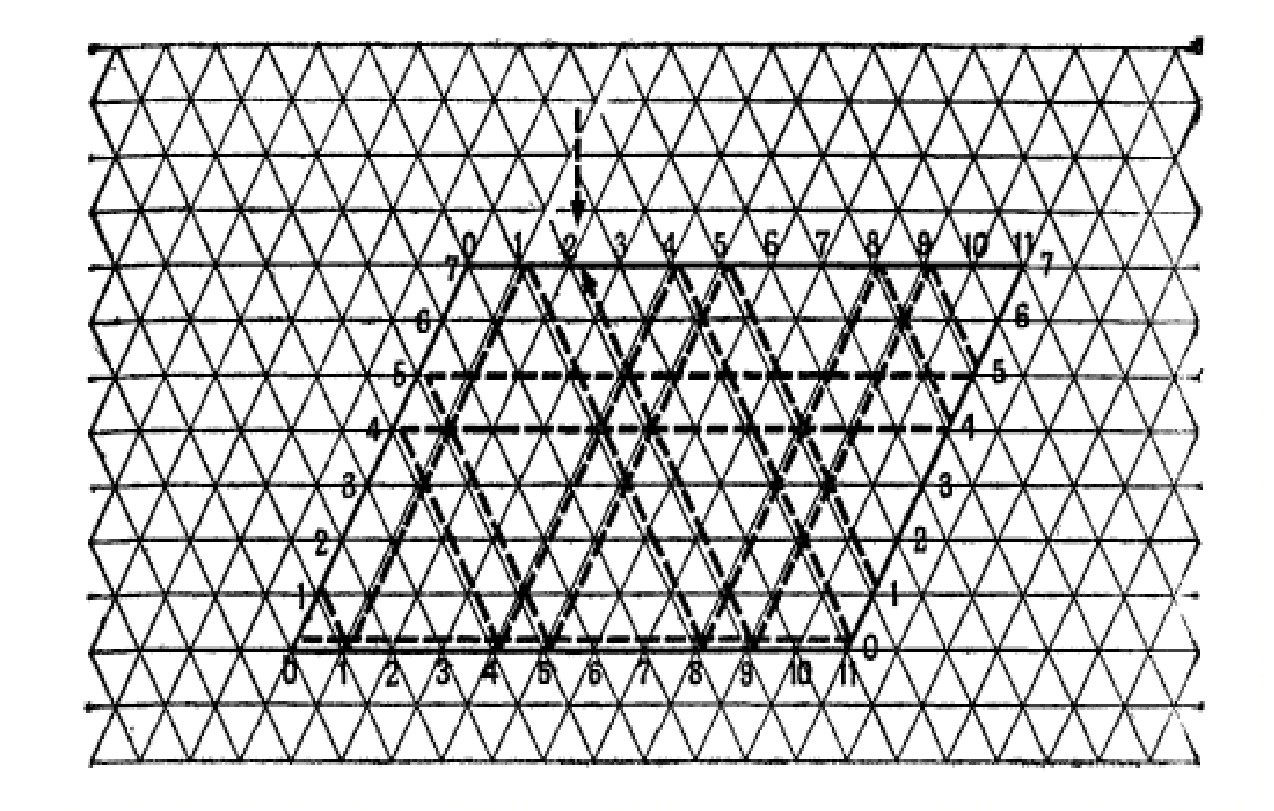
Рис.5
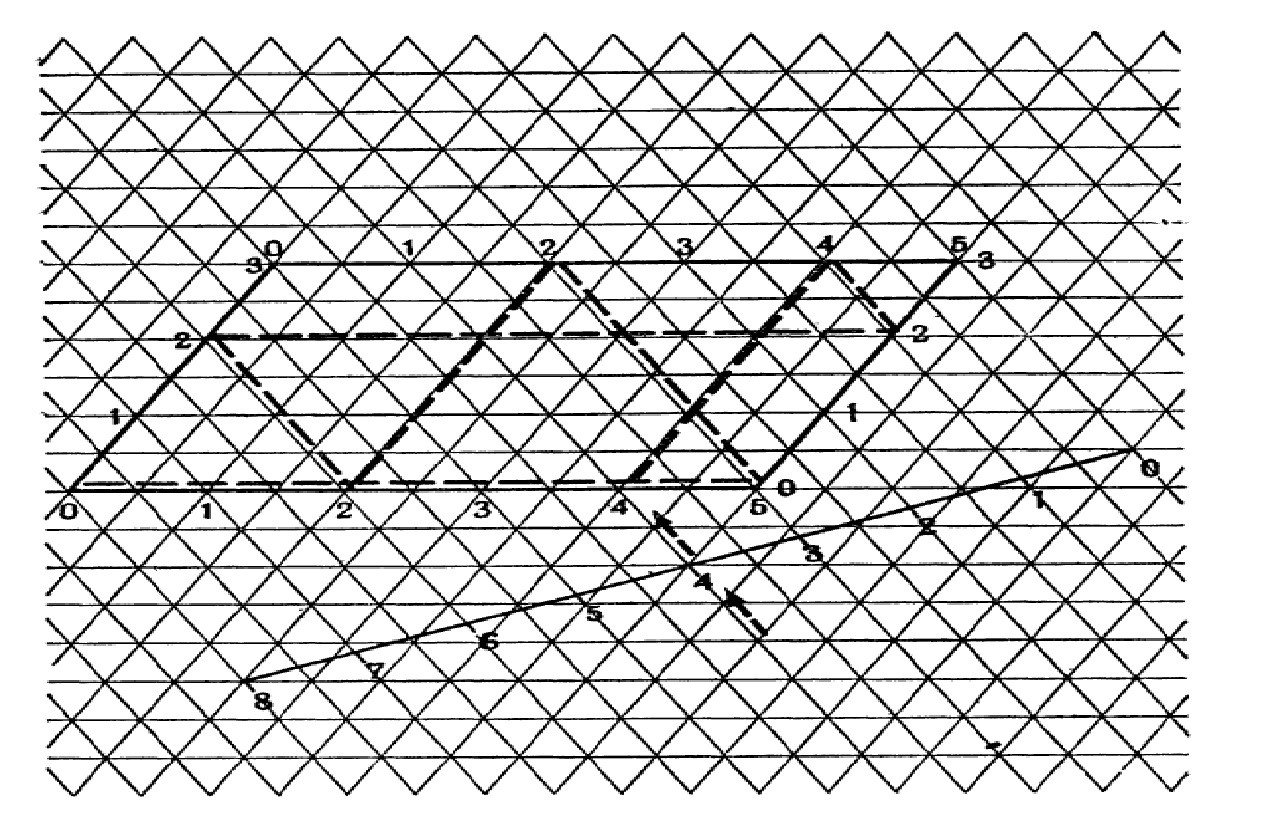
Рис.6
Можно заключить, что применение математики и физических моделей может не только помочь решить многие задачи, но и головоломки.
Ссылки на источники
- Гарднер М.Г20 Математические досуги. Пер. с англ. Ю.А.Данилова. Под ред. Я. А. Смородинского. М., «Мир», 1972. 496 стр. с илл.
- Журнал «Квант» №3 1989г.
- Журнал «Квант» №9 1979г.

 А.
А. Арасланов
А.
А. Арасланов