Аннотация. Статья посвящена вопросам разработки режимов работы светофорного регулирования с помощью нечеткого моделирования с целью предотвращения образования заторов.
Ключевые слова: транспортное средство, улично-дорожная сеть, затор, нечеткое моделирование, лингвистическая переменная, функции принадлежности.
В связи с ростом автомобилизации все сложнее становится управлять транспортными потоками, в результате образуются заторы. В городах с исторически стожившейся застройкой применять некоторые мероприятия не представляется возможным. На сегодняшний день существует ряд мероприятий по снижению заторов. Распространенными из них являются: ограничения на въезд в центр города, ограничения на парковки, привилегии для общественного транспорта и др.
В результате исследований и практического опыта в данной области разработаны комплексные мероприятия по улучшению сложившейся ситуации на улично-дорожной сети (УДС), которые являются наиболее эффективными.
К основным таким мероприятиям по снижению заторов относятся:
¾ строительство УДС (строительство объездных дорог, многоуровневых развязок, надземных и подземных переходов, внеуличных стоянок и парковок, паркингов) [1, 2];
¾ снижение интенсивности движения путем введения платных парковок и стоянок, полный запрет стоянки, повышение привлекательности маршрутно-пассажирского транспорта, автоматические системы контроля въезда на дворовые территории [3, 4, 5, 6];
¾ оптимизация использования существующей УДС (введение одностороннего и реверсивного движения, выбор оптимальных схем и алгоритмов объектов светофорного регулирования, изменение плана перекрестков, разработка и внедрение АСУДД (автоматизированной системы управления дорожным движением) и ИТС (интеллектуальной транспортной системы)) [7, 8].
Некоторые из приведенных мероприятий являются дорогостоящими и имеют длительный период окупаемости (строительство УДС), а такие как выбор оптимальных алгоритмов объектов светофорного регулирования особых затрат не требуют, но при определенных условиях исчерпывают свою эффективность, аналогично как и производительность УДС снижается при определенной интенсивности.
Для того, чтобы снизить возникновение заторовых ситуаций на УДС городов на регулируемых перекрестках и перегонах можно использовать нечеткое моделирование.
Впервые идеи теории нечетких множеств были предложены более 35 лет назад американским математиком Лотфи Заде. Эта теория позволяет описывать качественные, неточные понятия, а также знания об окружающем мире, оперировать полученными значениями с целью получения новой информации. Методы построения информационных моделей значительно расширяют традиционные области применения компьютеров и образуют независимое направление научно-прикладных исследований. Такое направление получило название – нечеткое моделирование.
В последнее время нечеткое моделирование все чаще является наиболее используемым и перспективным направлением прикладных исследований в области управления и принятия решений. Нечеткое моделирование становится особенно важным и полезным, когда в описании технических систем и бизнес-процессов присутствует неопределенность, которая затрудняет или исключает применение точных количественных методов и подходов.
Нечеткое моделирование при управлении техническими системами позволяет получать более адекватные результаты по сравнению с результатами, которые основываются на использовании традиционных аналитических моделей и алгоритмов управления. Нечеткие методы имеют широкий диапазон в своем применении, с каждым годом охватывая различные области знаний.
Также нечеткая логика, служит основой для реализации методов нечеткого управления, более естественно описывает характер человеческого мышления и ход его рассуждений, чем традиционные формально-логические системы. Именно поэтому изучение и использование математических средств для предоставления нечеткой исходной информации позволяет строить модели, которые наиболее адекватно отражают различные аспекты неопределенности, постоянно присутствующей в окружающей нас реальности [9].
Разработка и применение систем нечеткого вывода включает в себя ряд этапов, реализация которых выполняется с помощью основных положений нечеткой логики [10].
1. Фаззификация: разработка процедуры перехода от четких значений входных переменных к нечетким. Выбор вида и взаимного расположения функции принадлежности (ФП) входных лингвистических переменных.
2. Формирование структуры базы правил: разработка согласованного множества связей входы-выход регулятора.
3. Агрегирование: разработка процедуры определения степени истинности условий по каждому из правил.
4. Активизация: разработка процедуры определения степени истинности заключений по каждому из правил.
5. Аккумуляция: разработка процедуры объединения степеней истинности заключений по всей базе правил.
6. Дефаззификация: разработка процедуры перехода от нечеткого значения выходной переменной к четкому.
Для получения оптимальных режимов работы светофорного регулирования необходимо рассмотреть три входных лингвистических переменных для фаззи-регулятора, образующих входной вектор β = [β1, β2, β3], и одна выходная лингвистическая переменнаяβ4,
гдеβ1 – количество транспортных средств(ТС);
β2 – темп изменения количества ТС;
β3 – коэффициент сцепления шин с поверхностью дороги;
β4 – длительность разрешающего сигнала.
Целесообразно для предполагаемой системы нечеткого вывода использовать ФП нечетких лингвистических переменных в виде трапеций или треугольников. Данный выбор обусловлен простотой расчета ФП и высокой эффективностью программной реализации [11]. Трапециевидные ФП используются для характеристики лингвистических переменных на границах диапазона ее изменения, а в остальных случаях используются треугольные ФП. Каждая трапециевидная ФП задается вектором из четырех значений, которые соответствуют абсциссам вершин трапеции. Например, ФП F2 = [f1, f2, f3, f4]. По аналогии формируется треугольная ФП F1 = [f5, f6, f7]. Пример реализации треугольной и трапециевидной ФП представлен на рисунке 1.
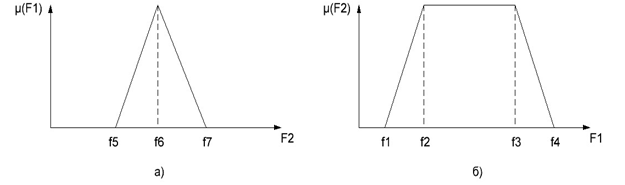
Рисунок 1 - а) треугольная ФП; б) трапециевидная ФП
Приведем пример для первой лингвистической переменной β1,значения которой определены из статистических данных.
- VS (Very Small) – «очень малое» [0, 10];
- S (Small) – «малое» [8, 19, 30];
- M (Medium) – «среднее» [28, 43, 58];
- B (Big) – «большое» [56; 63; 70];
- VB (Very Big) - «очень большое» [68; 86].
На рисунке 2 представлены ФП для лингвистической переменной β1 «Количество ТС».
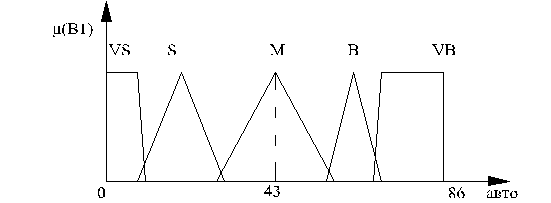
Рисунок 2 - Функции принадлежности для лингвистической переменной
β1 «Количество ТС»
Оставшиеся входные и выходная переменные определяются аналогично. Далее формируем базу нечетких правил.
В качестве примера приведем три характерных правил нечеткого вывода:
1) ЕСЛИ β1 = VS И β2 = NB И β3 = S ТО β4 = VS;
2) ЕСЛИ β1 = S И β2 = PS И β3 = NB ТО β4 = M;
3) ЕСЛИ β1 = B И β2 = Z И β3 = B ТО β4 = B.
Формирование поверхности нечеткого вывода для разработанной нечеткой модели β4 «Длительность разрешающего сигнала» реализуется в системе Matlab.
Для реализации системы нечеткого вывода в среде Matlab имеется спе-циальный пакет Fuzzy Logic Toolbox.
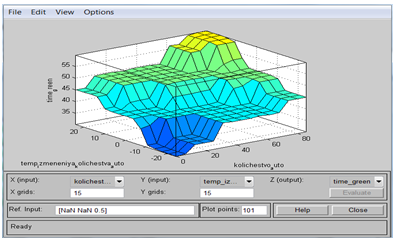
Рисунок 3 - Поверхность нечеткого вывода
Таким образом, задачу получения управляющего сигнала для светофорного объекта можно решить, используя систему нечеткого вывода. Представленная на рисунке 3 поверхность нечеткого вывода позволяет установить зависимость значения выходной переменной β4 от значений входных переменных β1, β2 и β3 нечеткой модели системы управления светофорным объектом. Данная зависимость может быть основой для программирования контроллера или аппаратной реализации соответствующего нечеткого алгоритма управления в форме таблицы решений.
Ссылки на источники
- Грекова О., Лекарство от затора. Что такое хорошо и что такое «пробки»?/ О. Грекова, Е. Егорова, Д. Кафанов //Московский Комсомолец. – 2003. – 10 октября.
- Грекова, О. Транспортные проблемы и их решение / О. Грекова // Мир дорог. – 2005. – 15 марта.
- Гай Л.Е., Кущенко С.В., Загородний Н.А. Технические средства управления стоянкой транспортных средств как один из способов организации движения / Л.Е. Гай, С.В. Кущенко, Н.А. Загородний // Организация и безопасность дорожного движения: материалы IV Всероссийской научно-практической конференции, Тюмень.: ТюмГНГУ, 2013. – С. 38-41.
- Демин А., Чтобы избежать заторов на дорогах / А. Демин // Транспорт России. – 2014. – №11 Еженедельник «Аргументы и Факты», 2014. – № 49.
- Кущенко С.В., Повышение эффективности организации движения на основе моделирования транспортных потоков: дис. ...канд. техн. наук: 05.22.10 /Кущенко Сергей Викторович. – Орел, 2012. – 133 с.
- Дацюк А.М., Автоматизированная система управления дорожным движением (АСУДД) в Санкт-Петербурге / А.М. Дацюк, С.И. Саблин // Организация и безопасность дорожного движения в крупных городах: сб. докл. шестой междунар. научно-практ. конф. – СПб: Научно-образовательный центр БДД при АДИ СПбГАСУ, 2004. – С. 175-181.
- Печерский М.П., Общегородская автоматизированная система управления дорожным движением в г. Москва (система «СТАРТ» и ее дальнейшее развитие) / М.П. Печерский //Организация и безопасность дорожного движения в крупных городах: сб. докл. шестой международн. научн. - практ. конф. – СПб: Научно-образовательный центр БДД при АДИ СПбГАСУ, 2004. – С. 169-173.
- Леоненков А.В., Нечеткое моделирование в среде MATLAB и fuzzy TECH / А.В. Леоненков. СПб.: БХВ - Петербург, 2005 – 736 с.
- Деменков, Н.П. Нечеткое управление в технических системах: учебное пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 200 с.
- Юдин Д.А., Автоматизированная система управления вращающимися печами с применением технического зрения: дис. … канд. техн. наук: 05.13.06 / Юдин Дмитрий Александрович. – Белгород, 2014. – 169 с.

 Л.
Е. Кущенко
Л.
Е. Кущенко