Статистический анализ величин пробега автобусов ПАЗ-3205 при оценке коррозионно-усталостного разрушения их кузова

Аннотация. Рассмотрено влияние на жизненный цикл кузова автобуса времени эксплуатации и пробега предлагается провести ряд математических операций, в последовательности, состоящей из семи этапов. В данной статье автором проведен статистический анализ значений пробегов автобусов на результаты измерений в зонах, подверженных коррозии.
Ключевые слова: автобус, кузов автобуса, пробег, коррозия, разрушение, прочность.

Для рассмотрения влияния процессов коррозионно-усталостного разрушения [1] на прочность кузовов автобусов предлагается выполнить статистический анализ величин пробегов и сроков эксплуатации автобусов по результатам замеров площадей разрушенных участков и на их основе разработать математическую модель, реально отражающую коррозионные процессы, происходящие на деталях, узлах и сборочных единицах.

Разработку пространственно-временной модели процесса коррозионно-усталостного разрушения деталей, узлов и сборочных единицах подоконного и нижнего обвязочного поясов кузовов произведем для автобусов марки ПАЗ-3205, эксплуатировавшихся на территории Ростовской области.

При проведении исследований необходимо оценить зависимости значений общей площади подоконного бруса и нижнего обвязочного пояса кузовов, поврежденных коррозионно-усталостным разрушением, от пробега Х₁, тыс. км и срока эксплуатации Х₂, год, по предлагаемой форме (таблица 1).

Для рассмотрения влияния на срок службы кузова автобуса времени эксплуатации и километров пробега предлагается провести серию математических операции, в последовательности, состоящей из семи этапов [2]. В настоящей работе рассмотрим первый этап – статистический анализ величин пробегов кузовов автобусов ПАЗ-3205.

Для изучения закона распределения была рассмотрена выборочная совокупность из n=45 опытов в широком спектре возможных значений (таблица 1). С помощью команд пакета Maple 9.5 [3] были написаны программы для статистических исследований в форме научного блокнота.

Для полученной по результатам расчетов выборочной совокупности величин пробегов был составлен статистический ряд. Количество разрядов статистического ряда вычисляется по правилу Штюргеса [4]:

здесь: [X] – операция вычисления целой части числа.

Таким образом, при выборочной совокупности n=45 количество интервалов статистического ряда равно: k = 5. Границы разрядов статистического ряда с частотами выборочных значений, попавших в соответствующий разряд, запишем в виде таблицы 2.

Таблица 2

Статистический ряд для величин пробегов автобусов

Графическое изображение статистического ряда (гистограмма) представлена на рисунке 1. Вдоль горизонтальной оси на рисунке 1 отложены границы разрядов статистического ряда, а вдоль вертикальной оси – относительные частоты, деленные на шаг.

Здесь m_j – количество выборочных значений (таблица 2), попавших в j–й разряд, j=1,2,…5;

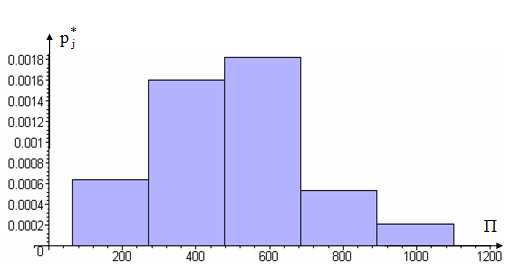
Рисунок 1 – Гистограмма величин пробегов кузова автобусов ПАЗ-3205

Выборочное среднее является состоятельной, несмещенной и эффективной оценкой для математического ожидания гипотетического закона распределения. Выборочное среднее указывает на среднее значение пробегов автобуса по результатам обследований.

По виду гистограммы и значениям коэффициентов асимметрии и эксцесса можно выдвинуть гипотезу о нормальном законе распределения. Описание основных параметров этого распределения и вид соответствующей функции плотности приводится в [4].

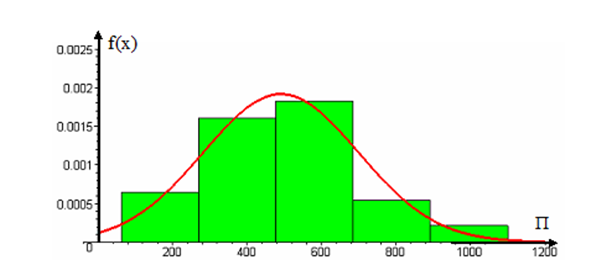
Рисунок 3 – Гистограмма пробегов автобусов и гипотетическая функция плотности нормального распределения

Из полученного закона распределения пробегов автобусов [5] следуют выводы:

– около 70% исследуемых эксплуатируемых автобусов имеют пробег 300-700 тыс. км и примерно по 15% - ниже и выше данного интервала;

– распределение автобусов по пробегу близко к нормальному, поэтому для статистического анализа применимы теоремы и правила, характерные для теории вероятностей в отношении нормального распределения.

Ссылки на источники

1. Семенова И.В. Коррозия и защита от коррозии / И.В. Семенова, Г.М. Флорианович, А.В. Хорошилов; под ред. И.В. Семеновой. – М. : ФИЗМАТЛИТ, 2002. – 336 с.
2. Овчинников Н.А., Суржик И.В. Оценка влияния коррозионно-усталостного разрушения на прочность кузова автобуса марки ПАЗ-3205 / Наука и инновации в области сервиса автотранспортных средств и обеспечения безопасности дорожного движения = Science and innovations in the field of vehicle service and traffic safety : междунар. сб. науч. трудов. - Шахты: ИСОиП (филиал) ДГТУ, 2014. – С 100-102.: ил.
3. Дьяконов В.П. Maple 9.5/10 в математике, физике и образовании / В.П. Дьяконов. – М.: СОЛОН-Пресс, 2006 – 720 с.
4. Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. – М.: Высшая школа, 1999. – 480 с.
5. Калмыков Б.Ю., Высоцкий И.Ю., Овчинников Н.А. Предложения по оценке прочности конструкции пассажирских транспортных средств / Инженерный вестник Дона. 2012. № 2. С. 7.