С.
Н. ФилипповаС.Филиппова
Мы живём в сложное время, когда молодые люди подвергаются негативному влиянию с одной стороны различных видов пропаганды: телепередач с цинично извращенной историей нашего отечества, откровенно пошлых Интернет сайтов, брутальных, а порой и просто низменных по содержанию и исполнению песен, танцев, влиянию на сознание различных тотальных сект, магии, сатанизма, идей фашизма, национализма, а с другой стороны - бытовой неустроенности, нищеты, частого пьянства и скандалов в неблагополучных семьях, губительной активности наркодилеров, преступному склонению несовершеннолетних подростков к проституции и т.п.
Что всему этому можем и должны противопоставить мы – учителя, преподаватели и воспитатели образовательных учреждений? И всё ли мы делаем для того, чтобы обучать и воспитывать достойных, высоко духовных, нравственно защищённых от отрицательного влияния окружающей среды, будущих граждан России? Вопросы животрепещущие, ведь какой будет наша молодёжь, таким и будет наше будущее! К большому сожалению, мы часто опаздываем отвечать на эти и многие другие вызовы времени, а порой и сами просто не готовы для убедительного противостояния.
Пришло время объединить усилия всех педагогических работников, общественности для выработки стратегии совместной деятельности по формированию духовных качеств наших воспитанников, возрождению морально-нравственных ценностей личности.
Конечно же, духовно – нравственное воспитание молодёжи во многом зависит от личности самого педагога, от силы его воздействия на ученика. Учительская стезя непроста, и счастье уже в том, что православным педагогам, есть у кого учиться, в ком черпать силы для милосердия душевной щедрости и доброты, без которых невозможен учительский труд. Мы призваны научить наших детей, прежде всего умению любить: любить свою семью, родных и близких людей, свой город, землю на которой живём, своё отечество. Там, где любовь, там и сердце человека, там и он сам! Нести свет знаний через любовь – главная задача педагогического труда. Ведь без любви всё есть – ничто. Обязанность без любви делает человека раздражительным, а справедливость без любви становится жестокостью. Правда без любви пахнет критиканством. Ум без любви преобразуется в хитрость. Власть без любви есть тирания. Бережливость без любви становится жадностью. Вера без любви превращается в фанатизм. Жизнь без любви наполнена холодом и пустотой. Есть только одна преобразующая сила – любовь! И величайший учитель человечества - Иисус Христос наполняет нашу жизнь особым содержанием, изменяет нас к лучшему, учит моральной чистоте, дает пример любви к человеку, беззаветному служению своему делу, самопожертвованию. «Только Бог заполняет вакуум в сердце человека через Сына своего Иисуса Христа», - говорил французский философ математик Блез Паскаль. И этот сердечный свет любви мы должны передавать нашим ученикам на каждом уроке, зажигая их сердца любознательностью, пробуждая совесть, воспитывая трудолюбие.
Рассматривая математику как фундаментальную общеобразовательную дисциплину со сложившимся содержанием и требованиями к подготовке обучающихся, выделяем следующие направления по воспитанию духовно – нравственных ценностей личности:
- формирование представлений об идеях и методах математики как универсальном языке науки на основе глубинных исторических и содержательных связей с христианскими понятиями нравственности и духовности, когда по словам Кеплера «…математические законы выступают зримым выражением божественной воли»;
- развитие интеллектуальных качеств личности, её культуры через расширение понятий о духовной составляющей изучаемого на уроках учебного материала. «Первый глоток из сосуда естественных наук порождает атеизм, - говорил Гейзенберг, - но на дне сосуда ожидает Бог»;
- расширение мотивационного поля интересов обучаемого к систематическим занятиям математикой с ориентацией на прикладную составляющую, то есть применение законов идеального мира к исследованию мира реального, где согласно Писанию: «Бог расположил всё мерою, весом и числом»
А теперь подробнее. Христианство, помещая человека между Богом и тем миром, который не есть Бог, требует от человека усилия по прорыву, Бог творит, а человек преображает мир «деланием» и только очистив себя, постигает контуры мироздания, становясь инструментом, функцией законов бытия. Одно из фундаментальных математических понятий функциональной зависимости, функции как закона, по которому каждому х из области определения ставится в соответствие один у, из множества значений несёт в себе глубокий этический смысл - «Послушание». Именно так можно назвать функцию - «Послушанием». Мир не может сам себе предписывать законы, как не может локомотив, едущий по рельсам, сам себе эти рельсы устанавливать. Законосообразность мирового движения, его рациональность и гармония заставляют предположить наличие Расписания. Концепция Провидения как закона управляющего природой и обществом против того, что всё в природе есть результат случайных соединений движущихся частиц материи. Даже математическая теория вероятностей находит свои закономерности в массовых случайных событиях, определяя вероятность случайного события. Изучая незримые законы математики, мы изучаем, тем не менее, видимый мир. Учёными двигает ВЕРА в то, что мир идеального воплощён в нашем мире. И именно ВЕРА является тем общим фундаментом, на котором стоит религия и строится математика. Действительно, духовное единение с Богом происходит через веру в существование Бога, когда образ жизни верующего соответствует догматам и заповедям христианства. В основе же математики (например, геометрии), лежат первичные неопределяемые понятия (точка, прямая, плоскость и т.д.), которые не существуют в окружающей нас реальности. Тем не менее, они связанны между собой свойствами – аксиомами, которые принимаются без доказательств, на веру и служат фундаментом построения геометрии. Таким образом, самая точная наука опирается на веру в правильность принятых аксиом. Аксиоматический метод стал важным научным инструментом познания мира. Большинство направлений современной математики, теоретической механики, ряде разделов современной физики, естествознания строятся на основе этого метода, который даёт законченное, логически стройное построение научной теории. В школе мы изучаем геометрию Евклида (||| век до н.э.). Существуют и другие геометрии Лобачевского, Римана, отличающиеся от традиционной аксиомой параллельности (V постулатом). Знакомство обучаемых с нравственными параллелями для фундаментальных математических понятий способствует формированию отношения к математике, как к части общечеловеческой культуры.
Движение, переменные величины и их взаимосвязи окружают нас повсюду. И когда математики сумели изучить взаимосвязь переменных величин, положив в основу категорию «становления» (дифференциальное исчисление), тем самым создав математический анализ как метод описания переменных величин и их взаимосвязей, тогда произошёл невиданный скачок в развитии научного мировоззрения. В наши дни без математического анализа невозможно не только рассчитать космические траектории, работу ядерных реакторов, бег океанской волны и закономерности развития циклона, но и экономично управлять производством, распределением ресурсов, организацией технологических процессов, прогнозировать течение химических реакций или изменения численности различных взаимосвязанных в природе видов животных и растений, потому что всё это – динамические процессы. Один из создателей дифференциального и интегрального исчислений И.Ньютон в переписке с проповедником Бейтли говорил: «Когда я создавал Трактат, я всё время имел в виду такие принципы, которые приемлемы для верующего человека, и ничто не может обрадовать меня больше, нежели удостовериться в таковой их пригодности». Именно открытие математического анализа в ХVІІ веке, в частности - исчисление бесконечно малых величин, явилось подтверждением правильности Декрета 1439г., в котором Флорентийский Собор установил, что «Вещество хлеба превращается в Тело Христово и вещество вина – в кровь Христову однако так, что весь Христос содержится под видом хлеба и весь под видом вина». Речь идет о том, что верующий причащается не частью тела Христова, он приемлет его целиком - как бы ни была мала частица облатки, вкушаемой им. Полнота сообщаемых даров не зависит от внешнего количества пресуществляемого хлеба. И вопрос средневековых схоластов об «ангелах» на кончике «иглы» не столь наивен, ибо это вопрос об исчислении бесконечно малых величин – так называемых «бестелесных духов». И как тут не вспомнить признание создателя кибернетики Норберта Винера: «Вера Христова не во вражде с истинным знанием, потому что не в союзе с невежеством». Обращая внимание студентов на тот факт, что в каждой маленькой молекуле организма человека заложен весь его генетический код, делаем выводы, что каждый его поступок, каждая мысль формируют будущее. Чистота помыслов и действий - основа счастливой и успешной жизни.
Не менее интересными, на наш взгляд, представляются некие параллели между религией и математикой, которые можно проводить на уроках математики.
Наука, как и вера, познает мир невидимый, ведь «…в науке чистое мышление пытается познать скрытую гармонию мира», - писал В.Гейзенберг. Откуда эта гармония абстрактно-логических математических построений? Изобретает математик или открывает? Несомненно, изобретает, творит, а не просто находит зависимости и формулы во внешнем мире. Ещё древние греки рассматривали постижение математических дисциплин как сложный процесс самого высокого духовного ранга. Научный поиск сродни духовному поиску, если им занимается духовный человек. Великий Эйнштейн говорил: «В наш материалистический век серьёзными учеными могут быть только глубоко религиозные люди…». И ещё одна параллель, поговорим о чудесах, хотя особый интерес к ним не всегда оправдан. Православие настаивает на сдержанном, трезвом отношении к таинственным явлениям, ведь «чудеса» могут быть и чёрными. Но главным чудом, положившим начало самой христианской религии, было воскресение - Иисуса Христа. Ежегодно сотни миллионов верующих с трепетом ожидают схождение Благодатного Огня на Гроб Господень в Иерусалиме в канун православной Пасхи. С этим великим чудом трудно что-то сравнивать, однако в математике есть свои, не столь значимые, но всё же чудеса. Так например, существование иррационального ( дословный перевод – не постигаемый разумом) числа «е», которое можно только приблизительно вычислить, какпредел последовательности 
при бесконечном возрастании п (е=2,718…). И тут начинается невероятное – таким абстрактным образом полученное число, нередко появляется там, где его не ждут и начинает играть огромную роль не только в самой математике, но и в физике, астрономии и др. науках. Вот некоторые вопросы, при математическом рассмотрении которых приходится пользоваться этим числом: барометрическая формула (уменьшение давления с высотой), закон охлаждения тел, радиоактивный распад и возраст Земли, колебания маятника в воздухе, формула Циолковского для скорости ракеты, колебательные явления в радиоконтуре, биологический рост клеток и т.д. А разве не чудо, что по логарифмической спирали свёрнуты раковины многих улиток и моллюсков, а также паук эпейра сплетая паутину, скручивает нити вокруг центра по логарифмической спирали, рога горных козлов – архаров, закручены по логарифмической спирали и по логарифмическим спиралям закручены многие галактики, и в частности галактика, которой принадлежит наша солнечная система.
Жизнь, особенно интеллектуальная, по мнению Пуанкаре, возможна лишь потому, что в мире существуют определённые закономерности. Математика же занимается классификацией и изучением любых закономерностей, которые могут быть познаны. Закономерность – это наиболее стабильная характеристика постоянно меняющегося мира. Например, закономерность, которую математики обозначают как
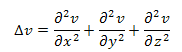
- результат применения оператора Лапласа к некоторой функции, выражаемый через вторые частные производные по координатам, когда = 0 . Она возникает в связи с такими явлениями, как гравитация, свет, звук, теплота, магнетизм, электростатика, электрический ток, электромагнитные излучения, морские волны, полёт самолёта, колебания упругих тел и строение атома, не говоря о чисто математической теории функций комплексного переменного. Физически применения этой закономерности различны, математически - одинаковы. Мы столкнулись с понятием - изоморфный, т.е. «имеющий одну и ту же форму», когда одна теория имеет 12 применений. Возникает вопрос: Чем вызвано то, что эта закономерность встречается так часто? Окончательного ответа нет, и даже если мы докажем, что эта закономерность имеет ряд свойств, делающих её особенно подходящей; но тогда возникает вопрос «Почему же природа предпочитает именно эти свойства?» Здесь мы лавируем на грани математического мистицизма [5, с.7]. А может быть ответ прост и лежит на поверхности, как и окончательный ответ на вопрос: «Почему Вселенная устроена так, а не иначе? Действительно, самое непонятное в мире – то, что он понятен. А потому перед тайной рациональности мироздания остаётся лишь благоговейно замереть. Сквозь мир и его духовную структуру просвечивает изначальная творческая мысль, наделённая созидающей силой» (Рацингер)
Если мы говорим о нравственных параллелях между религией и математикой, то этот список был бы неполным без рассмотрения предупреждений, звучащих в Божьих Заповедях, а именно: Не произноси имени Господа, Бога твоего, напрасно. Не убивай. Не кради. Не прелюбодействуй. Не произноси ложного свидетельства на ближнего твоего, и т.д. В математике также имеются свои «заповеди», которые нельзя переступать, например: нельзя делить на ноль, нельзя извлечь корень чётной степени из отрицательного числа, логарифм отрицательного числа не существует, когда речь идет о множестве действительных чисел. «Сухое», академическое преподавание математики ведёт к сужению мотива учебной деятельности, поэтому мы стараемся придать дисциплине привлекательность, используя разнообразную занимательную литературу (в кабинете математики собрано около тысячи различной занимательной и учебно-методической литературы, справочные и занимательные материалы на электронных носителях).
Особый интерес у студентов вызывает изучение темы «Свойства и графики тригонометрических функций». Подготовленная обучающимися презентация (о книге [2] «Математика колебаний, её плюсы и минусы» начинается словами:
u «Многие процессы в окружающем нас мире повторяются: восход солнца, вращения звёзд, разливы рек, биение сердец и т.д. Большинство периодических процессов связаны с колебаниями.
u Колебания всевозможных видов окружают нас на каждом шагу: электромагнитные колебания доносят до нас вести о сложнейших процессах, происходящих внутри звёзд, используются для радио, телевидения, связи с космическими кораблями; акустические колебания нужны для приёма и воспроизведения звука; механические колебания применяют в строительстве, например: для укладки бетона, просеивания сыпучих материалов на виброситах в кулинарии, в медицине – для почти безболезненного высверливания отверстий в зубах и т.д.
u Физическая картина колебательных процессов различна, однако математически их можно охарактеризовать с помощью тригонометрических функций, как дифференциальное уравнение гармонического колебания.»
Эти фразы, предваряющие изучение темы, позволяют понять, что с помощью тригонометрических функций можно описать любые колебательные процессы, в том числе и звуковые колебания. И как не рассказать ученикам о сочетании церковной коллективной молитвы с колокольным звоном по гармонизации пространства, когда от звуковых колебаний колокола погибают вирусы гриппа, расположенные под ним, (доказано экспериментально). Вызывает истинное восхищение и красота волнистой линии (синусоиды), которая является основой многих бордюров, орнаментов, в том числе используется в обрамлении святых икон.
При изучении свойств этих функций рационально использовать примеры удвоения из книги [1]. Пример со стоклеточной шахматной доской ( работник договорился получить плату натурой - зерном таким образом, что на одной клетке – одно зерно, на второй – два, на третьей – четыре, и т.д., когда пришло время расчета, то всего выращенного урожая не хватило. Более того этим зерном можно было обернуть всю землю, слоем в 8 см). Задача об инфузории парамеции, которая каждые 27 часов делится пополам, и если бы все нарождающиеся таким образом инфузории оставались в живых, то сколько бы понадобилось времени, чтобы потомство одной парамеции заняло бы объём, равный объёму солнца. Оказывается всего 130 делений и на 147-е сутки задача будет выполнена. Спасибо естественному отбору. гармонии и равновесию в природе, когда не все парамеции выживают, иначе нам с вами не было бы места на этой земле уже давно. Заслуживает внимания и обратная задача с листком бумаги: листок разрывают пополам, одну из полученных половин снова делят пополам и т.д. Вопрос: сколько таких делений нужно произвести, чтобы получить частицу атомного размера? Студенты называют громадные числа, но в результате несложных подсчётов оказывается, что потребуется всего 80 таких делений.
И самый важный проблемный вопрос: какое из свойств показательной функции продемонстрировали данные примеры? К сожалению, студенты не всегда находят ответ без помощи педагога, а именно: скорость изменения функции (возрастания или её убывания). Естественен и переход к нравственному аспекту скорости изменения, но уже жизненной ситуации, когда преподаватель обращается к студентам с вопросом: «А теперь представьте себе, что вы обидели двоих, и те в свою очередь сделали тоже самое и т.д. Как же быстро может распространиться негатив, обида, злоба (цепная реакция)». Ненависть рождает ещё большую ненависть в ответ, зло рождает ещё большее зло, ведь солнце светит и злым и добрым. Как сказал Господь: «Если вы любите тех, кто любит вас, то какая вам будет за это награда?», «Любите Ваших врагов и молитесь о тех, кто преследует Вас», и ещё одна фраза, полезная для всех: «…будьте совершенны, как совершенен ваш Небесный Отец». После такого общения становятся понятными для всех учеников рекомендации педагога не отвечать на грубость и хамство тем же, не таить в себе обиды, ориентироваться на позитивные эмоции, добрые и полезные дела.
«Геометрия есть познание всего сущего» - писал Платон. Изучая тему Перпендикулярность прямых в пространстве, можно рассмотреть четырёхконечный крест – символ спасения и предмет почитания для христиан. Вертикальный луч (прямая) означает любовь и связь между Богом и человеком, горизонтальная – любовь и связь между людьми. А если мы рассмотрим восьмиконечный крест, символизирующий жертву Христа и вечность (число 8 – знак вечности, знак Воскресения Христа после субботы, седьмого дня), то повернув его на 90, мы получим математический знак бесконечности. Вечность – бесконечность. Пространственные геометрические фигуры и модели мы находим в изобразительном искусстве в православии, в формах церковных зданий (цилиндрические колонны, прямоугольные параллелепипеды зданий, шестиугольные призмы башен и т. д.).
Понятие подобия фигур в геометрии (по образу и подобию), предел функции в алгебре (предел, его не перейдеши), прозрачная сфера в руках ангела ( Зеркало) с сокровенной надписью ИС.ХР.- символ, указывающий, что ангел служит Иисусу Христу и является духом, - да разве можно перечислить все точки соприкосновения религии и математики, способствующие духовному развитию личности студента?! «Математикой нужно заниматься не ради её приложения, а во имя той духовной прибыли, которая связана с ней» - в этих словах Платона заложен глубокий смысл, как и то, что «»Земную науку надо понять, чтобы полюбить, а Божественную надо полюбить, чтобы понять» Б.Паскаль.
Особое внимание хотим обратить на речь педагога, которая должна быть красивой и понятной, образной, выразительной и доброжелательной. В ней не должно быть места для современных сленгов, типа: «Ну ты меня достал» и др. Пословицы, поговорки, устойчивые словосочетания, меткие выражения, афоризмы писателей, учёных, исторических деятелей сделают речь педагога интересной для восприятия её учениками и несомненно обогатят речь самих студентов. С этой целью в помощь православному педагогу составлен словарь образных выражений и крылатых слов (более 200), которые педагог может применить в различных ситуациях на уроке. Вот некоторые из них:
1. А ларчик просто открывался.
Цитата из басни И.А.Крылова «Ларчик» (1808).
Применяется, когда говорят о каком-нибудь деле, вопросе, при разрешении которого
нечего было мудрить.
2. Бумага не краснеет. Бумага всё терпит.
Выражение эти восходят к римскому писателю и оратору Цицерону (106-43 до н.э.); в его письмах «К друзьям» [6,12] находится выражение: «бумага не краснеет», то есть письменно можно высказывать такие мысли, которые стесняются высказывать устно.
3. Буря в стакане воды.
Выражение имеющее значение: «большое волнение но ничтожному поводу» -принадлежит французскому политическому писателю и мыслителю Монтескье (1689-1755).
4. В поте лица.
Выражение употребляется в значении: усердно трудиться, тяжким трудом добывать хлеб. Возникло из библейского мифа. Изгоняя Адама из рая, бог сказал ему: «В поте лица твоего будешь есть хлеб» (Бытие 3,19).
5. Вера горами двигает.
Выражение восходит к евангельскому тексту: «Если вы будете иметь веру с горчичное зерно и скажете горе сей: перейди отсюда туда, и она перейдёт; и ничего не будет не возможного для вас».Утратив религиозную окраску, оно употребляется в значении: убеждённость в правоте какого-либо дела помогает преодолеть все трудности, с ним связанные.
6. Гений-это терпение.
Это выражение приведено в книге французского государственного деятеля Эро де Сешеля (1759-1794).Он посещал француза Бюффона в Монбаре, который по поводу гения сказал эти слова.
7. Да, жалок тот, в ком совесть не чиста.
Цитата из трагедии А.С.Пушкина «Борис Годунов»(1831).Сцена «Царские палаты», слова Бориса.
8. Дом построить на песке.
Выражение возникло из евангельской притчи о «человеке безрассудном», построившем «дом свой на песке».Вскоре, когда пошёл дождь и подул ветер, дом разрушился (Матф.,7,26-27). Выражение это употребляется, когда говорится о чём-нибудь непрочном, необоснованном.
9. Есть от чего в отчаянье прийти.
Цитата из комедии А.С. Грибоедова «Горе от ума» (1824),где Чацкий говорит:
Послушай, ври, да знай же меру;
Есть от чего в отчаянье прийти.
10.Жизнь есть деяние.
Афоризм М.Горького из письма к писателю Л.В.Никулину (1931).
11. Жнёт, где не сеял.
Так говорят о людях любящих пользоваться плодами чужих рук. Выражение возникло из евангелия: «Ты человек жестокий, жнёшь, где не сеял, и собираешь, где не рассыпал» (Матф.,25,24).
12. Зарыть талант в землю.
Выражение возникло из евангельской притчи о том как некий человек, уезжая, поручил рабам охранять своё имение. Употребляется в значении: не заботится о развитии таланта, дать ему заглохнуть.
13. Здоровый дух в здоровом теле.
Выражение это возникло из 10-й сатиры древнеримского поэта Ювенала.
14. И жить торопится, и чувствовать спешит.
Цитата из стихотворения П.А.Вяземского (1792-1878) «Первый снег»(1822).
Поставлена А.С.Пушкиным эпиграфом к 1-й граве «Евгения Онегина».
15. Из дальних странствий возвратясь.
Цитата из басни И.А.Крылова «Лжец»(1812).
16. Кому много дано тому много и взыщется.
Выражение из евангелия (Лука,12,48).
17. Лучше поздно, чем никогда.
Выражение из «Истории народа римского» Тита Ливия (59 до н.э.- 17н.э.).
Нередко цитируется как французская поговорка.
18. Много званных, но мало избранных.
Цитата из евангелия (Матф.,20,16;22,14).
19. Много шуму из ничего.
Заглавие комедии Шекспира (1600), ставшее поговоркой.
20. На сон грядущий.
Выражение, употребляемое в значении «На ночь, перед сном», возникло из молитвенников, в которых имеется раздел молитв «на сон грядущим». Обычно употребляется в измененном виде «на сон грядущий», то есть грядущим назван сон.
21. Не ведают, что творят.
Выражение из евангелия (Лука,23,34). Когда ,согласно легенде, Иисус был распят на кресте, он, обращаясь к богу, сказал: «Отче! Отпусти им, не ведя бо, что творят».
22. Не искушай меня без нужды.
Цитата из стихотворения Е.А.Баратынского «Разуверение» (1821), положенного на музыку М.И.Глинкой (1825).
23. Не мудрствуя лукаво.
Выражение из трагедии А.С.Пушкина «Борис Годунов»(1831).
24. Не о хлебе едином жив будет человек.
Выражение из библии (Второзаконие, 8,3), евангелия (Лука,4,; Матф.,4,4). Употребляется в значении: человек должен заботиться об удовлетворении не только своих материальных, но и духовных потребностей.
25. Не сотвори себе кумира.
Цитата из библии, одна из заповедей Моисея (Исход,20,4). Употребляется в значении: не поклоняйся слепо кому, чему-либо, как идолу.
26. Не судите, да не судимы будете.
Цитата из евангелия (Матф.,7,1-2): «Не судите, да не судимы будете. Ибо каким судом судите, таким будете судимы; и какою мерою мерите, такою и вам будут мерить».
27. От великого до смешного один шаг.
Эту фразу часто повторял Наполеон во время бегства из России в декабре 1812г. своему послу в Варшаве де Прадту.
28. Отойди от зла и сотвори благо.
Выражение возникло из библии: «Уклонися от зла и сотвори благо ,взыщи (ищи) мира и следуй за ним» (Псал.,33,15).
29. Плясать под чужую дудку.
Выражение восходит к греческому историку Геродоту (V в. до н.э.), который рассказывает о попытке персидского царя Кира склонить на свою сторону малоазийских греков, что ему удалось только на определенных условиях.
30. По образу и подобию.
Выражение из библейского мифа о сотворении человека. «И рече бог: сотворим человека по образу нашему и подобию» (Бытие 1,26). Употребляется в значении: чрезвычайно сходно с чем-нибудь.
31. Послушай, ври, но знай же меру.
Цитата из комедии А.С. Грибоедова «Горе от ума» (1824), обращенная к завравшемуся Репетилову.
32. Предел, его же не прейдеши.
Выражение, возникшее из церк.-слав. текста библии (Книга пророка Даниила,6,7-8), употребляется в значении: предел. Рубеж, который нельзя переступить.
33. Рассудку вопреки, наперекор стихиям.
Цитата из комедии «Горе от ума» А.С.Грибоедова
34. С корабля на бал.
Выражение из «Евгения Онегина» А.С.Пушкина (1832).
35. С учёным видом знатока.
Цитата из «Евгения Онегина» А.С.Пушкина.
36. С чувством, с толком, с расстановкой.
Цитата из комедии А.С.Грибоедова «Горе от ума» (1824).
37. Свежо предание, а верится с трудом.
Цитата из коьедии А.С.Грибоедова «Горе от ума».
38. Сейте разумное, доброе, вечное.
Цитата из стихотворения Н.А.Некрасова «Сеятелям» (1877).
39. Только первый шаг труден.
Выражение принадлежит маркизе Дюдеффан (1697-1780), известной своей перепиской с Вольтером.
40. Чтение – вот лучшее учение.
Цитата из письма А.С.Пушкина к брату от 21 июля 1822г.
41. Что и требовалось доказать.
Этой формулой кончается каждое математическое рассуждение великого греческого математика Эвклида (Ш в. до н.э.); употребляется и ныне после доказательства теорем.
42. Что имеем, не храним, потерявши, плачем.
Афоризм из «Плодов раздумий» (1854) Козьмы Пруткова, повторившего название водевиля (1844) С.Соловьёва.
43. Я мыслю, значит существую.
Цитата из сочинения французского философа Рене Декарта (1596-1650) «Начала философии» (1644).
Трудно переоценить важность слов педагога, так как они обладают удивительным свойством зажигать в сердцах воспитанников волшебные чувства верности и благородства, стремления к идеалу, учат великому умению любить жизнь.
