Полный текст статьи
Печать

Сама теория множеств появились не так уж и давно, чуть более ста лет назад. Однако за этот период был пройден большой путь, теория множеств так или иначе фактически стала основой большинства разделов математики.

И начать изучение элементов теории множеств следует с введения основных понятий.

Множество – это фундаментальное понятие, относящее не только к математике, но ко всему окружающему нас миру.

Множество – понятие не определяемое. Определения не существует, но множеством считают совокупность объектов, которые рассматривают, как единое целое. [1]

Чаще всего обозначают большими латинскими буквами: А, В, С и т.п. Элементы – объекты, из которых состоит множество, - записываются в фигурных скобках. Пример:

А = {а, б, в, …, э, ю, я} – множество букв русского алфавита;
N = {1, 2, 3, 4, 5, …} – множество натуральных чисел.

Множество А – конечное, т.е. состоящее из конечного числа элементов, а множество N – бесконечное. Кроме того, следует отдельно выделить, так называемое пустое множество Ø – т.е. не содержащее ни одного элемента. [3]

Принадлежность элемента множеству записывается значком ∈. Соответственно для непринадлежности используют - ∉. Пример:

z ∉ A – буква z не принадлежит множеству целых чисел;
7 ∈ N – число семь принадлежит множеству целых чисел.

Способы задания множеств: во-первых, перечисление всех элементов. Данный способ удобен, нагляден, но используется только для задания конечных множеств.

Пример: A = {а, б, в, …, э, ю, я}

 Во-вторых, множество можно задать с помощью характерного свойства (т.е. свойства, которым обладают все элементы данного множества и не обладают никакие элементы, не принадлежащие ему).

Пример: B = {х | x ∈ Z и x < 100} – множество всех целых чисел, которые меньше 100.

Замечание: иногда одно и то же множество можно задать разными способами и с помощью разных характерных свойств.

Пример: С = {1, 2}
C = {x | x ∈ Z и 1≤x≤2 }
C = {x | x ∈ N и x≤3}

А – подмножество В (или А включается в В) тогда и только тогда, когда все элементы множества А являются элементами множества В. Для обозначения включения используется знак - ⊂. Пример: А ⊂ В – А является подмножеством множества В (или А включается в В). [2]

Любое множество имеет тривиальные подмножества: пустое (Ø ⊂ А) и себя (А ⊂ А).

Два множества равны, если состоят из одних и тех же элементов.

Пример: D = {1, 2}, E = {2, 1} → D = E.

Таким образом, два множества равны тогда и только тогда, когда первое является подмножеством другого, и наоборот.

А = В ↔ (А ⊂ В) и (В ⊂ А)

Данный принцип получил название «принципа объёмности». Метод же доказательства с помощью данного принципа – метод объёмности. [1]

Также следует отметить, что для графического изображения множеств необходимы диаграммы Эйлера-Венна. Используются они во многих областях, не только в теории множеств, но и в теории вероятности, логике, статистике и информатике. При этом множества – это плоские фигуры, а элементы этих множеств – точки.

Для обозначения множества, которое содержит в себе, в качестве подмножеств, все множества данной теории или задачи принято называть универсальным множеством (в рамках данной теории или задачи). Такое множество обозначается знаком U и определяется неоднозначно (т.е. бесконечным количеством способов).

После введения основных понятий следует перейти к основным операциям над множествами. [3]

Пересечение множеств А и В – множество, состоящее из элементов, принадлежащих множеству А и В одновременно.

Обозначают пересечение множеств: A ⋂ В = {x | x ∈ A и x ∈ B} (Рис. 1)  

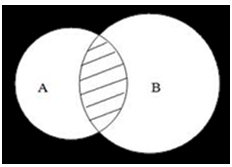
Рисунок 1. Пересечение множеств

Объединение множеств А и В – множество, состоящее из тех элементов, которые принадлежат хотя бы одному из множеств.

Обозначается: А ∪ В = {x | x ∈ A или x ∈ B} (Рис. 2)

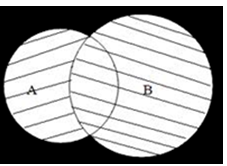Рисунок 2. Объединение множеств

Симметрическая разность А и В – множество, состоящее из тех элементов, которые принадлежат А и не принадлежат В или наоборот.

Обозначается: А Δ В = {x | (x ∈ A и x ∉ B) или (х ∉ А и х ∈ В)} (Рис. 3)

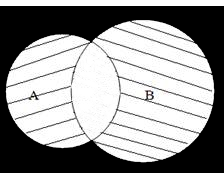Рисунок 3. Симметрическая разность множеств

Теперь обратимся к практическому применению теории множеств в условиях компьютерного моделирования. Для наглядности рассмотрим задачи на 3D-моделирование в такой программе как 3ds  Max.

Задача «Кусок сыра».

Чтобы получить дырки для куска сыра, необходимо к начальному множеству А (цилиндр) и множеству В (шар) применить операцию разность. Далее для получения полноценного куска сыра используем операцию пересечения множеств А и С (куб). (Рис. 4).

Рисунок 4. Кусок сыра

Задача «Планета».

Для получения кольца (множество С) необходимо к множеству А (шар) и множеству В (цилиндр) применить операцию разность. (Рис. 5).

Рисунок 5. Получение кольца

Затем объединяем множества С (кольцо) и А (шар). Получаем планету.
(Рис. 6).


Рисунок 6. Планета

Задача «Кусок пиццы».

Используем два начальных множества А (цилиндр) и В (куб). При пересечении части множества А  и множества В получаем кусок пиццы. (Рис. 7).


Рисунок 7. Кусок пиццы

Таким образом, на практическом примере решения подобных задач мы убедились, что теория множеств имеет важное прикладное значение и может применяться в компьютерном моделировании, например при создании реальных объектов.