Анализ возможностей использования информационных технологий при проведении эконометрических исследований

Главной задачей эконометрики является количественная оценка имеющихся взаимосвязей между экономическими явлениями и процессами в целях построения эконометрических моделей и определение возможности их практического использования для анализа и прогнозирования. Специалисты с помощью наблюдений стремятся выявить скрытые зависимости и выразить их в виде формул, т. е. математически смоделировать явления или процессы. Такую возможность предоставляет регрессионный анализ – один из видов предсказательного моделирования, с помощью которого оцениваются коэффициенты искомого уравнения. Как известно, базовым методом регрессионного анализа является метод наименьших квадратов (МНК), основанный на минимизации суммы квадратов остатков регрессии. В случае многофакторных линейных экономических зависимостей применение МНК приводит к решению систем линейных алгебраических уравнений большой размерности, при этом существенная доля времени разработчика тратится на создание правильных инструментов анализа, способов визуализации обрабатываемой информации и документирование результатов, то есть на рутинную работу, отвлекающую от непосредственной исследовательской деятельности. В связи с этим возникает необходимость в широком применении компьютерных средств обработки информации. Анализ эконометрических программ показал, что в настоящее время наиболее часто используются следующие зарубежные программные продукты:

-            программы, ориентированные на программирование (R-проект и другие);

-            статистические программы общего назначения, которые содержат широкий набор статистических функций и процедур (Statistica, SPSS);

-            программы, ориентированные на решение широкого круга эконометрических задач (EViews, Stata, Gretl);

-            электронные таблицы (Excel) [3].

Эконометрические программы различаются своей функциональностью, способом представления данных и организацией диалога с пользователем.

Целью данной статьи является сравнительный анализ возможностей проведения регрессионного анализа средствами пакетов прикладных программ.

Табличный процессор MS Excel предоставляет средства для построения классических линейных регрессионных моделей, при этом возможны два подхода:

-            способ «ручной» обработки, при котором используется исходный массив экспериментальных данных (данных наблюдений) в виде многомерной таблицы значений результативных и факторных признаков. На основе исходного массива проводится расчет коэффициентов уравнения регрессии и оценка качества полученного уравнения по определенным критериям. Данная процедура требует построения довольно обширной таблицы вспомогательных значений, больших временных затрат, напряжения и внимания экспериментатора. При этом часто приходится корректировать выполненные расчеты и устранять допущенные ошибки;

-            использование (для упрощения расчетов) различных встроенных функций и функций из надстройки «Пакет анализа» [1].

Таким образом, пакет прикладных программ Excel в основном позволяет проводить только линейный регрессионный анализ, при этом реализация сложных эконометрических процедур требует от пользователя безупречного знания всех вычислительных алгоритмов, значительного расчетного времени и трудоемкости вычислений. Поэтому использование Excel даже при изучении базового курса эконометрики является недостаточно неэффективным.

Подробный сравнительный анализ возможностей эконометрического программного обеспечения [2] говорит о том, что наиболее полный перечень методов эконометрики для анализа временных рядов, пространственных и панельных данных, а также методов многомерного статистического анализа содержат программы Gretl и Stata. Пакет Eviews уступает им лишь из-за невключения методов многомерного анализа. Если учесть комбинацию критериев «возможности + цена», то безусловным лидером остается программа Gretl.

Реальные процессы в экономике сложны и характеризуются, как правило, нелинейными многофакторными зависимостями. Проведение многофакторного линейного  и нелинейного (с предварительной линеаризацией аналитической зависимости) регрессионного анализа сводится, в конечном счете, к решению систем линейных алгебраических уравнений большой размерности, что, в принципе, не свойственно пакету MS Excel [3]. Вполне разумно предположить, что в данном случае целесообразнее всего применять инструменты, изначально созданные для работы с матрицами. Таким инструментом является система MatLab.

Система MatLab представляет собой хорошо апробированную и надежную систему компьютерной математики (СКМ), рассчитанную на решение самого широкого круга математических задач с представлением данных в универсальной (но не навязываемой пользователям) матричной форме, предложенную фирмой Math Works, Inc. Для решения задач регрессионного анализа данная система предоставляет множество математических функций для работы с векторами и матрицами, а непосредственно для решения задач корреляционно-регрессионный анализа – панель инструментов Statistics Toolbox [4]. В состав панели Statistics Toolbox включены более 25 функций линейного регрессионного анализа и более 5-ти функций нелинейного регрессионного анализа. MatLab обладает также богатейшей коллекцией функций для обычной и специальной графики, которую можно использовать при проведении графического анализа [5]. Что наиболее ценно, система MatLab постоянно развивается, в каждой её новой версии появляются все новые и новые модули и функции. К сожалению, в наших странах MatLab недостаточно полно привлекается для решения эконометрических задач, отечественных разработок и специальной литературы по этому направлению недостаточно, в основном используются зарубежные источники.

Основными функциями для проведения линейного регрессионного анализа в системе MatLab являются функции polyfit, polyval, regress и regstats.

Функция polyfit возвращает полином в виде вектора его коэффициентов, при этом решается следующая задача: для набора данных  требуется найти такой полином степени n , коэффициенты которого являются решением задачи минимизации . Чтобы такой полином был единственным, его степень должна быть меньше количества заданных точек.

Функция polyval вычисляет прогноз с использованием полиномиальной регрессии, получаемой с помощью функции polyfit.

Функция regress используется для нахождения множественной линейной регрессии.

Функция regstats используется для диагностирования линейной множественной модели с использованием графического интерфейса, при этом функция отображает графическое окно с набором статистик, служащих для оценки качества множественной регрессионной модели. Для выбора статистик необходимо отметить соответствующие флажки.

В одной из последних версий MatLab 2012b для проведения регрессионного анализа появились новые функции LinearModel, NonLinearModel и GeneralizedLinearModel. Функция LinearModel предназначена для расчета линейных моделей, NonLinearModel используется для нелинейной регрессии, а GeneralizedLinearModel используется для логистической регрессии и других видов обобщенных линейных моделей [4, 6].

Возможности использования системы MatLab в эконометрических исследованиях автором статьи оценивались результатами проведения регрессионного анализа с помощью приложений MS Excel и MatLab при моделировании явно нелинейной функции одного аргумента вида: y(х)=1/x+0,01x²+ε, где ε – остаточная случайная величина, задаваемая в системе MatLab последовательностью псевдослучайных нормальных чисел с математическим ожиданием, равным нулю, и среднеквадратическим отклонением, равным единице, генерируемых с помощью уравнений:

Качество полученных уравнений регрессии оценивалось величиной коэффициента детерминации .

Как показали результаты исследования, оценки коэффициентов уравнения, полученные средствами Excel (Регрессия) и MATLAB (polyfit), практически не отличаются друг от друга (R² соответственно равен 0,843 и 0,844). Это говорит, видимо, о том, что алгоритмы расчета регрессий в обоих приложениях одинаковы. Однако число операций, выполняемых в MatLab значительно меньше – всего лишь одно обращение к функции polyfit без предварительной линеаризации исходного уравнения и составления вспомогательной расчетной таблицы. Кроме того, в MatLab имеется возможность аппроксимации экспериментальных данных полиномом практически любой степени, вплоть до 10-й. Таким образом, в системе MatLab имеется возможность на стадии спецификации модели прямо на поле корреляций с помощью графических средств определить вид необходимой аналитической зависимости, связывающей включенные в модель переменные, путем подбора на панели Basic Fitting степени наиболее оптимального аппроксимирующего полинома и получения его уравнения (Рисунок 1).  

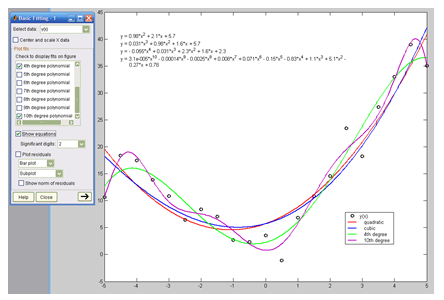
Рисунок 1 – Графический регрессионный анализ 

Результат такого графического анализа можно использовать в последующем расчете регрессии с помощью функции polyfit, вводя в неё выбранную степень полинома.

На основе проведенных исследований можно прийти к выводу, что при обучении эконометрическим дисциплинам наряду с использованием известных пакетов эконометрических программ целесообразно также использовать систему MatLab, которая может значительно упростить процесс проведения регрессионного анализа и расширить кругозор обучаемых.