Полный текст статьи
Крутихина Марина Викторовна,
кандидат педагогических наук, доцент кафедры математического анализа и методики обучения математике ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров
Чулкова Виктория Михайловна,
студентка факультета информатики, математики и физики ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров
Аннотация. Статья посвящена анализу использования задач с практическим содержанием на ГИА по математике как средству обучения элементам математического моделирования.
Ключевые слова: задачи с практическим содержанием, математическое моделирование, ГИА по математике.
Математика на протяжении всей истории человеческой культуры всегда была ее неотъемлемой частью; она является ключом к познанию окружающего мира, базой научно-технического прогресса и важной компонентой развития личности. Математические знания и навыки необходимы практически во всех профессиях, прежде всего в тех, которых связаны с естественными науками, техникой, экономикой. Важность освоения таких математических компетенций, как умение применять задания в практической жизни и в смежных областях подчеркнуто выделением в последние годы в государственной итоговой аттестации. отдельного модуля «Реальная математика».
Государственная итоговая аттестация (ГИА) в 9-ом классе и ЕГЭ в 11-ом классе не только осуществляют контроль качества обучения школьников, полученных ими знаний, выработанных умений и навыков, сформированных компетенций. Структура и содержание этого экзаменов задают ориентиры всего математического образования, влияют на отбор содержания, выбор форм и методов обучения. Поэтому так важно, чтобы содержание ГИА по математике соответствовало целям и задачам математического образования школьников, способствовало повышению его качества.
Сейчас общепризнанно, что роль практических задач в ГИА по математике должна быть усилена. Это обусловлено той ролью, которую практическая математика играет в современной жизни, а также в образовании, воспитании и развитии подрастающего поколения.
Выше говорилось, что задачи с практическим содержанием представлены в ГИА в модуле «Реальная математика». Модуль содержит семь задач (из двадцати шести заданий): задание 14 – с выбором правильного ответа из предложенных вариантов, 15–20 – задания с кратким ответом в виде целого числа, конечной десятичной дроби или последовательности цифр. Все задачи представлены в первой части.
Задачи «Реальной математики» охватывают такие разделы школьного курса математики, как числа и вычисления, алгебраические выражения, функции и графики, геометрию, статистику и теорию вероятностей.
В этой части экзаменационной работы содержатся задания, отнесенные к категории «Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели». Это задания, формулировка которых содержит практический контекст, знакомый учащимся или близкий их жизненному опыту. Из них одно задание проверяет умение применять геометрические знания, а остальные задания предназначены для проверки знаний из разделов: арифметика, алгебра, теория вероятностей и статистика.
Выделяют следующие умения, которые проверяются при решении практических задач в ГИА.
– Решать несложные практические расчетные задачи; решать задачи, связанные с отношением, пропорциональностью величин, дробями, процентами; пользоваться оценкой и прикидкой при практических расчетах; интерпретировать результаты решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых объектов.
– Пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот. Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами.
– Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимостей.
– Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин.
– Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках.
– Решать практические задачи, требующие систематического перебора вариантов; сравнивать шансы наступления случайных событий, оценивать вероятности случайного события, сопоставлять и исследовать модели реальной ситуацией с использованием аппарата вероятности и статистики.
Анализ результатов выполнения заданий по алгебре показывает, что учащиеся лучше справляются с заданиями алгоритмического характера, нежели с заданиями на понимание, практическое применение или решение задач. Например, с задачами на проценты по-прежнему справляется около 75% учащихся. Остальные ученики допускают типичную ошибку при решении задач на уменьшение или увеличение величины на несколько процентов.
Мы считаем, что многих ошибок можно избежать, если рассматривать решение задач с практическим содержанием с точки зрения обучения математическому моделированию. В школьных учебниках по математике последнего поколения понятие математической модели встречается уже в 5-ом классе. В систематическом курсе алгебры рассматриваются этапы моделирования, основные свойства модели. Однако, как показывает практика, учителя не обращают должного внимания на этот материал, так как он до последнего времени не являлся предметом итогового контроля.
Некоторые вопросы методики изучения элементов математического моделирования изложены нами в [1]. Мы считаем, что наиболее целесообразно и возможно в основной школе формировать следующие умения: замена исходных терминов выбранными математическими эквивалентами; оценка полноты исходной информации и введение при необходимости недостающих числовых данных; выбор точности числовых значений, соответствующих смыслу задачи; выявление возможности получения данных для решения задачи на практике. Приведем примеры задач из тестовых материалов ГИА, при решении которых необходимы названные умения.
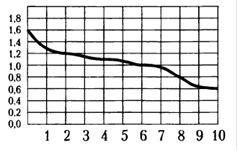
Задача 1. При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси – напряжение в вольтах. Определите по рисунку, каким было напряжение в момент включения фонарика. Ответ дайте в вольтах.
Задача 2. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-хклассов.
| Мальчики | Девочки | |||||
| Отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Время, секунды | 4,6 | 4,9 | 5,3 | 5,0 | 5,5 | 5,9 |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.
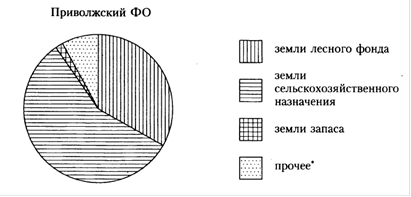
Задача 3. На диаграмме показано распределение земель Приволжского Федерального округа по категориям. Определите по диаграмме, в каких пределах находится доля земель лесного фонда.
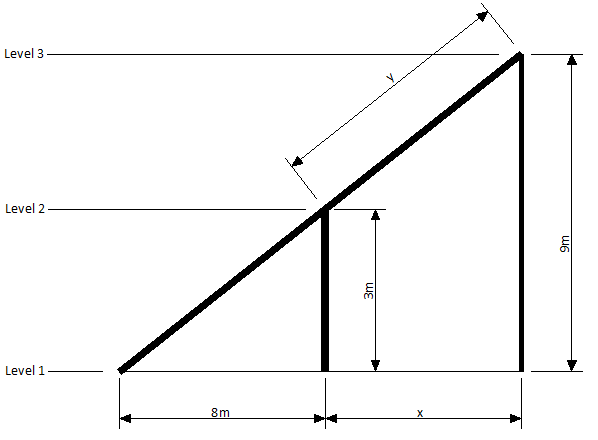
Задача 4. На фабрике используется наклонная конвейерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвейер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1. Фабрика хочет модернизировать конвейер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвейера.
Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвейера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.
Таким образом, анализ контрольно-измерительных материалов ГИА показывает, что для успешной сдачи экзамена учащимся необходимо владеть простейшими элементами математического моделирования, названными выше. Результаты аттестации говорят о том, что даже с простейшими задачами справляются не все учащиеся. Основная причина этого явления - отсутствие должного внимания к вопросам моделирования учителей и задач в школьных учебниках.
Ссылки на источники
1. Крутихина М. В. Обучение некоторым элементам математического моделирования как средство подготовки к профильному образованию // Математический вестник педвузов и университетов Волго-Вятского региона. Выпуск 6. – Киров, 2004. – С. 246–254.

 М.
В. Крутихина
М.
В. Крутихина