Полный текст статьи
Печать

Аннотация. Статья посвящена вопросам развития исследовательских умений учащихся в процессе решения математических задач с параметрами.
Ключевый слова: задачи с параметрами, учебно-исследовательская деятельность, исследовательские умения

В  материалах ЕГЭ регулярно содержатся задачи с параметром,  которые часто присутствовали на вступительных экзаменах в вуз с высокими требованиями к математической подготовке абитуриентов. Контрольно-измерительные материалы для единого государственного экзамена создаются на основе кодификаторов элементов содержания и требований к уровню подготовки выпускников. Решение данных задач с одной стороны, относятся к элементам содержания «Уметь решать уравнения и неравенства», а с другой стороны, требуют определенного уровня сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезы, оценивать результаты. Таким образом, решение задач с параметром можно считать деятельностью, близкой по своему характеру к исследовательской, а формирование указанной компетенции является одним из важных метапредметных результатов, реализуемого в рамках внедрения и апробации ФГОС среднего (полного) образования. В связи с этим, с одной стороны,  решение задач с параметрами важно использовать для развития математического мышления.

С другой стороны, школьники относят задачи с параметрами к самому сложному материалу, объясняя это несколькими причинами: трудность в выборе способа решения, отслеживания возникающих «ветвлений», исследования всех вариантов решений.  Результаты выполнения выпускниками в 2012 и 2014 году задания С5 показали, что более 80% выпускников даже не приступали к выполнению задания[1]. В таблице 1 представлено процентное  соотношение выпускников, набравших соответствующее количество баллов.

Таблица 1.

Общие результаты выполнения задания С5. 

Балл

2014г.

2012г.

1

1,4%

3,7%

2

0,2%

0,8%

3

0,1%

0,6%

4

0,2%

1,1%

 Кроме того, зачастую, учителя даже не рассматривают такие задачи с учениками, считая их заданиями повышенного уровня сложности, с  которыми слабые ученики априори не смогут справиться.

Аналогичное положение задач с параметрами в учебно-методических комплектах по математике, утвержденных или рекомендованных к использованию в общеобразовательной школе Министерством образования и науки РФ: их количество в любом из общефедеральных комплектов не превосходит 1%.  

Мирошин В.В. [2] выделяет отдельную часть математики – «абитуриентскую», которая существует отдельно от школьной программы. Действительно,  задачам с параметрами посвящены множество сборников для поступающих в вузы, в которых рассмотрены разнообразные приемы и методы решения. Однако педагоги сталкиваются с серьезными методическими проблемами при обучении решению таких задач, по причине того, что в большинстве этих пособий  не учат, как выбрать тот или иной способ решения, как научиться решать эти задачи.

Если же рассматривать решение задач с параметрами  не как  самоцель, а как средство развития активной творческой деятельности учащегося, его системного мышления, то целесообразно организовать учебно-исследовательскую  деятельность, в ходе которой ученик развивает умения самостоятельно приобретать и применять знания, формулировать и аргументировать позицию. Учащиеся, владеющие методами решения задач с параметрами, успешнее справляются (и опыт это подтверждает) [2] с другими задачами, поэтому в школьной математике таким задачам должно уделяться большое внимание.  

Известный  петербургский педагог В.И. Рыжик отмечает, что многолетняя ориентация на ЗУНы привела к тому, что основное внимание в школе уделяется учебной деятельности, в рамках которой, основным занятием стало усвоение алгоритмов и алгоритмических предписаний[3]. Уравнения (неравенства) с параметрами относятся к иному типу задач – задач, для решения которых необходимо прежде всего, умение проводить довольно разветвленные – логические построения и исследования. В теории обучения математике разработаны методические основы исследовательских задач, которые позволяют сравнить структуру типовой и исследовательской задачи [4,5]. На рис. 1 показано, что рассматриваемые в статье задачи обладают всеми признаками исследовательской задачи.

 

Проанализировав и обобщив ряд исследований[4,5,6,7,8], необходимо выделить общие положения в определениях учебно-исследовательской деятельности:  вид познавательной деятельности, цель которой не научные открытия учащихся, а развитие у них соответствующих личностных качеств, умений исследования как универсального способа освоения действительности. При этом учебно-исследовательская деятельность имеет определенные структурные компоненты, характерные для научного исследования: выделение (уточнение проблемы), организация и анализ данных, выдвижение и проверка гипотезы, формулировка выводов. Рассмотрим основные этапы учебного исследования на простой задаче о линейных функциях. 

Таблица 2.

Основные этапы учебного исследования

№ п/п

Основные этапы учебного исследования на примере задачи с параметром линейной функции

  1.  

Цель. Мотивирующей (исходной) задачей, которая должна обеспечить «видение» учащимися более общей проблемы, может служить следующая задача: существует ли три числа a,b,c, что f1(x)= ax+b, f2(x)= bx+c, f3(x)= cx+a 
  1.  

Проблема и направления исследования – самый сложный и «творческий» компонент учебного исследования. Хорошо, если ученик сам может сформулировать проблему, но в реальной школьной практике самостоятельное определение проблемы затруднено.

Проблема: в определении существования параметров a,b,c  для построенного чертежа.
Направления исследования:
1)определить положения прямых, в зависимости от параметров;
2) установить точки пересечения прямых с осями координат.
  1.  

Выдвижение гипотез. В гипотезе формулируется утверждение о результате, который предположительно должен получиться. Не нужно ограничивать число предлагаемых учащимися гипотез.
В данной задаче гипотеза:  «такие числа существуют».
  1.  

Обоснование гипотез, получивших ранее подтверждение или ложность при помощи контрпримеров, используя  выделенные направления исследования на этапе 2.
1)    точки пересечения прямых f1(x)= ax+b, f2(x)= bx+c, f3(x)= cx+a с осью ординат будут соответственно b,c,a, тогда b>c>a;
2)    рассмотрим, от чего зависит наклон прямых: учитель организует практическую работу  по построению прямых с различными угловыми коэффициентами, в результате чего будет сделан вывод о зависимости значения угловой коэффициента от его положения на координатной плоскости. Тогда, снова обратившись к рис.2, учащиеся увидят что прямая f1(x)= ax+b – имеет самый крутой угол наклона, значит a<b<c.
В результате гипотеза оказалась ложной.
 

Презентация результатов является заключительным этапом выполнения исследовательского задания.

Рассмотренная задача с параметрами не является сложной, однако  иллюстрирует  важные свойства линейной функции, обладает высокой диагностической и прогностической ценностью. В процессе ее решения развиваются умения составлять соотношения, выдвижение различных предположений с обоснованием их возможности (гипотезы), формулирование обобщенного теоретического принципа, объясняющего сущность задачи.

Ниже приведем еще пример задачи с параметрами с описанием исследовательских умений, которые формулируются при их решении.

Задача: При каких значениях параметра а система уравнений

x+y=a

x2+y2=9  имеет единственное решение?

Задача может решаться несколькими способами.

Один из способов, так называемый аналитический,  получается, если из первого уравнения выразить y через х, подставить найденное выражение во второе уравнение, получив при этом квадратное, относительно х, далее проанализировать дискриминант уравнения.

Другой способ решения получается при рассмотрении геометрической интерпретации задачи: первое уравнение описывает прямую, расположенную под углом 450 к оси Ох, а второе окружность с центром в начале координат и радиусом 3. При расположении прямой и окружности возможны три варианта:

1)    Прямая  пересекает окружность в двух точках;
2)    прямая касается окружности;
3)    прямая проходит вне окружности.

Легко увидеть, что единственное решение система будет иметь только при касании прямой СЕ и окружности с центром в начале координат и радиусом 3. При этом значение а можно определить как катет ОС равнобедренного прямоугольного треугольника ОСВ, в котором известна высота.

 1
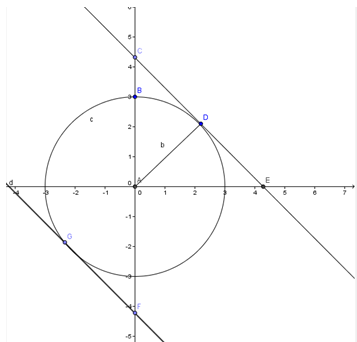
Рис.3 Графическая интерпретация задачи 

В процессе решения этой задачи у учащихся формируется умение  решать задачу несколькими способами, уметь конструировать новый способ на основе ранее изученных, уметь применять вспомогательный прием, умение решать задачу с необычным содержанием обычным способом, уметь проводить прямой и обратный ход рассуждений.

Ссылки на источники

  1. И.В.Ященко, А.В.Семенов, И.Р.Высоцкий Методические рекомендации по некоторым аспектам совершенствования преподавания математики. – М.:ФИПИ, 2014.-34с.
  2. Мирошин В.В. Решение задач с параметрами. Теория и практика/В.В.Мирошин.- М.:Издательство «Экзамен», 2009.-286с.
  3. В.И.Рыжик Кризис среднего математического образования глазами учителя// Математика в школе, 2014,№1-с.3-9.
  4. Колягин, Ю. М. Задачи в обучении математике. Ч.1. Математические задачи как средство обучения и развития учащихся [Текст] / Ю. М. Колягин. – М.: Просвещение, 1977. – 108с.
  5. Крупич, В. И. Теоретические основы обучения решению школьных математических задач [Текст] / В. И. Крупич. – М.: Прометей, 1995. – 166с.
  6. Далингер В.А. Поисково-исследовательская деятельность учащихся по математике: Учебное пособие. – Омск: Изд-во ОмГПУ, 2005. – 456 с.
  7. Савенков А.И. Психологические основы исследовательского обучения щкольников// Физика : проблемы преподавания.-2007.-№7.-с.14-24
  8. Алексеев Н. Г., Леонтович  А. В., Обухов  А. В., Фомина  Л. Ф. Концепция развития исследовательской деятельности учащихся // Исследовательская работа школьников. 2001. №. 1. С. 24-34.