Опыт применения электронных образовательных ресурсов на уроках математики

Аннотация. В статье представлен опыт работы учителей математики МОАУ «Лицей №21» города Кирова в использовании электронных образовательных ресурсов для подготовки к проведению уроков, непосредственно в ходе них, а также для учащихся, проявляющих затруднения при изучении предмета или пропустивших уроки.
Ключевые слова: электронные образовательные ресурсы, обучение математике, математический конструктор, geogebra, наглядная математика 

Одной из задач, отмеченных в концепции развития математического образования, является обеспечение наличия общедоступных информационных ресурсов, необходимых для реализации учебных программ математического образования, в том числе в электронном формате, инструментов деятельности обучающихся и педагогов, применение современных технологий образовательного процесса. Таким образом, в практику преподавания нашей дисциплины приходят все быстрее и интенсивнее развивающиеся электронные образовательные ресурсы.

В современных условиях при всеобщей интернетизации электронные образовательные ресурсы (ЭОР) можно условно разделить на две группы: требующие подключения к сети Интернет (различные образовательные сайты, сетевые программы и т.п.) и работающие от него независимо (презентации, интерактивные учебные пособия и т.п.). Не останавливаясь подробнее на классификации, опишем, каким образом мы в МОАУ «Лицей №21» города Кирова используем возможности некоторых образовательных сайтов и обучающих программ для подготовки к проведению уроков, непосредственно в ходе них, а также для учащихся, проявляющих затруднения при изучении нашего предмета или пропустивших урок.

Проект федерального центра информационно-образовательных ресурсов (ФЦИОР) fcior.edu.ru направлен на распространение электронных образовательных ресурсов и сервисов для всех уровней и ступеней образования. 

Данный сайт содержит несколько тысяч разработок трех типов модулей: информационные (для изучения новой темы или ее повторения), практический (направлен на отработку решения задач) и контрольный (для проведения оценочной деятельности). Для открытия файлов, скачанных с этого сайта, необходимо установить дополнительное программное обеспечение, которое есть там же в открытом доступе.

Рассмотрим на примере модуля «Кубическая функция» возможности использования материалов ФЦИОР. Данный модуль интересен своей исследовательской основой, поскольку позволяет рассмотреть расположение и форму графика кубической функции на координатной плоскости в зависимости от значений коэффициентов, входящих в запись ее уравнения. Двигая ползунки, которые меняют значения коэффициентов, можно наблюдать, как при этом меняется график. Также приведена система заданий, которая позволяет, проанализировав расположение и форму графика, связать это с коэффициентами. Хоть данный модуль и относится авторами к разделу «Применение производной к исследованию функций», но он может быть также полезен при решении задач с параметрами, построении графика кубической параболы и т.д.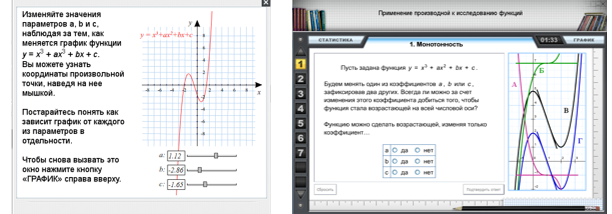

Сайт единой коллекции цифровых образовательных ресурсов http://school-collection.edu.ru/ содержит цифровые наборы (в основном в форме презентаций) к различным школьным учебникам, поурочные планирования, методические рекомендации. 

Особое внимание хотелось бы уделить программе, доступной к скачиванию на данном сайте – «Математический конструктор». Данная программа проста в использовании, обладает широким спектром функций, достаточным для выполнения множества заданий и решения самых различных вопросов. Например, на скриншоте ниже представлено графическое решение уравнения с автоматическим поиском координат точек пересечения.

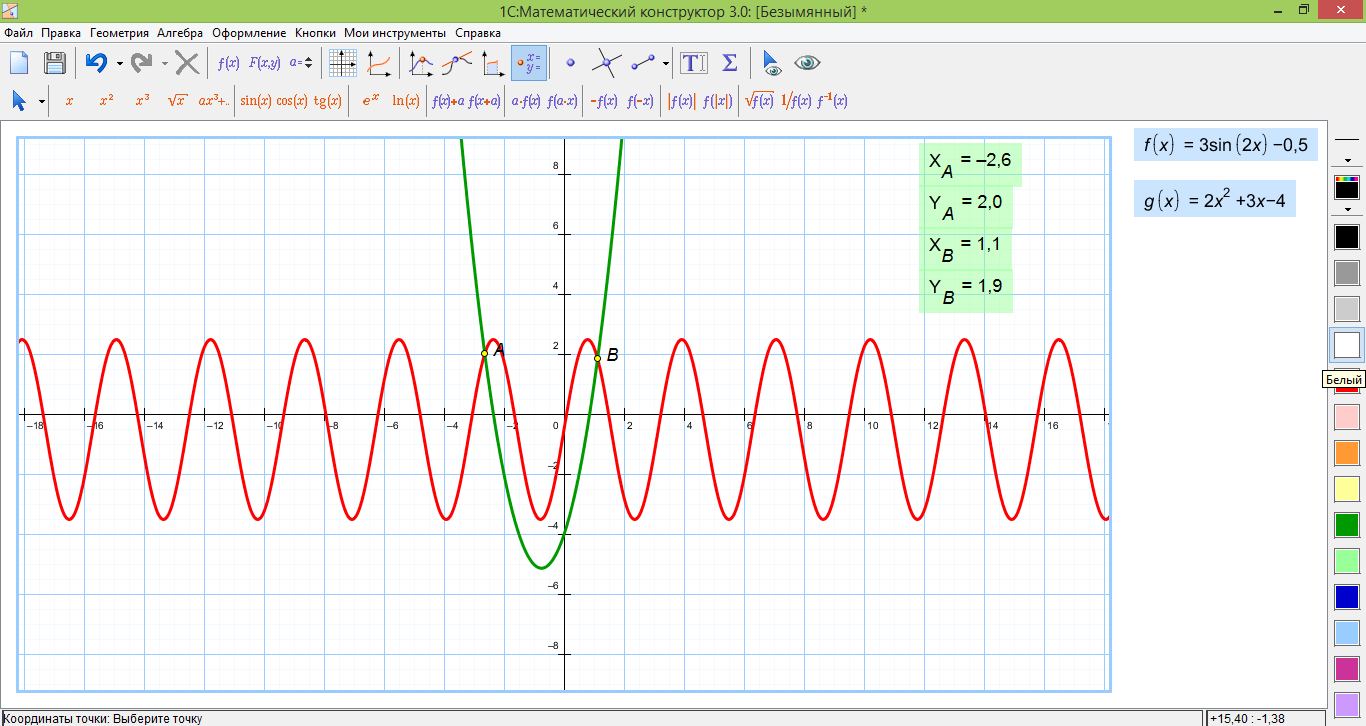
Есть возможность построения графиков самых различных функций, автоматически производить их преобразования (сдвиги, растяжения, отражения относительно осей), находить экстремумы, строить касательные, закрашивать области под графиками, выполнять действия над областями (пересечение, объединение и т.п.). В данной программе можно строить самые различные геометрические объекты (в основном планиметрические), осуществлять ряд преобразований с ними (например, деление угла на несколько частей, проведение через произвольную точку перпендикуляра к прямой). Все это может быть полезно прямо на уроке, когда необходимо быстро и качественно сделать чертеж к задаче, выполнить проверку найденного решения. Конечно, набор функций не исчерпывается перечисленными и заслуживает отдельного детального рассмотрения.

Еще один интересный ресурс http://www.geogebra.org/. Особая ценность данного ресурса составляет то, что с ним можно работать в любых операционных системах и на любых устройствах, включая мобильные телефоны и планшеты. С ней можно работать как через Интернет, так и скачав приложение на компьютер. Геогебра позволяет как скачивать готовые материалы, так и на своей платформе создавать свои. Огромная коллекция накопленных приложений имеет лишь один существенный недостаток – многие из них на иностранных языках. Есть возможность поиска по хэштегам (ключевым словам, которым предшествует символ #). 

Приведем несколько примеров: приложение, которое демонстрирует тригонометрическую окружность с возможностью рассмотреть синусы и косинусу углов, измеряемых как в градусах, так и в радианах (http://tube.geogebra.org/student/m62198), доказательство теоремы косинусов через теорему об отрезках пересекающихся хорд, где можно менять вид треугольника, а в соответствии с ним меняется и вся демонстрация доказательства (http://tube.geogebra.org/student/m18967), задача с параметром и модулем «Найдите все значения параметра  , при каждом из которых неравенство  не имеет решений на отрезке  » (http://tube.geogebra.org/student/m46838).

Используемых нами образовательных сайтов очень много. Сайт http://www.openclass.ru содержит авторские разработки учителей. На сайте http://www.interneturok.ru собраны видеоуроки по различным предметам, в том числе и по математике (они могут быть полезны детям, которые пропустили темы), конспекты, тренажеры и проверочный тест к каждому уроку. Сайт http://www.smartboard.ru содержит материалы для работы с интерактивной доской.

Последние два года к активной работе мы подключаем сайт нашего методического объединения http://математики-лицея21.рф, который помимо текущих новостей, содержит информацию о работе нашей инновационной площадки и публикации наших учителей. В ходе недели математики мы провели конкурс «Великие математики». За день на сайте были опубликованы 30 неподписанных портретов известных математиков. На следующий день представители от класса подходили к ответственному лицу и наудачу вытягивали номер портрета, который им нужно идентифицировать. Дополнительные баллы начислялись тем классам, которые нашли всех ученых. 
Помимо этого, нами используются программные средства интерактивного учебного пособия «Наглядная математика».

В нашей коллекции диски по следующим темам «Тригонометрические функции, уравнения и неравенства», «Треугольники», «Многоугольники», «Стереометрия», «Векторы», «Графики функции», «Многогранники. Тела вращения». К каждому диску приложены руководство пользователя и методические рекомендации по их использованию. Особую полезность для нас представляет диск «Стереометрия», поскольку содержит не только необходимый теоретический материал, но и 3D-рисунки различных стереометрических объектов, которые можно двигать, крутить и перемещать, а также систему тестовых вопросов и задач к каждой теме.

Другой пример простой независимой от Интернета программы – Арифметические действия с обыкновенными дробями, разработанная С.А. Ермолиным. Она позволяет отработать навык действий с дробями. Данную программу можно использовать как в начале изучения действий с дробями, так и в ее конце при проверке устного счета для учащихся разного уровня, поскольку есть возможность выбрать сложность (чем больше номер урока, тем сложнее задания для их устного решения). Также она будет ценна и для родителей, поскольку они могут самостоятельно проконтролировать своих детей дома – программа выдаст оценку и отметит ошибки, подскажет о недочетах (например, о том, что учащийся забывает сократить получившуюся в результате дробь или неправильно выделяет целую часть). Можно проводить индивидуальную диагностику с помощью данной программы, она сведет результаты в единую таблицу с полным отчетом по каждому учащемуся.

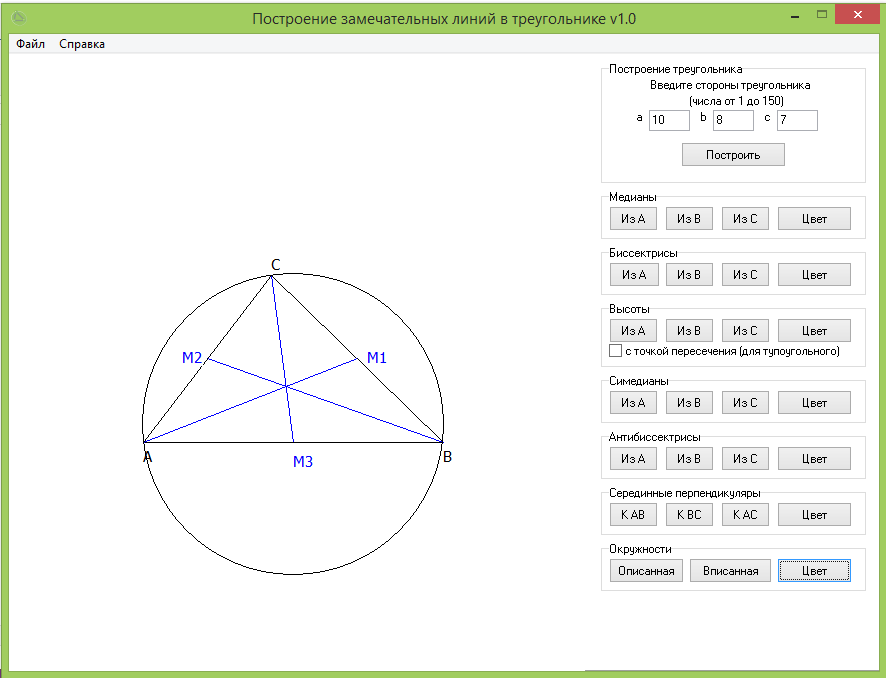
Другой пример – программа Построитель, которая может быть использована как для подготовки урока (поскольку изображения можно сохранять и вставлять, например, в презентации), так и для демонстрации учащимся некоторых фактов о замечательных линиях в треугольнике. При использовании на уроках обязательно возникнут вопросы «А что такое симедиана и антибиссектриса?», которые можно предложить, например, как тему семинара на одном из дополнительных занятий.

Но работать необходимо не только с монитором компьютера или интерактивной доской. Бумажные носители информации не должны терять своей образовательной полезности. С другой стороны, они должны трансформироваться в новые формы и представления, интересные современному ребенку. Одной из таких форм мы считаем стилизованный ученический дневник. 

Каждому лицеисту, учащемуся в математическом классе или с перспективой на него, был выдан дневник, содержащий не только всю необходимую информацию об организации учебного труда (информация об ученике, о Лицее, об учителях, расписании и т.д.), но и справочник с математическими формулами. Также на каждой неделе в верхней части страницы слева содержится высказывание о математике известных людей, а справа интересный факт об этом человеке. Таким образом, нами отмечена важность науки порой для самых отдаленных от нее людей и ее вдохновляющая основа для ученых самых разных областей.

Итак, современное техническое оснащение как кабинета математики, так и рабочего места школьника у него дома позволяет значительно расширить его информационное пространство. Наша задача дать правильный вектор этого расширения, показать учащемуся, что математика не ограничивается решением задач из учебника, а может быть представлена самыми различными образовательными формами, при использовании которых процесс обучения для ребенка вполне может стать просто незаметным