Аннотация. В статье описывается форма внеурочной деятельности как способ повышения интереса к математике. Обосновано показана необходимость включать математические игры в образовательный процесс; предлагается разработка игры-путешествия в Древний Рим.
Ключевые слова: внеурочная деятельность, математическая игра, развитие интереса к математике, решение задач.
Современная система образования переживает сейчас не лучшие времена. Концепции и программы в образовательных учреждениях подвергались неоднократным пересмотрам. Но главная цель школьного обучения – формирование личности ученика – осталась неизменной.
Современные педагоги в работе с детьми 21 века должны учитывать изменившиеся социально-культурные условия, такие как увеличение влияния средств массовой информации, появление молодёжных субкультур, направленных на получение удовольствия, нарастание межнациональных и напряжений и напряжений между поколениями. Именно поэтому стандарты второго поколения определяют приоритет в образовании именно воспитанию, которое является главным составляющим в процессе обучения и развития. Воспитание в школе должно осуществляться не периодически, а систематично, и пронизывать не только учебную деятельность, но и внеурочную. В базисном учебном плане выделены основные направления внеурочной деятельности:
- спортивно-оздоровительное
- художественно-эстетическое
- научно-познавательное
- военно-патриотическое
- общественно-полезное
- проектное
Эти направления можно реализовывать во время наиболее популярных форм внеклассной работы:
- математические кружки и творческие объединения интеллектуалов;
- факультативы и спецкурсы (элективные профильные курсы);
- олимпиады, конкурсы и викторины;
- математические олимпиады и вечера;
- математические дискуссии и диспуты;
- защита авторских проектов и рефератов;
- проектная деятельность;
- неделя математики и творческие дни юных математиков;
- школьная и классная математическая печать (включая и электронную);
10. изготовление и конструирование математических моделей;
11. математические экскурсии и научно-практические конференции.
Внеурочная деятельность может помочь развить различные способности ребёнка .
Развитие мышления. Если нам нужно выяснить, как и почему произошло некоторое событие, то что мы делаем?
1) Мы собираем информацию из различных источников.
2) Выдвигаем гипотезу: как и почему произошло данное событие.
3) Проверяем гипотезы.
4) Делаем выводы.
Развитие воли. Ребёнок должен учиться доводить начатое дело до конца и делать его как можно лучше.
Поведение в обществе и отношение к людям. Ребёнок должен знать, что существуют не только права, но и обязанности человека. Лучше начинать это знакомство в игровой форме.
Эмоциональность занятия. Имеется в виду не развлекательность урока, а эмоциональный подъём, которого должны достичь ученики, выполнив то или иное задание.
Умение адекватно оценивать свою работу и работу товарищей.
Развитие умения работать в команде. Дети должны понять, что в каком-то задании им удобнее объединить свои усилия. Например, у них разные элементы головоломки или недостаток жетонов для открытия задания.
Хорошее игровое занятие по математике предполагает:
1. возможность показать свои знания, поделиться ими с товарищами
2. совершить рискованный поступок
3. проявить умение нестандартно мыслить
4. в игре следует поощрять продвижение участников (на уроках учитель вынужден ограничивать активность: дай ответить другим)
5. различные способы достижения цели: каждый имеет право сам выбрать пути решения
К.псих. н., создатель методики «школа МиКЭБИ», Ю. Б. Гатанов, вслед за педагогом Карлом Витте утверждает, что «любой ребенок может стать гением, если его правильно развивать». В своей экспериментальной работе он пришёл к выводу о перспективности разработок игр-путешествий для учащихся. В играх-путешествиях дети не конкурируют друг с другом, а действуют в определенных исторических эпохах, соблюдая законы и культуру тех времен, «общаясь» с историческими и мифологическим персонажами, помогают одноклассникам, объединяются в группы для повышения эффективности своих действий [1, 2].
Урок- путешествие
- Сегодня мы с вами отправимся в древний Рим. Рассмотрим числовую ось. Что же это за дата – первый год? Существовал ли мир до этой даты? Люди разных стран договорились считать 1 год – годом рождения Христа. Всё время, которое было до этого, называется «до нашей эры», после – «наша эра»
Мы отправимся в далёкое прошлое (Дети закрывают глаза, учитель передвигает деление на 753 год до н.э. – год основания Рима, вывешивает картины, рисунки, создающие атмосферу Древнего Рима)
- Перед вами одна из наиболее могущественных и величественных античных цивилизаций, которая называется Древний Рим. В результате обманов и интриг сыновья троянского царя Энея, Ромул и Рем были выброшены в реку Тибр. Их вскормила волчица, а заботы матери заменили прилетевшие птицы, ставшие впоследствии священными животными для Рима. Что это были за птицы, мы узнаем, разгадав ребус:
1) 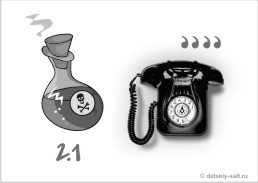
( Дятел)
2) Если дано СУММА и Мартышка, тогда 1+3=СУМКА,
Если дано ЛАПА и ПАНО, тогда 2+1=ПАПА,
Если дано КИРПИЧИ и БИССЕКТРИСА, тогда 3+1=… (ЧИБИС)
- Теперь мы знаем, какие птицы спасли Ромула и Рема от гибели, и можем отправляться дальше. Отомстив своему родственнику Амулию, братья решили основать город. По легенде, они не смогли договориться, на каком холме должен располагаться город, вспыхнула ссора, в ходе которой Ромул убил своего брата. Раскаявшись в убийстве Рема, Ромул основал город, которому дал своё имя (лат. Roma), и стал его царём.
- Теперь перенесёмся на 244 года вперёд, когда Рим становится республикой. Мы встречаем трёх путников, один из которых мудрец (всегда говорит правду), второй – болтун (всегда врёт), а третий – горожанин (может соврать, а может сказать правду).
Они сообщили нам:
А: В Риме было 9 царей, а я – горожанин.
В: Это правда.
С: В Риме было 7 царей, и я не горожанин.
Кто такие А, В, С и сколько в Риме было царей?
Решение: Прежде всего заметим, что A не может быть мудрецом, потому что мудрец не назвал бы себя горожанином. Следовательно, A - либо болтун, либо горожанин. Если В – горожанин, тогда правдиво высказывание путника B. Значит, B - либо мудрец, либо горожанин. Но B не может быть горожанином (так как горожанин – это А), поэтому B - мудрец, а C - болтун. Но болтун не может сказать о себе, что он не горожанин (так как любой болтун - не горожанин), и мы приходим к противоречию. Итак, A не может быть горожанином. Следовательно, A - болтун. Это означает, что высказывание путника B ложно, поэтому B должен быть горожанином (болтуном он быть не может, так как болтун - путник A). Итак, A - болтун, а B - горожанин. Отсюда следует, что С – мудрец, и в Риме было 7 царей.
Большой выбор заданий для внеклассных занятий по математике представлен в статьях к.п.н., доцента Горева П.М. [3], статьях и книгах Спивака А.В. [4, 5].
Жители Рима поделились на аристократов, или патрициев, и плебеев, которые им подчинялись. Аристократическое образование напоминало спартанское: особым вниманием к патриотизму, дисциплине, смелости и военному мастерству. В 287 г. до н.э. завершилась борьба патрициев и плебеев. Победа плебеев привела к изменению римского общества: они добились равноправия, знатные плебейские роды составили вместе со старыми патрицианскими родами новую элиту — нобилитет. Это способствовало ослаблению внутриполитической борьбы в Риме.
В 63 г. до н. э. великим понтификом (высшим жрецом) избирается Гай Юлий Цезарь. Обладая блестящими способностями стратега и тактика, стал единовластным повелителем Римской империи и подчинённых ею земель. Помня о неудачном правлении семи царей Рима, Цезарь стал пожизненным диктатором.
Цезарь даёт нам задание: нужно справиться с головоломкой Пифагора.
Головоломка Пифагора - это квадрат, разделенный на семь частей - 2 квадрата, 4 треугольника и параллелограмм. Изобразительные возможности игры достаточно велики - можно создавать силуэты различной степени сложности и сложные геометрические фигуры, напоминающие предметы быта, животных, птиц и т.д.
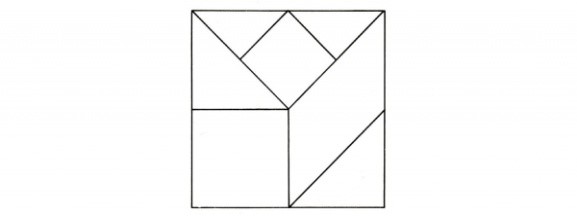
Возможные варианты фигур предложены ниже.
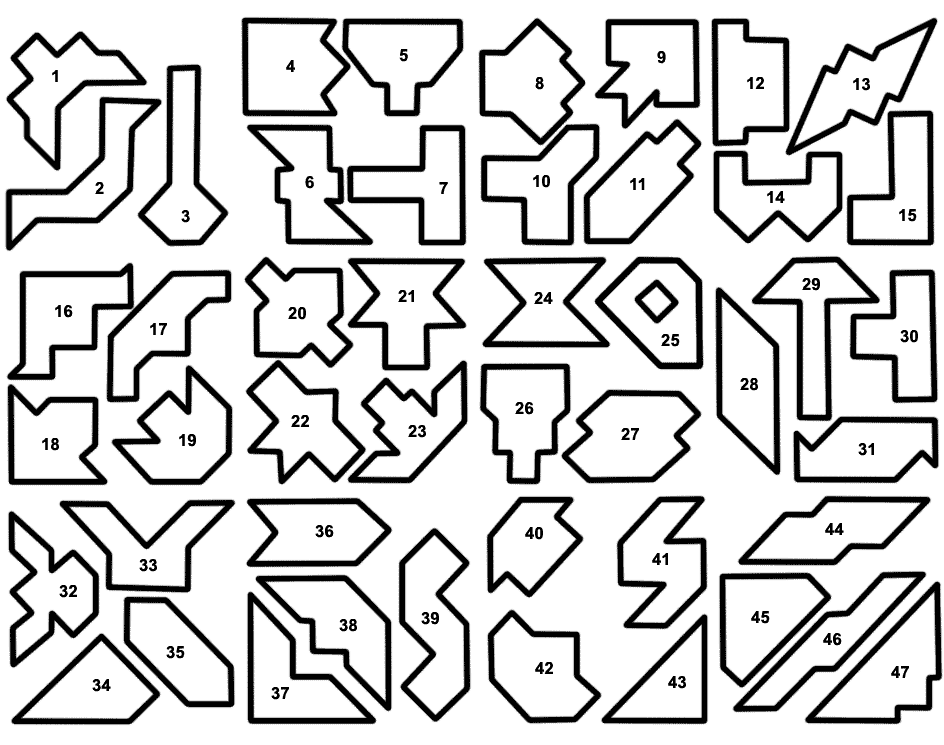
Пока дети складывают фигуры, учитель может коротко рассказать о реформах Цезаря.
- Две основные идеи реформ Цезаря заключались в необходимости объединения римского государства в единое целое, необходимости сгладить различия между гражданином-хозяином и его рабом, сгладить рознь национальностей. Вторая идея – тесное общение государства с подданными, сильная центрическая власть.
В Риме были очень популярны гладиаторские бои. Гладиа́тор (лат. gladiator — «меченосец», от gladius — «меч», «гладиус») — наименование бойцов, которые сражались между собой или с животными на забаву публике на специальных аренах. Сначала гладиаторские бои проводились на похоронах знатных людей – это было жертвоприношение в честь покойного, где воины в бою решали, кто из них станет жертвой. Мы жертвуем живыми, чтобы накормить мертвых» — так император Каракалла в III веке нашей эры сформулировал идейную основу гладиаторских боев. Кровавые сражения так пришлись по душе римлянам, что Цезарь повелел проводить бои на забаву зрителям. Бывали такие сражения, в которых принимали участие до 2 тыс. гладиаторов.
- Чтобы Цезарь подарил жизнь гладиаторам, мы должны пройти лабиринт.
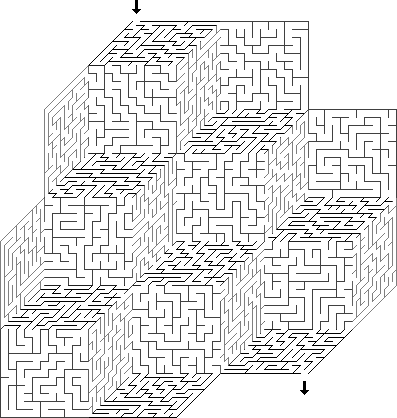
Для гладиаторских боёв был построен самый большой амфитеатр – римский Колизей – одна из главных достопримечательностей Вечного Города. Название «Колоссеум» он получил в XI веке за свои действительно колоссальные размеры – длина арены равна 85 метров, а ширина 53 метра. Амфитеатр вмещал почти 50 тысяч зрителей, которые поднимались на ярусы по 76 лестницам.
Следующее задание поможет нам вернуться в наше время. Для этого нам нужно превратить слово дом в слово Рим, меняя только одну букву за один ход. Ещё одно условие – нужно дойти до конца именно таким количеством ходов.
|
дом |
|
сом |
|
сок |
|
сук |
|
лук |
|
лик |
|
лис |
|
рис |
|
Рим |
В июне 455 г. н. э. вандалы захватили Рим и подвергли его страшному разгрому. Западно-римской империи был нанесен смертельный удар. Под властью Рима к началу 460-х осталась фактически одна Италия. 4 сентября 476 года Западная Римская империя прекратила свое существование. Восточная Римская империя просуществовала ещё 10 веков до 1453 года, когда империя окончательно распалась.
- Теперь нам пора домой. (Дети снова закрывают глаза, учитель передвигает деление на 2015 год – наше время). По возвращению нужно обсудить приключение.
- Что понравилось?
- Что нового узнали?
- Какие знания и умения нам пригодились?
На следующих занятиях дети знакомятся с историей других стран.
Такие занятия повышают критичность мышления, способность нестандартно мыслить, инициативность.
Для формирования творческого самостоятельного мышления необходимо:
1) Создать условия, которые обеспечивают высокую эмоциональность детей в учебном процессе (через создание проблемной ситуации, через понимание зависимости своих «выигрышей» от собственных знаний, умений, через внешнюю эффектность, которую создаёт атмосфера Древнего Рима и других стран: картины, музыка, связь заданий с историей)
2) Учитель не должен диктовать, указывать на этих занятиях, а должен лишь направлять мысль в нужное русло. Дети должны действовать сами, не рассчитывая не помощь учителя.
3) Поощрение нестандартности, продуктивности мышления.
Для развития каждого учащегося и формирования положительной и адекватной самооценки необходимо:
1. Создание условий, где для учащегося возможен свободный выбор задач разного уровня сложности;
2. Создание условий, где возможно получение консультации от одноклассника, от учителя, из других устных или письменных источников;
3. Каждый учащийся имеет право остаться при своем мнении и действовать так, как он считает нужным.
Соблюдение этих условий поможет добиться не только повышения заинтересованности математикой, но и развития умений активно работать, аргументировать свой ответ, применять свои знания на практике.
Ссылки на источники:
- Гатанов Ю.Б. Курс развития творческого мышления для детей 6-8 лет. - СПб: Иматон, 1999. – 59 с.
- Гатанов Ю.Б. Концепция МиКЭБИГорев П. М. Уроки развивающей математики в 5–6-х классах средней школы // Концепт. – 2012. – № 10 (октябрь). – ART 12132. – 0,6 п. л. – URL: http://www.covenok.ru/koncept/2012/12132.htm.
- Спивак А.В. Математический праздник. – М.: Бюро Квантум, 2004. – 288 с. (Библиотечка «Квант». Вып.88)
- http://mmmf.msu.ru/archive/19992000/spivak67/s_logika.html - Кружок А.В.Спивака /1999-2000/ Архив/ Малый мехмат МГУ

 Ю.
Г. Ерошина
Ю.
Г. Ерошина