Работа относится к области статистического моделирования, а именно к практике применения нелинейного регрессионного анализа, широко применяемого не только в естественных, но и в гуманитарных науках (лингвистика, социология, психология и др.).. В ней приводятся некоторые критические замечания к выбору пары кривых, применяемых в общепринятом алгоритме [1-4] такого анализа. Этот алгоритм приводится в учебниках [1,2], на материале из которых будет основываться дальнейшее изложение.
В [1] основное внимание уделено линейному регрессионному анализу. После введения в основные представления и определения, для двумерного случая линейного регрессионного анализа строится пара уравнений:
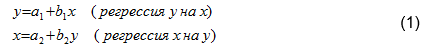
Далее, по формальной аналогии с (1), строится пара уравнений, используемых при (параболической) нелинейной регрессии:
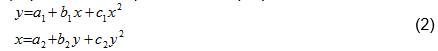
Выбор обоих уравнений в виде парабол [1-3] (в общем случае применяются многочлены одинаковой степени) и явился «камнем преткновения» для авторов. Такой выбор несколько не вяжется со свойствами и особенностями прямых, применяемых при линейном регрессионном анализе.
В работе [1] (стр. 48-49) подробно, на высоком методическом уровне отмечается, что, при линейном регрессионном анализе степень корреляции двух случайных величин зависит от коэффициентов b1и b2, (коэффициентов линейной регрессии). Это тангенсы углов наклона прямой у=а1+b1х к оси абсцисс (угол α) и прямой х=а2+b2у к оси ординат(угол β). Чем меньше величина угла γ (гамма) между указанными прямыми регрессии, тем больше связаны сравниваемые величины. На этом основании, сделан вывод, что “ для полной характеристики связи всегда необходимо знать оба коэффициента регрессии. Если угол γ=0 и обе линии регрессии сливаются в одну прямую, то by/x= 1 /bx/y, а связь между величинами становится функциональной. Если же линии регрессии параллельны осям координат и взаимно перпендикулярны, то зависимости между случайными величинами не существует”. В [1,2] указано, что несовпадение регрессионных кривых обусловлено стохастическим характером связи между случайными величинами и вызывается тем, что среди действующих на них факторов имеются как факторы, влияющие на обе связанные величины, так и факторы, влияющие только на величину Xи только на величину У.
Степень связи, можно, в случае линейной регрессии, характеризовать коэффициентом корреляции r, который выражается через тангенсы углов наклона прямых регрессии ![]() .
.
Заметим, что когда прямые совпадают, одна прямая регрессии связана с другой как обратная от нее функция. Очевидно, что и для нелинейной регрессии кривые регрессии совпадают (сливаются в одну кривую) когда они связаны как прямая и обратная функции. Но, для пары параболических линий регрессии, обратная к параболической функция, выражается через радикалы, то есть не является многочленом второй степени, как это постулируется в выражении (2). Тогда при предельной корреляции, то есть при функциональной зависимости между парой переменных, кривые регрессии не будут совпадать. (Совпасть могут только кривые двух функций, прямой и обратной к ней). В случае, когда по одной из кривых параболическая связь просматривается хуже, также может быть полезно использование пары взаимно обратных функций регрессии. Дело в том, что степень совпадения кривых регрессии зависит от степени действия на стохастическую связь переменных, влияющих только на хуже описываемую переменную, и не влияющих на другую. Представляется вероятным, что параболическая кривая хуже приближает истинную зависимость между переменными, чем функция, обратная к другой кривой регрессии (парной параболе, см(2)), которая лучше соответствует экспериментальным данным..
Конечно, в случае, когда нужно выявить просто какую либо нелинейную связь, достаточно воспользоваться парой зависимостей (2). Но в случае, если вид связи известен, например, из теории изучаемого явления, и корреляция не выявляется по одной из кривых регрессии, возможно для ее выявления может оказаться полезной проверка регрессионной кривой, которую нужно выбрать как кривую соответствующую зависимости обратной к другой кривой. При этом возможна наглядная линеаризация на некоторой подобласти задачи нелинейного регрессионного анализа, когда за прямые линейного анализа берутся касательные к линиям нелинейной регрессии. Это позволит правильнее оценить степень влияния различных факторов на рассматриваемую статистическую модель, а также воспользоваться преимуществами простоты и наглядности изложения, примененного в [1] при рассмотрении линейного регрессионного анализа, обеспечив тем самым и преемственность в изложении нелинейного регрессионного анализа с линейным случаем.
Таким образом, из вышеизложенного представляется полезным и обоснованным, наряду с принятой процедурой нелинейного регрессионного анализа, для получения дополнительной информации об используемой статистической модели, использовать еще две пары зависимостей вида прямая функция и обратная к ней, где прямыми функциями полагаются многочлены одинаковой степени в принятой процедуре регрессионного анализа, (например, параболы, из (2)).
Ссылки на источники:
- А.Б. Каждан, О.И. Гуськов, А.А. Шиманский. Математическое моделирование в геологии и разведке полезных ископаемых. М., Недра, 1979г., 168с.
- А.Е. Мартьянова. Математические методы моделирования в геологии. Часть 1, Астрахань, АГТУ, 2008, 218с.
- Гл. ред. И.М. Виноградов. Математическая энциклопедия т3., Москва, БСЭ, 1982, 592с.
- Г. Корн, Т. Корн “Справочник по математике для научных работников и инженеров”. М., Наука, 1984, 832с.

 Е.
В. Гусева
Е.
В. Гусева