Текстовые задачи занимают значительное место в школьной программе математики. Их особенностью является то, что они увязывают упрощенное описание действительности и ее математической модели. В процессе решения текстовых задач у учащихся формируется умение моделировать реальные объекты и явления. Разнообразие задач, встречающихся в школьном курсе математики, крайне велико. Для удобства выделяют следующие основные классификации текстовых задач по различным основаниям [1] (Рис. 1).
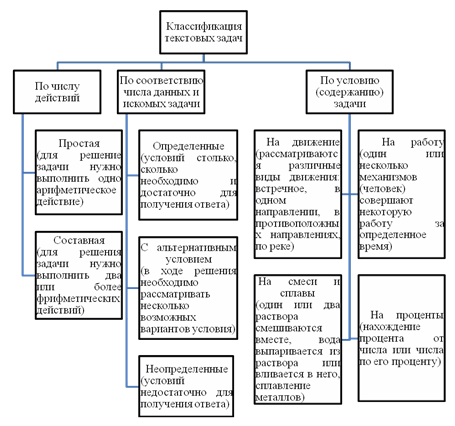
Рис.1. Классификация текстовых задач
В основу классификации кладутся следующие основные характеристики текстовой задачи: сложность задачи (количество выполняемых действий), определенность условий задачи и сюжетная фабула. Каждую отдельную задачу можно отнести к различным группам в зависимости от выбранной характеристики. Наибольшее количество различных видов задач выделяют по содержанию. Остановимся на данной классификации более подробно.
При решении подобных задач выделить ее вид в явном виде удается далеко не всегда, так как сюжетная составляющая весьма разнообразна. Кроме того, некоторые задачи могут содержать несколько сюжетных линий одновременно. В таких случаях говорят о комбинированных задачах. Тем не менее можно выделить отдельные, наиболее распространенные сюжеты. Чаще всего рассматривают задачи на работу, на движение, на проценты и отношения, на смеси и сплавы. Кроме того, можно выделить особую группу задач, которые встречаются в задании 17 ОГЭ. Это задачи с геометрическим содержанием. Их можно рассматривать и как текстовые, так как в условии задачи описана некоторая реальная ситуация. Однако в основу математической модели, которую необходимо построить при решении задачи, кладутся геометрические представления. В качестве примера рассмотрим следующую задачу: какой угол (в градусах) описывает минутная стрелка за 8 минут? [2]
Для начала найдем, сколько градусов описывает минутная стрелка за 1 минуту. Для этого градусную меру окружности поделим на общее число минут за полный оборот 360°:60=6°, тогда за 8 минут она опишет угол величиной 6*8=48°, . Таким образом, за 8 минут минутная стрелка опишет угол в 48°. Как видим, в данной задаче рассматривается реальная ситуация, при этом для решения данной задачи необходимы знания о том, что окружность составляет 360°, то есть геометрического характера.
Среди различных сюжетных линий особые трудности у учащихся при решении текстовых задач ОГЭ вызывают задачи на совместную работу, на движение и на смеси и сплавы. При построении математической модели задач такого типа возникают сложности с установлением взаимосвязей между заданными в условии величинами. Школьники далеко не во всех случаях ясно понимают суть и природу таких связей. Формальное знание основной формулы, например, что скорость есть отношение пройденного пути ко времени его прохождения, не позволяет ее использовать во всех встречающихся в задачах ситуациях.
Как следствие возникают затруднения при выборе неизвестных величин, выражении одних неизвестных через другие величины (известные и неизвестные). В конечном итоге учащиеся не могут составить уравнение и систему уравнений, приводящую к решению задачи. А именно эти этапы в решении текстовых задач в большей степени способствует развитию мышления учащихся. Для более ясного понимания учащимися особенностей математических моделей, встречающихся при решении задач, в учебном процессе достаточно часто использую специальные схемы, графики, таблицы. Их применение позволяет более наглядно выявить взаимосвязи между отдельными элементами, представить их в удобной для восприятия и запоминания форме.
Рассмотрим пример решения текстовой задачи на движение [3]. Моторная лодка прошла против течения реки 60 км и вернулась в пункт отправления, затратив на обратный путь на 45 минут меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.
Примем за км/ч скорость лодки в неподвижной воде. Зная, что скорость течения реки равна 2 км/ч, найдем скорость лодки при движении. Ее скорость по течению реки будет составлять км/ч, а против течения – км/ч. И по течению и против течения лодка прошла 60 км. Для более наглядного представления условий задачи составим таблицу, определяющую соотношения между скоростью, пройденным расстоянием и затраченным временем (табл. 1).
Таблица 1.
Вспомогательная таблица для решения текстовой задачи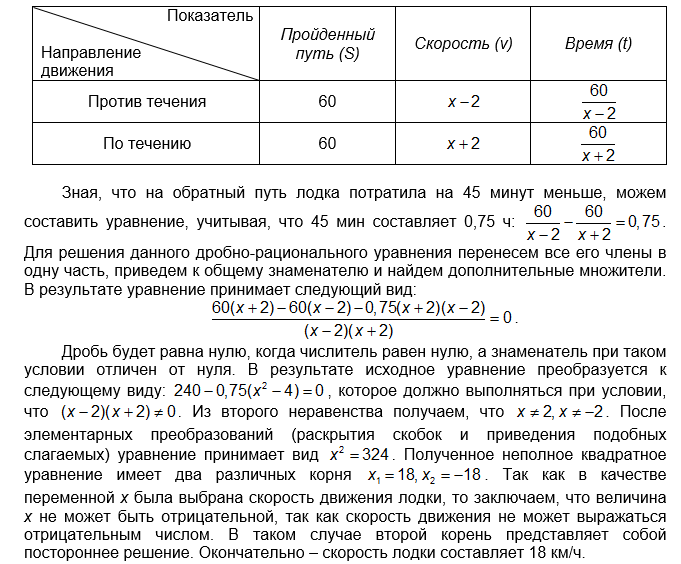
Применение специальных средств (например, таблиц взаимосвязей между объектами задачи) позволяет лучше увидеть логику отношений между ними. Текстовые задачи часто вызывают затруднения у учащихся, поэтому следует уделять их решению больше времени, проводить по возможности элективные курсы, факультативы, выполнять задания на уроках на развитие логики, объяснять основные моменты решения таких задач. Кроме того, такие вспомогательные средства позволяют не пропустить основные этапы решения задачи и представить их в более наглядной форме.
Сформированность у учащихся представления о способах и методах решения задач обеспечивает их продуктивную работу в ходе поиска ответа на требования задачи, что способствует набору большего количества баллов при сдаче ОГЭ.

 Н.
В. Леонтьева
Н.
В. Леонтьева