Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения ( Л.М. Фридман, Е.Н. Турецкий) [3].
Часто в методике их смешивают с задачами повышенной сложности. Задачи повышенной сложности содержит условие, которое помогает обучающимся выявить математический аппарат, необходимый для решения задачи в начальной школе. Учитель может, контролирует процесс закрепления знаний, предусмотренных программой обучения решением задач повышенной сложности. Решение нестандартной задачи предполагает от учащихся проведение исследования. В тоже время, если решение одной и той же задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методом его решения , то для другого ученика – решение этой же задачи происходит стандартным образом, так как он уже умеет решать такие задачи. Одна и та же задача по математике в начальной школе может быть нестандартной, а в основной школе она уже является обычной, то есть не повышенной сложности.
Таким образом, если учащийся при решении задач не знает способ решения и не опирается на теоретический материал, то в этом случае задачу можно назвать нестандартной на данном периоде обучения.
На современном этапе обучения в начальной школе знакомят учащихся с нестандартными видами задач как на уроке, так и внеурочное время.. Объясняется это, прежде всего, возрастающими требованиями, направленными на усиление развивающих функций обучений.
Многие методисты используют понятие«нестандартная задача». Ю. М. Колягин определяет таким образом: «Под нестандартной понимается задача, при предъявлении которой учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение» [1].
Анализ методической литературы позволил выявить роль использования нестандартных задач в практике обучения математике, а также установил их общую и специфическую роль.
Нестандартные задачи: учат обучающихся применять не только готовые алгоритмы, но и самостоятельно находить новые способы решения этих задач, т. е. способствуют умению находить нестандартные способы решения задач; оказывают влияние на развитие смекалки, сообразительности обучающихся; препятствуют использованию штампов при решении задач, разрушают неправильные ассоциации в знаниях и умениях учащихся, предполагают не столько усвоение алгоритмических приемов, сколько нахождение новых связей в знаниях, к переносу знаний в новые условия, к овладению разнообразными приемами умственной деятельности; создают благоприятные условия для повышения прочности и глубины знаний учащихся, обеспечивают сознательное усвоение математических понятий.
При обучении решению нестандартных задач учитель должен:
- давать готовые алгоритмы;
- сюжет должен быть доступен всем учащимся;
- сюжет должен быть интерес для данного возраста;
Некоторые виды нестандартных математических задач, которые рассматриваются в начальном курсе математики:
1 Логические задачи (которые рассматриваются в курсе математической логики) сложно разграничить с текстовыми задачами, решаемыми логическим методом, так как большинство из них можно отнести и к тем и к другим.Под логическими задачами будем понимать такие задачи, для решения которых, как правило, не требуется выполнение вычислений, а используются лишь логические рассуждения.
1.1 Задачи на переливание. К задачам этой группы относятся задачи, в которых требуется, как правило, разлить заданное количество жидкости по имеющимся сосудам так, чтобы получить требуемое количество жидкости либо в каждом сосуде, либо в некоторых из них. При этом пользоваться можно только сосудами известной вместимости, которые есть в наличии.
1. Имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из водопроводного крана 7 л воды?
2. Как, имея лишь два сосуда 5 л и 7 л, налить из водопроводного крана 6 л воды?
1.2 Задачи на взвешивание. К задачам этой группы относятся задачи, в которых за минимальное число взвешиваний требуется:
а) определить среди имеющихся монет (или деталей) фальшивую (она по массе отличается от настоящих);
б) расположить предметы в порядке убывания (возрастания) их массы;
в) выразить массу одних предметов через массу других.
1. У хозяйки есть рычажные весы и гиря в 100 г. Как за 3 взвешивания она может отвесить 700 г крупы?
2. Три одинаковых яблока тяжелее, чем четыре одинаковые груши. Что тяжелее: 4 яблока или 5 груш?
1.3 Задачи на переправы. К задачам этой группы относятся задачи, в которых рассматриваются всевозможные затруднительные ситуации, когда при определенных обстоятельствах требуется некоторой группе людей переправиться самим с одного берега на другой, либо переправить некоторые одушевленные и неодушевленные предметы. При этом трудности переправы обычно связаны с недостатком плавательных средств (одна лодка), с количеством и особенностями пассажиров и перевозимого груза.
1. Как-то раз крестьянин подошел к реке с пойманным волком, козой и капустой. Но вот беда – в лодку помимо крестьянина (а только он умеет грести) влезает либо только волк, либо только коза, либо только капуста. Кроме того, оставить без присмотра волка с козой или козу с капустой – верный способ потерять часть имущества. Как крестьянину переправиться вместе со своим имуществом без потерь?
1.4 Задачи на разъезды. К задачам этой группы относятся задачи, в которых рассматриваются всевозможные затруднительные ситуации, когда при определенных обстоятельствах некоторой группе транспортных средств в ходе их движения требуется в стесненных условиях разъехаться, чтобы продолжить движение, либо совершить некоторые маневры.
1. Поезд Б приближается к станции железной дороги, но его нагоняет быстрее идущий поезд А, который необходимо пропустить вперёд. У станции от главного пути отходит боковая ветка, куда можно отвести на время вагоны с главного пути, но ветка эта настолько короткая, что на ней не помещается весь поезд Б.
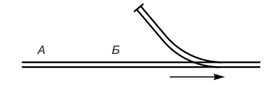
Спрашивается, как всё-таки пропустить поезд А вперёд?
1.5 Задачи на дележи. К задачам этой группы относятся задачи, в которых требуется некоторым образом без подручных средств разделить имеющиеся предметы между несколькими лицами.
1. Три одинаковых арбуза надо разделить поровну между 4 людьми. Как по-разному это можно сделать? Какое количество разрезов нужно сделать в каждом случае?
2. Требуется разделить 5 одинаковых яблок поровну между восемью мальчиками. Найдите 2-3 способа сделать это. Как это сделать с наименьшим числом разрезов?
1.6 Задачи на соответствие и порядок. К задачам этой группы относятся задачи, в которых требуется либо установить соответствие между элементами двух и более множеств, либо установить соответствие между элементами данного множества и отрезком натурального ряда.
1. Три подруги вышли в белом, зеленом и синем платьях и в туфлях таких же цветов. Известно, что только у Ани цвет платья и цвет туфель совпадают. Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель на каждой из подруг.
2. Жили три друга: учитель, врач и рабочий. Их фамилии Борисов, Иванов и Семенов. У учителя нет ни братьев, ни сестер, он самый младший из друзей. Семенов старше врача и женат на сестре Борисова. Назовите фамилии учителя, врача и рабочего.
1.7 Истинностные задачи – это задачи, в которых требуется установить истинность или ложность высказываний.
1. Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего – Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Леший, кто украл Василису?
1.8 Задачи на распиливание, разрезание и сводимые к ним задачи.К задачам этой группы относятся задачи, в которых требуется некоторым образом без подручных средств распилить или разрезать на необходимое количество частей удовлетворяющих определенным условиям задачи имеющиеся предметы
1. Имеются бревна длиной 4 м и 5 м одинаковой толщины. Бревно перепиливается за 1 минуту. Надо напилить 20 бревен длиной 1 м. можно пилить только 4-метровые или только 5-метровые бревна. Какие бревна надо пилить? Почему?
2. Пильщики распиливают бревно на метровые обрубки. Длина бревна 5 м. Распиловка бревна поперек отнимает каждый раз 1 минуты времени. За сколько минут распилили они все бревно?
1.9 Задачи на принцип Дирихле. В простейшем виде этот принцип формулируется следующим образом: «Если десять рыбок находятся в девяти аквариумах, то в некотором аквариуме находятся не меньше двух рыбок».
Общая формулировка: «Если, а рыбок находиться в k аквариумах, то найдётся аквариум, в котором находится не меньше чем, а/k рыбок, и найдётся аквариум, в котором находится не больше чем, а/k рыбок».
Решение задачи будет дробное число рыбок – если получится, что в аквариуме не меньше 7/3 рыбок, значит, их не меньше трёх.
а) В первенстве по футболу участвует 18 команд. Первенство разыгрывается в один круг, любые две команды встречаются только один раз. Известно, что каждая команда сыграла какое-то число игр. Докажите, что найдутся две команды, сыгравшие одинаковое число игр.
б) В городе живет 200 тыс. жителей. Докажите, что в городе найдутся хотя бы 2 человека с одинаковым числом волос на голове. Считайте, что у человека на голове не больше 150 тыс. волос.
2 Геометрические задачи:геометрические головоломки, геометрия в пространстве, геометрия на клетчатой бумаге. Это такие задачи, решение которых базируется на основных понятиях планиметрии, свойствах плоских фигур и логических рассуждениях, либо практических действиях.
3 Нестандартные арифметические задачи – это текстовые задачи, в которых требуется найти значение некоторой величины с помощью арифметических действий над числами и для которых в курсе математики начальной школы нет общих правил и положений, определяющих решение.
Е.Е. Останина выделяет виды таких задач по способам или приемам которые помогают решить такие задачи: построение рисунка или чертежа, введение вспомогательного элемента (части), использование способа подбора, переформулировка задачи, для того чтобы она стала знакомой и понятной, разделение на части условия или вопроса задачи и решение задачи по частям, решение задачи начиная «с конца» [2].
4. Комбинаторные задачи - это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа. Выделяют комбинаторные задачи на правило суммы, правило произведения и виды комбинаций: сочетания, размещения, перестановки. Методы решения комбинаторных задач: перебор хаотичный и систематический (с помощью выбранного алгоритма, с помощью построения таблиц, графов и разновидности графов дерева возможных вариантов) с помощью правил и формул для подсчета числа различных видов комбинаций.
Знакомство в начальной школе с комбинаторно-вероятностными понятиями имеет следующие особенности:
1) в понимании учащимися случайных процессов присутствует значительная доля бессознательного и интуитивного;
2) способность обучаемых характеризовать их только качественно;
3) необходимость опоры на жизненный опыт младших школьников;
4) длительность формирования соответствующих когнитивных структур в неразрывной связи с приобретаемыми в начальной школе знаниями, умениями и навыками.
5. Простейшие задачи вероятностного содержания.
Можно выделить четыре типа задач вероятностного содержания для учащихся начальной школы. Первый тип заданий – на классификацию событий, второй типа - об исходах в испытаниях, задачи третьего типа - сравнение вероятности появления события, задачи четвертого типа – на определение вероятности события (относительной частоты события). Задачи четвертого типа имеют знак *, обозначающий задачи повышенной сложности, необязательные для решения всеми учащимися.
Существуют ли методы обучения решению задач в начальной школе по математике, которые мы являются нестандартными? Наверно универсального метода нет. Научить младших школьников решению нестандартных задач возможно, если вызвать интерес у учащихся к их решению, предложить интересные и содержательные по сюжету задачи, для современного ученика. Или же заменять формулировку вопроса, используя проблемные жизненные ситуации. Например, вместо задания «решить Диафантово уравнение», предложить решить следующую задачу. Может ли ученик расплатиться за покупку стоимостью 1900 рублей, если у него только сторублевые купюры, а у продавца – десятирублевые?
Умение решать нестандартные задачи приобретается практикой. Не зря говорят, что математике нельзя научиться, глядя, как это делает сосед. Самостоятельная работа и помощь учителя – вот залог плодотворной учебы.
Наблюдения показывают, что математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив учащихся владеть умением решать задачи, мы окажем существенное влияние на их интерес к предмету, а также на развитие познавательных универсальных учебных действий у них.

 А.
К. Мендыгалиева
А.
К. Мендыгалиева