Плазменное напыление является одним из перспективных технологических методов получения, упрочняющих, износостойких, восстановительных, защитных и декоративных покрытий. Однако внедрению на большую часть государственных производственных предприятий этого метода препятствует ряд проблем, обусловленных отсутствием системы управления качеством плазменных покрытий, а также утвержденной на постоянной основе и учитывающей все факторы, влияющие на процесс нанесения плазмы, математической модели.
Как известно, основными технологическими параметрами, определяющие свойства покрытий, являются величина тока дуги плазматрона, а также расход и состав плазмообразующего газа. В связи с этим построение математической модели является важным этапом выбора режима напыления и управления процессом [1].
Расчет температуры частиц при плазменном напылении необходим, так как температура является основополагающим фактором при определении свойств покрытия, таких как прочность сцепления, когезионная прочность, пористость и т.д. Также температуру можно регулировать в широких пределах с помощью изменения технологических параметров. Как известно, подбор режимных параметров напыления весьма сложный процесс, при котором для каждого определенного материала подбираются конкретные данные.
При построении математической модели процесса плазменного напыления были выделены основные его стадии, которые изображены на рисунке 1.
На каждой приведенной стадии производят следующие необходимые расчеты:
1) По значениям I, расхода G и состава С плазмообразующего гага рассчитывают удельную энтальпию газа Hуд0.
2) Вычисляют температуру Т0и скорость струи v0.
3) Рассчитывают температуру Тs (x) и скорость струи vs (x)на разных расстояниях от среза сопла плазматрона.
4) Вычисляют свойства плазмообразующего газа.
5) Определяют скорость напыляемых частиц vч (x).
6) Рассчитывают температуру частиц Тч (x) на разных расстояниях от среза сопла плазмотрона.
7) Находят зависимость пористости покрытия П и коэффициента использования материала от температуры и скорости частиц.
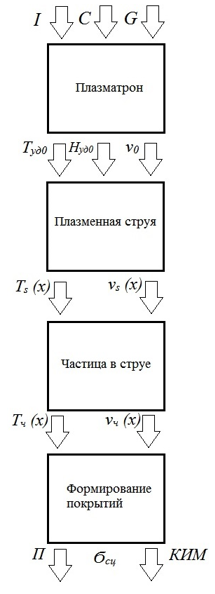
Рис. 1. Стадии процесса плазменного напыления при формировании математической модели
Учитывая математические основы описания напряженно-деформированного состояния материалов при формировании покрытий, а также основы тепловых процессов с учетом температурного расширения, математическое моделирование процесса можно представить в виде следующих этапов [2]:
1) Моделирование движения и нагрева частиц порошка в плазменной струе.
2) Моделирование тепловых процессов и термических напряжений в системе покрытие – подложка.
3) Математическое описание растекания расплавленной частицы после соударения с твердой подложкой.
4) Моделирование размерного формообразования при нанесении покрытий.
Важным аспектом при построении математической модели процесса плазменного напыления является описание плазматрона. Необходимо определить взаимосвязь тепловых и энергетических характеристик плазматрона с удельной энтальпией газа Hуд0, скоростью и температурой плазменной струи. На рисунке 2 изображен самый популярный плазматрон 3MB фирмы Sulzer Metco, который, с небольшими модификациями, существует уже больше 40 лет.
Еще одним аспектом при построении математической модели технологии плазменного напыления является расчет тепловых и динамических параметром плазменной струи. Так как строгой теории расчета параметров плазменной струи не описано, то её условно можно разбить на три участка: начальный, переходный и основной. После этого произвести необходимые расчеты.

Рис. 2. Плазматрон 3МВ
Также стоит учитывать термодинамические и переносные свойства плазмообразующих газов. При напылении обычно используют аргоноазотную смесь, хотя в последнее время все чаще применяют воздух [1].
Помимо перечисленных аспектов математического моделирования процесса плазменного напыления необходимо производить расчеты параметров частиц в плазменной струе, таких как, температура напыляемых частиц и скорость напыляемых частиц, которая определяется по формуле (1):
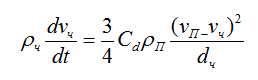 (1)
(1)
где ρч, vч, dч – плотность, скорость и диаметр частиц соответственно; ρП, vП – плотность и скорость плазменной струи соответственно; Сd – коэффициент гидродинамического сопротивления.
Полученные закономерности и связи между факторами и критериями процессов в ходе составления математической модели позволят решить оптимизационные задачи при разработке технологических рекомендаций и послужат основой в выработке новых способов нанесения плазменных покрытий [3].

 Г.
И. Трифонов
Г.
И. Трифонов