Геометрический материал на уроках математики в начальной школе изучается не обособленно, а совместно с арифметическим и алгебраическим материалами. С самых первых уроков учащиеся знакомятся с моделями геометрических фигур (треугольник, квадрат, круг, прямоугольник), а затем и с отдельными элементами этих фигур. Они широко используются при обучении счету, сравнении предметов и групп предметов, составов чисел, сравнении целых неотрицательных чисел. С.С. Мазалова отмечает, что «обновление содержания курса «Математики» идет за счет обогащения его сведениями из различных математических дисциплин (арифметики, алгебры, геометрии, логики) с целью установления перспективы математического образования и формирования готовности к систематическому изучению алгебры и геометрии в основной школе. Принципом реализации деятельного подхода является предъявление материала дискуссионного характера, когда учащиеся в процессе учебного диалога определяют способ построения учебной задачи, обсуждают алгоритм ее решения. Такой подход позволяет существенно уровень математического образования школьников, развить их мышление и воспитать устойчивый интерес к занятиям математикой»[1].
Модели различных симметричных фигур являются полезным дидактическим материалом при изучении долей и дробей. Геометрические модели оказывают неоценимую помощь в продумывании и поиске решения многих текстовых задач. Формирование навыков измерения, вычисление периметров и площадей фигур способствуют установлению отношений между фигурами и числами, а также выработке вычислительных навыков.
Изучение геометрического материала также как и арифметического сопровождается выполнением учебных заданий.
Выделим задания с геометрическим содержанием, рассматриваемых в начальной школе.
- Учебные задания на узнавание фигур.
- Учебные задания на измерение.
- Учебные задания на вычерчивание и построение.
- Учебные задания на нахождение и выделение фигуры в сложном чертеже.
- Учебные задания на видоизменение заданной фигуры.
- Учебные задания на сравнение фигур.
- Учебные задания на классификацию фигур.
- Задачи на вычисление.
Знакомство с геометрическими фигурами учащиеся начинают с узнавания и из различения. Сначала детям предлагают выбрать одинаковые фигуры, а затем – фигуры одинаковой формы не зависимо от их величины. Дети запоминают названия простейших фигур, учатся правильно называть и изображать их.
Задание 1
В лесной школе белочка и заяц начертили по одной фигуре каждый. Эти фигуры были разными. Зайка не стал чертить![]() . Белочка не стала чертить
. Белочка не стала чертить ![]() и
и ![]()
Кто какую фигуру начертил?
Уже в 1 классе дети овладевают навыком измерения отрезков, сравнения этих отрезков опираясь на результаты измерений.
Задание 2
На сколько красный отрезок короче синего? (рис. 1)
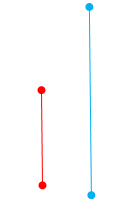 Рис. 1
Рис. 1
Использовать измерение длин отрезков возможно и при определении периметров многоугольников.
Задачи на построение требуют от учащихся некоторых умений в обращении с чертежными инструментами, поэтому следует ознакомить учащихся с правилами обращения с линейкой, циркулем, угольником. Упражнения на построение начинают с простейших: провести прямую линию, отложить отрезок на прямой линии, построить окружность произвольного радиуса, заданного радиуса, построить прямой угол, прямоугольник и т.д.
Задание 3
Начертите в тетради такие же фигуры (рис. 2):

Рис. 2
Проведи в каждой из них по два отрезка так, чтобы, разрезав по ним, можно было
получить два треугольника и один четырехугольник.
Особо обращается внимание на деление отрезков на 2, 3, 4, 5 и т.д. частей на глаз с последующей проверкой измерением, а также учащиеся начальной школы знакомятся с делением отрезка пополам при помощи циркуля и линейки.
Важно, чтобы дети умели видеть в сложном геометрическом чертеже все разнообразие фигур и их элементов, включенных в него.
Задание 4
Сколько треугольников на чертеже? Сколько квадратов? (рис. 3)
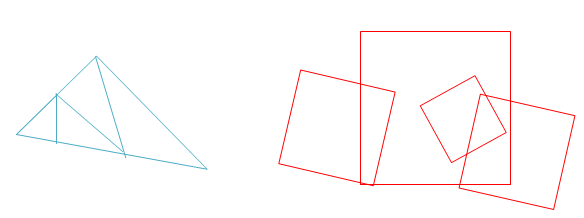
Рис. 3
Следует обратить внимание и на задания на видоизменение фигур наряду с заданиями на нахождение и выделение фигур. Для развития пространственного мышления первые служат непосредственным продолжением вторых.
Знакомство с детей с задачами на видоизменение фигур обычно начинают с упражнений на моделях фигур. Например:
- Прямоугольник или квадрат разрезать так, чтобы получить два треугольника.
- Отрезать от прямоугольника квадрат.
- Разрезать квадрат на части так, чтобы их них можно было составить прямоугольник.
- Разрезать треугольник так, чтобы из его частей можно было бы составить четырехугольник, прямоугольник.
Задание 5
- Рассмотри первый чертеж (рис. 4). Какая фигура дополняет четырехугольник до треугольника?
- Рассмотри второй чертеж. Подумай, как можно этот четырехугольник дополнить до треугольника. Сделай это в тетради.
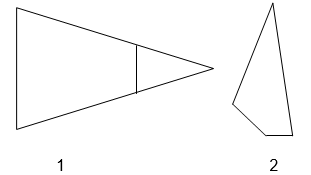
Рис. 4
Учебные задания по классификации геометрических фигур начинаются уже на первых этапах работы с геометрическим материалом. При анализе таких заданий следует обращать внимание учащихся на то, чтобы они рассматривали особенности не только фигуры в целом, но и свойства элементов данной фигуры, сопоставляя эти элементы между собой и с аналогичными элементами в других фигурах.
Задание 6
Разбей фигуры на две группы (рис. 5).

Рис. 5
Задания по классификации фигур приводят к сравнению одной фигуры с другой. Сравнение вызывает необходимость сопоставлять число содержащихся в фигуре элементов и размеры сходных элементов.
При сравнении фигур следует руководствоваться определенным порядком:
- выяснить, равно ли число сходных элементов данных фигур;
- установить соотношение между сторонами рассматриваемых фигур;
- узнать каково соотношение углов сравниваемых фигур.
При этом в начальной школе соотношение между линейными элементами фигур следует устанавливать посредством измерения линейкой, полоской бумаги, шнуром или циркулем. Соотношения между углами - посредством сравнения с углами чертежного треугольника.
Задание 7
Сравни фигуры на 1 чертеже с фигурами на 2 чертеже (рис. 6):
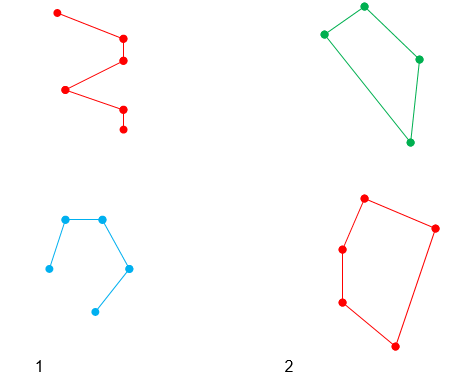 Рис. 6
Рис. 6
Решение геометрических задач вычислительного характера во многом сходно с решением арифметических задач.
Задание 8
Андрей от своей квартиры до школы может пройти двумя дорогами. По первой он идет до магазина 110 м и от магазина до школы 170 м , по второй – от квартиры до кинотеатра 140 м и от кинотеатра до школы 120 м. какой путь короче и на сколько? Начертите эти дороги одну под другой, каждую в виде двух отрезков, приняв 10 м за 1 клеточку.
Задание 9
Длина одного отрезка составляет 18 см. Другой отрезок короче первого в 3 раза. Найти общую длину двух отрезков.
Задание 10
Периметр прямоугольника 206 м. Одна сторона его 38 м. Найти другую сторону прямоугольника.
Поиск решения геометрических задач на вычисление ничем не отличается от разбора арифметических задач.
Таким образом, работа над учебными заданиями с геометрическим содержанием на уроках математики в начальной школе является средством развития пространственного мышления, а также формирования универсальных учебных действий.

 Р.
Ф. Швецова
Р.
Ф. Швецова