Полный текст статьи
Шехирева Елена Ивановна,
учитель математики, заместитель директора по УВР МОАУ «Лицей № 21», г. Киров
Липатникова Валентина Александровна,
учитель биологии МОАУ «Лицей № 21», г. Киров
Аннотация. Статья посвящена вопросам установления межпредметных связей между некоторыми темами, изучаемыми в школьных курсах математики, химии, биологии и экологии. В ней описываются отдельный математические модели, применяемые в естествознании. Приводятся отдельные примеры.
Ключевые слова: обучение математике, обучение естествознанию, математика в классах химико-биологического профиля, межпредметные связи.
Анализ современных программ и учебников позволяет сказать, что во многих из них в должной мере не реализована идея межпредметных связей, которая необходима для формирования системных знаний учащихся. Следует особо отметить, что с накоплением знаний и дифференциацией наук будет увеличиваться опасность изучения предметов вне их естественной взаимосвязи. Чтобы ликвидировать разрыв между отдельными учебными дисциплинами, нужно определить такое обучение, при котором предметы дополняли бы друг друга, опирались бы один на другой с целью успешного изучения и проведения анализа изучаемых событий, явлений и законов на основе современных достижений науки. В конечном итоге такое обучение поможет выработать у учащихся умения и навыки рассматривать изучаемые явления во взаимозависимости и взаимосвязи.
Вышеизложенное и составило основу реализации идеи межпредметных связей математики, химии и биологии.
Установление межпредметных связей на уроках математики
Для того, чтобы возникла математика как наука, человек в течение многих веков изучал окружающую действительность, устанавливал связи, закономерности и лишь тогда формулировал законы, которым подчиняется живая и неживая природа, а затем развитие математики позволило решать задачи из разных областей знаний с помощью построения их математических моделей. Вот такой двухсторонний процесс следует показывать учащимся при изучении математики.
Особенно благоприятно такое обучение математике в классах химико-биологического профиля. Красота форм, встречающаяся в природе, привлекает человека и, говоря словами немецкого биолога Э. Геккеля, «природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные человеком формы». Существа, рассмотренные в книге Э. Геккеля «Красота форм в природе» красивы и симметричны, рассмотрение их на уроках математики при изучении тем «Симметрия» и «Золотое сечение» является целесообразным.
Формы и явления, встречающиеся в живой и неживой природе, не случайны. Одноклеточный организм феодария точно передает форму икосаэдра. Это объясняется тем, что из всех многогранников с таким же количеством граней именно икосаэдр имеет наибольший объем и наименьшую площадь. Это геометрическое свойство помогает морскому микроорганизму преодолевать давление водной толщи. Использование золотой пропорции помогло природе приспособить организмы к выживанию во внешней среде и оптимизировать их работу. Для оптимального использования воска пчела строит соты в форме правильной шестиугольной призмы.
Рассмотрение примеров рационального использования природой своих ресурсов является хорошей мотивацией к обучению математике учащихся химико-биологических классов, в частности к решению задач на отыскание наибольших и наименьших значений величин с помощью свойств производной.
Как располагать своими средствами для получения наибольшей выгоды – это важная задача для всей практической деятельности человека. С такими задачами приходится иметь дело представителям самых разных специальностей, в том числе и химикам.
Для того, чтобы учащимся показать, как применяются математические методы в химии, можно предложить решить следующую задачу.
Задача. В каком из хлорпроизводных предельных углеводородов процент (массовая доля) хлора максимальный?
Решение. Пусть k – количество атомов хлора (Cl), CnH2n+2 – общая формула предельных углеводородов. Уравнение: CnH2n+2 + kCl2 = CnH2n+2 = CnH2n+2–kClk + kHCl, где 1 ≤ k ≤ 2n+ 2, n > 0, n – натуральное. M(CnH2n+2–kClk) = M(Cl)∙k + M(C)∙n + M(H)∙(2n – 2 + k) – молярная масса вещества. ω(Cl) = (M(Cl)∙k) : M(Cl)∙k + M(C)∙n + M(H)∙(2n – 2 + k) – формула массовой доли. Подставив значения в формулу, получим: ω(Cl) = 35,5k : (12n + 2n + 2 – k + 35,5k). Рассмотрим функцию y(k) = 35,5k : (14n + 2 + 34,5k). Найдём её производную: y’(k) = (497n + 71) : (34,5k + 14n + 2)2. Так как n - натуральное, то производная всегда положительна, а значит, функция возрастает на всей своей области определения, в том числе на промежутке [1; 2n + 2], следовательно при значении k = 2n + 2 значение функции будет максимальным. Подставим 2n + 2 в исходную формулу CnH2n+2–kClk, получим CnCl2n+2, при наименьшем n = 1, получаем: хлорпроизводным предельным углеводородом с максимальным содержанием хлора является вещество CCl4 (его массовая доля ω(Cl) = 92,2%, а в следующем представителе C2Cl6 массовая доля хлора ω(Cl) = 89,9%).
Ответ. Хлорпроизводным предельным углеводородом с максимальным содержанием Cl является вещество CCl4.
Учащиеся химико-биологических классов без труда справляются с данной задачей.
Вещество CCl4 называется тетрахлорметан, модель его молекулы представляет собой правильный тетраэдр – это еще один повод вернуться к связям между математикой и химией.
Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли (NaCl), монокристалл алюмокалиевых квасцов KAl(SO4)2∙12Н2О имеет форму октаэдра, кристалл сернистого колчедана FeS имеет форму додекаэдра, сурьмянистый сернокислый натрий – тетраэдра, бор – икосаэдра. Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ.
Перечисленные выше и другие факты позволяют установить зависимость свойств химических веществ от числа симметрий правильных многогранников, составляющих их макроструктуры.
Таким образом, можно сделать вывод: чем более высокой симметрией обладают макроструктуры веществ, тем эти вещества прочнее, более блестящие, тем выше у них температуры кипения и плавления, лучше теплопроводность.
Установление межпредметных связей на уроках биологии
В современной биологии активно используются различные разделы математики: теория вероятностей и статистика, теория дифференциальных уравнений, теория игр, дифференциальная геометрия и теория множеств для формализации представлений о структуре и принципах функционирования живых объектов.
Многие ученые высказывали мысль о том, что область знаний становится наукой только тогда, когда выражает свои законы в виде математических соотношений. В биологии, для которой предметом изучения являются индивидуальные живые системы, дело обстоит сложнее. Только в ХХ веке появились экспериментальные биохимия, биофизика, молекулярная биология, микробиология, вирусология, которые изучают воспроизводимые явления и активно используют физические, химические и математические методы.
В связи с индивидуальностью биологических явлений говорят именно о математических моделях в биологии (а не просто о математическом языке).
Математические модели в генетике популяций и в теории эволюции
Эволюционный процесс можно рассматривать как процесс видового обучения или как процесс поиска оптимального состояния. При этом популяция выступает как регулируемая многопараметрическая система. Кроме того, эволюция может рассматриваться и как процесс группового поведения автоматов. С этой точки зрения, популяция – это совокупность «автоматов» (организмов), которые, взаимодействуя между собой и с внешней средой, решают свои собственные локальные задачи. Однако в результате такого взаимодействия система в целом решает некоторую интегральную задачу, например, приспособления вида к новой среде обитания. Ясно, что в данном случае речь идет о примере управления за счет локальных взаимодействий, так как у популяции нет централизованного управляющего механизма.
Допустим, что данная популяция животных характеризуется определенным распределением генотипов и разной частотой встречаемости тех или иных признаков. Задан характер скрещивания в популяции и относительная жизнеспособность носителей этих признаков при тех или иных условиях. Требуется найти, как изменится в последующих поколениях распределение признаков при существовании популяции в данной (неизменной или меняющейся по определенному закону) среде. Простейший случай такой эволюционной задачи – вопрос о том, с какой скоростью будет происходить вытеснение некоторого исходного гена его аллелем, возникшим в результате мутации и имеющим селекционное преимущество. Основными факторами, влияющими на этот процесс, является частота мутирования и эффективность отбора.
Пусть в случайно скрещивающейся популяции присутствуют два аллельных гена А и а, причем А доминантен, а вероятности того, что из оплодотворенного яйца со временем вырастут половозрелые особи, равны S для АА и Аа, для аа – S(1 – k).
Таким образом, если k положительно, то приспособленность аа ниже приспособленности АА и Аа. Предполагается, что плодовитости всех трех генотипов одинаковы. Как будет изменяться такая популяция и сколь быстро будут происходить эти изменения? Предположим для простоты, что поколения не перекрываются. В таком случае нам нужно выразить частоту аллеля в данном поколении через его частоту в предыдущем поколении (на той же стадии жизненного цикла).
Пусть частота аллеля А у взрослых особей в n-м поколении равна рn. При случайном скрещивании частоты зигот в следующем (n + 1)-м поколении будут pn2AA : 2pn(1 – pn)Aa : (1 – pn)2aa, а относительные частоты взрослых особей в (n + 1)-м поколении Spn2AA : 2Spn(1 – pn)Aa : S(1 – pn)2(1 –k)aa.
Теперь можно вычислить рn+1 – частоту аллеля А у взрослых особей в (n + 1)-м поколении как долю аллеля А в популяции с относительными частотами генотипов. Однако выражение, определяющее рn+1 через рn, получается довольно громоздким. Формула будет более компактной, если оперировать с величиной un = pn / (1 – pn), т. е. с отношением частоты аллелей А к частоте аллелей а. Тогда, поделив каждый член на (1 – рn)2, мы получаем относительные частоты генотипов в популяции взрослых особей в (n + 1)-м поколении в виде Sun2AA : 2SunAa :S(1 – k)aa, откуда un+1 = un(un + 1) : un + 1 – k.
Получено рекуррентное уравнение, позволяющее вычислять частоту аллеля А в (n + 1)-м поколении через его частоту в n-м поколении. Зная начальную частоту гена А и «коэффициент отбора» k против гомозигот аа, мы можем рассчитать частоту аллелей А и а в любом поколении. Так, при 1%-ном отборе частота первоначально редкого доминантного аллеля возрастает от 0,1 до 10% за 482 поколения, от 10 до 90% – за 1329 поколений, а для изменения частоты от 90 до 99,9% требуется почти 100 000 поколений. Столь длительное время, необходимое для полной элиминации рецессивного аллеля, объясняется тем, что редко встречающийся рецессивный аллель почти всегда находится в гетерозиготном состоянии и, следовательно, не подвергается отбору; по этой же причине частота выгодных, но редких рецессивных аллелей увеличивается очень медленно.
Математические модели в экологии
Объектом экологии служат сообщества разных видов животных и растений вместе с той физико-географической обстановкой, в которой они живут. Основная задача, возникающая перед исследователем в этой области – предсказание динамики численности видов, образующих биоценоз.
Достаточно сложная экологическая система, содержащая много видов, естественно оказывается системой с большим числом параметров.
При любой попытке описать эту систему математически многие существенные факторы неизбежно остаются вне сферы нашего внимания. И тем не менее такие попытки важны по двум причинам: во-первых, они намечают наиболее прямой путь к пониманию того, как влияют на поведение популяции взаимоотношения типа «хищник – жертва», «паразит – хозяин», территориальность, продолжительность периода до достижения зрелости и т. п.; во-вторых, они указывают, что именно следует измерять для того, чтобы можно было понять поведение какого-либо конкретного вида.
Представим себе животных, размножающихся один раз в год, например летом, и
погибающих до наступления следующего сезона размножения.
Пусть Х1, Х2, Х3, ..., Хn– численности взрослых самок в начале сезона размножения 1-го, 2-го, 3-го, … , n-гогода. Пусть из потомства каждой самки в среднем R самок доживает до сезона размножения следующего года. Тогда Xn+1 = RXn.
Это – рекуррентное соотношение, с помощью которого, зная численность популяции в данный момент, мы можем определить ее численность в будущем году.
Это соотношение можно записать и по-другому, так, чтобы оно описывало изменение численности популяции за год, т. е. Δ Хn = Xn+1 – Хn, и тогда, очевидно, ΔXn = (R – 1)Xn.
Величина R будет зависить от X, так например, если популяция велика, то ей для дальнейшего роста может не хватить пищи, и R будет мало. Но сначала мы рассмотрим случай, когда R постоянно. Итак, нам нужно решить уравнение Xn+ 1= RXn
При этом под «решением» уравнения мы понимаем определение X как функции номера поколения при «начальных условиях», в данном случае – Х1, т. е. численности популяции в первом поколении. Процесс решения рекуррентного уравнения обычно состоит из угадывания результата и доказательства того, что ответ угадан правильно, и в этом отношении напоминает интегрирование.
В данном случае легко догадаться, что решение имеет вид Xn = аλn , где а и λ – неизвестные постоянные.
Подставляя это выражение в уравнение, получим аλn+1=R аλnили λ = R. Откуда Хп= aRn.
Определим а из начальных условий: X1 = aR, или a = X1/R.
Таким образом, решение найдено: Xn = Х1/R Rn, или Xn=X1Rn-1
Рассмотренная выше зависимость определяется в математике показательной функцией, графиком которой является экспонента.
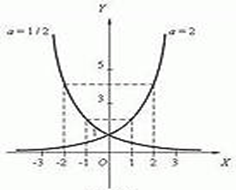
С помощью графиков данных функций наглядно можно показать в каком случае численность популяции будет увеличиваться, а в каком случае популяция будет идти к самоуничтожению.
Приведем пример, когда зная исходную численность популяции, скорость размножения R и число поколений, мы можем определить численность популяции в данном поколении.
Так, например, если n = 4, Х1= 1и R = 2, то X = 1 ∙23 = 8.
Покажем это на конкретной математической модели.
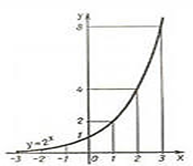
Построение соответствующей математической теории может дать ответ на ряд практически важных вопросов: прогнозирование численности промысловых животных и вредителей сельского хозяйства, допустимые нормы отлова и отстрела, вопросы оптимального использования природных ресурсов и охраны природы и др.
Взаимодействие и взаимопроникновение математики и предметов естественного цикла отвечает требованиям современной науки, делает все перечисленные предметы менее формальными, подтверждает факт достаточно искусственной их дифференциации. Обучение, построенное на принципах межпредметных связей, позволяет сформировать у учащихся объективную научную картину мира.
Таким образом, межпредметность – это современный принцип обучения, который влияет на отбор и структуру учебного материала целого ряда предметов, усиливая системность знаний учащихся, активизирует методы обучения, ориентирует на применение комплексных форм организации обучения, обеспечивая единство учебно-воспитательного процесса. Дальнейшее улучшение системы многосторонних межпредметных связей предполагает и дальнейшее совершенствование путей их реализации:
– учет межпредметных связей при планировании работы в школе;
– координацию деятельности всех участников педагогического процесса;
– эффективное использование межпредметных (комплексных) семинаров, экскурсий, конференций, на которых могут решаться проблемы средствами различных учебных предметов и наук одновременно.
учитель математики, заместитель директора по УВР МОАУ «Лицей № 21», г. Киров
Липатникова Валентина Александровна,
учитель биологии МОАУ «Лицей № 21», г. Киров
Аннотация. Статья посвящена вопросам установления межпредметных связей между некоторыми темами, изучаемыми в школьных курсах математики, химии, биологии и экологии. В ней описываются отдельный математические модели, применяемые в естествознании. Приводятся отдельные примеры.
Ключевые слова: обучение математике, обучение естествознанию, математика в классах химико-биологического профиля, межпредметные связи.
Анализ современных программ и учебников позволяет сказать, что во многих из них в должной мере не реализована идея межпредметных связей, которая необходима для формирования системных знаний учащихся. Следует особо отметить, что с накоплением знаний и дифференциацией наук будет увеличиваться опасность изучения предметов вне их естественной взаимосвязи. Чтобы ликвидировать разрыв между отдельными учебными дисциплинами, нужно определить такое обучение, при котором предметы дополняли бы друг друга, опирались бы один на другой с целью успешного изучения и проведения анализа изучаемых событий, явлений и законов на основе современных достижений науки. В конечном итоге такое обучение поможет выработать у учащихся умения и навыки рассматривать изучаемые явления во взаимозависимости и взаимосвязи.
Вышеизложенное и составило основу реализации идеи межпредметных связей математики, химии и биологии.
Установление межпредметных связей на уроках математики
Для того, чтобы возникла математика как наука, человек в течение многих веков изучал окружающую действительность, устанавливал связи, закономерности и лишь тогда формулировал законы, которым подчиняется живая и неживая природа, а затем развитие математики позволило решать задачи из разных областей знаний с помощью построения их математических моделей. Вот такой двухсторонний процесс следует показывать учащимся при изучении математики.
Особенно благоприятно такое обучение математике в классах химико-биологического профиля. Красота форм, встречающаяся в природе, привлекает человека и, говоря словами немецкого биолога Э. Геккеля, «природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные человеком формы». Существа, рассмотренные в книге Э. Геккеля «Красота форм в природе» красивы и симметричны, рассмотрение их на уроках математики при изучении тем «Симметрия» и «Золотое сечение» является целесообразным.
Формы и явления, встречающиеся в живой и неживой природе, не случайны. Одноклеточный организм феодария точно передает форму икосаэдра. Это объясняется тем, что из всех многогранников с таким же количеством граней именно икосаэдр имеет наибольший объем и наименьшую площадь. Это геометрическое свойство помогает морскому микроорганизму преодолевать давление водной толщи. Использование золотой пропорции помогло природе приспособить организмы к выживанию во внешней среде и оптимизировать их работу. Для оптимального использования воска пчела строит соты в форме правильной шестиугольной призмы.
Рассмотрение примеров рационального использования природой своих ресурсов является хорошей мотивацией к обучению математике учащихся химико-биологических классов, в частности к решению задач на отыскание наибольших и наименьших значений величин с помощью свойств производной.
Как располагать своими средствами для получения наибольшей выгоды – это важная задача для всей практической деятельности человека. С такими задачами приходится иметь дело представителям самых разных специальностей, в том числе и химикам.
Для того, чтобы учащимся показать, как применяются математические методы в химии, можно предложить решить следующую задачу.
Задача. В каком из хлорпроизводных предельных углеводородов процент (массовая доля) хлора максимальный?
Решение. Пусть k – количество атомов хлора (Cl), CnH2n+2 – общая формула предельных углеводородов. Уравнение: CnH2n+2 + kCl2 = CnH2n+2 = CnH2n+2–kClk + kHCl, где 1 ≤ k ≤ 2n+ 2, n > 0, n – натуральное. M(CnH2n+2–kClk) = M(Cl)∙k + M(C)∙n + M(H)∙(2n – 2 + k) – молярная масса вещества. ω(Cl) = (M(Cl)∙k) : M(Cl)∙k + M(C)∙n + M(H)∙(2n – 2 + k) – формула массовой доли. Подставив значения в формулу, получим: ω(Cl) = 35,5k : (12n + 2n + 2 – k + 35,5k). Рассмотрим функцию y(k) = 35,5k : (14n + 2 + 34,5k). Найдём её производную: y’(k) = (497n + 71) : (34,5k + 14n + 2)2. Так как n - натуральное, то производная всегда положительна, а значит, функция возрастает на всей своей области определения, в том числе на промежутке [1; 2n + 2], следовательно при значении k = 2n + 2 значение функции будет максимальным. Подставим 2n + 2 в исходную формулу CnH2n+2–kClk, получим CnCl2n+2, при наименьшем n = 1, получаем: хлорпроизводным предельным углеводородом с максимальным содержанием хлора является вещество CCl4 (его массовая доля ω(Cl) = 92,2%, а в следующем представителе C2Cl6 массовая доля хлора ω(Cl) = 89,9%).
Ответ. Хлорпроизводным предельным углеводородом с максимальным содержанием Cl является вещество CCl4.
Учащиеся химико-биологических классов без труда справляются с данной задачей.
Вещество CCl4 называется тетрахлорметан, модель его молекулы представляет собой правильный тетраэдр – это еще один повод вернуться к связям между математикой и химией.
Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли (NaCl), монокристалл алюмокалиевых квасцов KAl(SO4)2∙12Н2О имеет форму октаэдра, кристалл сернистого колчедана FeS имеет форму додекаэдра, сурьмянистый сернокислый натрий – тетраэдра, бор – икосаэдра. Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ.
Перечисленные выше и другие факты позволяют установить зависимость свойств химических веществ от числа симметрий правильных многогранников, составляющих их макроструктуры.
Соответствие макроструктур химических веществ правильным многогранникам
|
Название многогранника
|
Тетраэдр
|
Гексаэдр
|
Октаэдр
|
|
Общее число симметрий (осевая, центральная, зеркальная)
|
9
|
20
|
20
|
|
Химические вещества
|
Серная кислота, вода, метан, аммиак | Железо, медь, вольфрам, кремний | Углерод (алмаз) |
Таким образом, можно сделать вывод: чем более высокой симметрией обладают макроструктуры веществ, тем эти вещества прочнее, более блестящие, тем выше у них температуры кипения и плавления, лучше теплопроводность.
Установление межпредметных связей на уроках биологии
В современной биологии активно используются различные разделы математики: теория вероятностей и статистика, теория дифференциальных уравнений, теория игр, дифференциальная геометрия и теория множеств для формализации представлений о структуре и принципах функционирования живых объектов.
Многие ученые высказывали мысль о том, что область знаний становится наукой только тогда, когда выражает свои законы в виде математических соотношений. В биологии, для которой предметом изучения являются индивидуальные живые системы, дело обстоит сложнее. Только в ХХ веке появились экспериментальные биохимия, биофизика, молекулярная биология, микробиология, вирусология, которые изучают воспроизводимые явления и активно используют физические, химические и математические методы.
В связи с индивидуальностью биологических явлений говорят именно о математических моделях в биологии (а не просто о математическом языке).
Математические модели в генетике популяций и в теории эволюции
Эволюционный процесс можно рассматривать как процесс видового обучения или как процесс поиска оптимального состояния. При этом популяция выступает как регулируемая многопараметрическая система. Кроме того, эволюция может рассматриваться и как процесс группового поведения автоматов. С этой точки зрения, популяция – это совокупность «автоматов» (организмов), которые, взаимодействуя между собой и с внешней средой, решают свои собственные локальные задачи. Однако в результате такого взаимодействия система в целом решает некоторую интегральную задачу, например, приспособления вида к новой среде обитания. Ясно, что в данном случае речь идет о примере управления за счет локальных взаимодействий, так как у популяции нет централизованного управляющего механизма.
Допустим, что данная популяция животных характеризуется определенным распределением генотипов и разной частотой встречаемости тех или иных признаков. Задан характер скрещивания в популяции и относительная жизнеспособность носителей этих признаков при тех или иных условиях. Требуется найти, как изменится в последующих поколениях распределение признаков при существовании популяции в данной (неизменной или меняющейся по определенному закону) среде. Простейший случай такой эволюционной задачи – вопрос о том, с какой скоростью будет происходить вытеснение некоторого исходного гена его аллелем, возникшим в результате мутации и имеющим селекционное преимущество. Основными факторами, влияющими на этот процесс, является частота мутирования и эффективность отбора.
Пусть в случайно скрещивающейся популяции присутствуют два аллельных гена А и а, причем А доминантен, а вероятности того, что из оплодотворенного яйца со временем вырастут половозрелые особи, равны S для АА и Аа, для аа – S(1 – k).
Таким образом, если k положительно, то приспособленность аа ниже приспособленности АА и Аа. Предполагается, что плодовитости всех трех генотипов одинаковы. Как будет изменяться такая популяция и сколь быстро будут происходить эти изменения? Предположим для простоты, что поколения не перекрываются. В таком случае нам нужно выразить частоту аллеля в данном поколении через его частоту в предыдущем поколении (на той же стадии жизненного цикла).
Пусть частота аллеля А у взрослых особей в n-м поколении равна рn. При случайном скрещивании частоты зигот в следующем (n + 1)-м поколении будут pn2AA : 2pn(1 – pn)Aa : (1 – pn)2aa, а относительные частоты взрослых особей в (n + 1)-м поколении Spn2AA : 2Spn(1 – pn)Aa : S(1 – pn)2(1 –k)aa.
Теперь можно вычислить рn+1 – частоту аллеля А у взрослых особей в (n + 1)-м поколении как долю аллеля А в популяции с относительными частотами генотипов. Однако выражение, определяющее рn+1 через рn, получается довольно громоздким. Формула будет более компактной, если оперировать с величиной un = pn / (1 – pn), т. е. с отношением частоты аллелей А к частоте аллелей а. Тогда, поделив каждый член на (1 – рn)2, мы получаем относительные частоты генотипов в популяции взрослых особей в (n + 1)-м поколении в виде Sun2AA : 2SunAa :S(1 – k)aa, откуда un+1 = un(un + 1) : un + 1 – k.
Получено рекуррентное уравнение, позволяющее вычислять частоту аллеля А в (n + 1)-м поколении через его частоту в n-м поколении. Зная начальную частоту гена А и «коэффициент отбора» k против гомозигот аа, мы можем рассчитать частоту аллелей А и а в любом поколении. Так, при 1%-ном отборе частота первоначально редкого доминантного аллеля возрастает от 0,1 до 10% за 482 поколения, от 10 до 90% – за 1329 поколений, а для изменения частоты от 90 до 99,9% требуется почти 100 000 поколений. Столь длительное время, необходимое для полной элиминации рецессивного аллеля, объясняется тем, что редко встречающийся рецессивный аллель почти всегда находится в гетерозиготном состоянии и, следовательно, не подвергается отбору; по этой же причине частота выгодных, но редких рецессивных аллелей увеличивается очень медленно.
Математические модели в экологии
Объектом экологии служат сообщества разных видов животных и растений вместе с той физико-географической обстановкой, в которой они живут. Основная задача, возникающая перед исследователем в этой области – предсказание динамики численности видов, образующих биоценоз.
Достаточно сложная экологическая система, содержащая много видов, естественно оказывается системой с большим числом параметров.
При любой попытке описать эту систему математически многие существенные факторы неизбежно остаются вне сферы нашего внимания. И тем не менее такие попытки важны по двум причинам: во-первых, они намечают наиболее прямой путь к пониманию того, как влияют на поведение популяции взаимоотношения типа «хищник – жертва», «паразит – хозяин», территориальность, продолжительность периода до достижения зрелости и т. п.; во-вторых, они указывают, что именно следует измерять для того, чтобы можно было понять поведение какого-либо конкретного вида.
Представим себе животных, размножающихся один раз в год, например летом, и
погибающих до наступления следующего сезона размножения.
Пусть Х1, Х2, Х3, ..., Хn– численности взрослых самок в начале сезона размножения 1-го, 2-го, 3-го, … , n-гогода. Пусть из потомства каждой самки в среднем R самок доживает до сезона размножения следующего года. Тогда Xn+1 = RXn.
Это – рекуррентное соотношение, с помощью которого, зная численность популяции в данный момент, мы можем определить ее численность в будущем году.
Это соотношение можно записать и по-другому, так, чтобы оно описывало изменение численности популяции за год, т. е. Δ Хn = Xn+1 – Хn, и тогда, очевидно, ΔXn = (R – 1)Xn.
Величина R будет зависить от X, так например, если популяция велика, то ей для дальнейшего роста может не хватить пищи, и R будет мало. Но сначала мы рассмотрим случай, когда R постоянно. Итак, нам нужно решить уравнение Xn+ 1= RXn
При этом под «решением» уравнения мы понимаем определение X как функции номера поколения при «начальных условиях», в данном случае – Х1, т. е. численности популяции в первом поколении. Процесс решения рекуррентного уравнения обычно состоит из угадывания результата и доказательства того, что ответ угадан правильно, и в этом отношении напоминает интегрирование.
В данном случае легко догадаться, что решение имеет вид Xn = аλn , где а и λ – неизвестные постоянные.
Подставляя это выражение в уравнение, получим аλn+1=R аλnили λ = R. Откуда Хп= aRn.
Определим а из начальных условий: X1 = aR, или a = X1/R.
Таким образом, решение найдено: Xn = Х1/R Rn, или Xn=X1Rn-1
Рассмотренная выше зависимость определяется в математике показательной функцией, графиком которой является экспонента.

С помощью графиков данных функций наглядно можно показать в каком случае численность популяции будет увеличиваться, а в каком случае популяция будет идти к самоуничтожению.
Приведем пример, когда зная исходную численность популяции, скорость размножения R и число поколений, мы можем определить численность популяции в данном поколении.
Так, например, если n = 4, Х1= 1и R = 2, то X = 1 ∙23 = 8.
Покажем это на конкретной математической модели.

Построение соответствующей математической теории может дать ответ на ряд практически важных вопросов: прогнозирование численности промысловых животных и вредителей сельского хозяйства, допустимые нормы отлова и отстрела, вопросы оптимального использования природных ресурсов и охраны природы и др.
Взаимодействие и взаимопроникновение математики и предметов естественного цикла отвечает требованиям современной науки, делает все перечисленные предметы менее формальными, подтверждает факт достаточно искусственной их дифференциации. Обучение, построенное на принципах межпредметных связей, позволяет сформировать у учащихся объективную научную картину мира.
Таким образом, межпредметность – это современный принцип обучения, который влияет на отбор и структуру учебного материала целого ряда предметов, усиливая системность знаний учащихся, активизирует методы обучения, ориентирует на применение комплексных форм организации обучения, обеспечивая единство учебно-воспитательного процесса. Дальнейшее улучшение системы многосторонних межпредметных связей предполагает и дальнейшее совершенствование путей их реализации:
– учет межпредметных связей при планировании работы в школе;
– координацию деятельности всех участников педагогического процесса;
– эффективное использование межпредметных (комплексных) семинаров, экскурсий, конференций, на которых могут решаться проблемы средствами различных учебных предметов и наук одновременно.

 Е.
И. Шехирева
Е.
И. Шехирева