Некоторые классические диофантовы уравнения

Аннотация: В работе предпринята  попытка найти общие полные решения некоторых диофантовых уравнений второй степени с тремя переменными, проследить некоторые закономерности, предложить  общие  подходы, которые будучи элементарными,  тем  не  менее,  приводят к решению подобных уравнений. Использование арифметических функций позволило записать найденные решения в виде единой формулы без ограничений на используемые параметры.

Ключевые слова: диофантово уравнение, уравнения второй степени от трёх переменных.

 Работа  посвящена  одному  из  центральных  разделов  теории чисел – теории  диофантовых  уравнений.  

В прошлом году мы работали с  уравнением  Пифагора:  а² + b² = с², где а, b, с – натуральные числа,  имеющее бесконечное множество решений.  Работа была построена на отыскании общей формулы для задания всех решений уравнения Пифагора.  Дело в том, что в источниках, изученных нами, нет единой  формулы  для  задания  всех решений. Известные решения состояли из  объединения двух формул. Исключением оказалась аннотация работы  казахстанского  учёного Кожегельдинова С. Ш. [1],  который предложил одну общую формулу,  задающую все решения уравнения  Пифагора на основе использования арифметических функций.  В своей работе мы самостоятельно нашли способы вывода такой формулы, показали при каких параметрах из выведенной нами формулы можно получить решения, предлагавшиеся другими авторами [2] – [4], применили полученные знания к решению уравнения Пифагора в числах, обратных натуральным, рассмотрели перспективы дальнейшей работы над отысканием решений диофантовых уравнений.

В  рамках рассмотренных перспектив и была построена наша нынешняя работа.

Новизна данной работы состоит в применении арифметических функций при решении рассматриваемых задач, что позволяет записать одну общую формулу решений, вместо объединения нескольких формул, предлагаемых в известной литературе, при этом, выбранные параметры не имеют ограничений (например, по чётности).

Решение неопределённых уравнений имеет не только теоретический интерес. К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величины могут быть только целыми числами. Например, космические, астрономические задачи, задачи арифметической геометрии. Связь между данным вопросом теории чисел и свойствами правильных точечных решёток позволила развить и методы изучения последних, сыгравших чрезвычайно важную роль в решении ряда основных задач кристаллографии. Непосредственно задачи кристаллографии, а именно описание кристаллических решёток с помощью целочисленных уравнений, которые задают положение атомов в структуре кристаллической решетки, и послужило отправным пунктом для написания этой работы.

Имеется практическая необходимость выработать стандартный способ нахождения всех решений диофантовых уравнений  второй  степени  и  выше с  двумя  и  более  переменными,  но на сегодняшний день, не существует единого способа или приёма,  позволяющего решить  любое диофантово уравнение,  если его степень  выше  первой. 

            Указанное  противоречие  позволило сформулировать цель и задачи нашей работы, исходя из уровня личных знаний.

Нахождение способа задания общей  формулы всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными на множестве натуральных чисел.

Если  удастся  найти способ задания общей  формулы для нахождения  всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными, то возможно удастся  применить полученные  результаты и для решения других задач  данного  раздела  математики, а может быть и для диофантовых уравнений определённых видов второй  и  выше степени с двумя и более переменными, так как многие проблемы математики решались для частных случаев, а после обобщались.

Объект исследования: некоторые диофантовы уравнения  второй  степени  с  тремя  переменными.

Предмет исследования: процесс нахождения общего решения некоторых неопределённых уравнений второй  степени  с  тремя  переменными на множестве натуральных чисел.

Задачи:
1. Познакомиться с методами и приёмами, использовавшимися для решения уравнения Пифагора и задач, связанных с ним.
2. Рассмотреть возможность использования арифметических функций к решению близких  диофантовых уравнений.
3. Самостоятельно вывести общую формулу некоторых диофантовых уравнений  второй  степени  с  тремя  переменными.
4. В случае удачи, рассмотреть возможность применения полученных результатов к решению более общих задач неопределённого анализа.   

Планирование  ожидаемых  результатов:

Работа над проектом поможет найти общую формулу решений некоторых диофантовых уравнений  второй  степени  с  тремя  переменными и оценить перспективы применения полученных результатов для решения других  неопределённых  уравнений второй степени.

Полученные результаты могут быть использованы в кристаллографии. Например, при изучении пространственной изомерии, структур решёток веществ, имеющих плоское или плоско-сетчатое строение, как, например, графит.

Критерии  оценки  ожидаемых  результатов:
- выявление возможности использования арифметических  функций к решению некоторых диофантовых уравнений второй степени с тремя неизвестными на множестве натуральных чисел;
- нахождение единой формулы всех решений некоторых диофантовых уравнений  второй  степени  с  тремя  переменными;
-  рассмотрение возможности использования полученных результатов для решения близких задач.       

При  k = 1 из  формулы  (8)  получается  формула  (7). Положив в формуле (8) а  и  в  конкретными числами найдём частные  решения  уравнения (1).  Например,   при   k = 1 

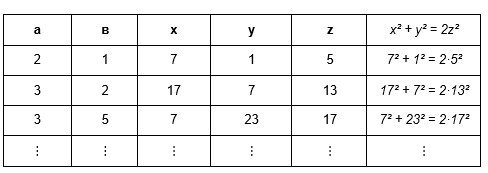
является  квадратом  некоторого  числа,  другое –  удвоенным  квадратом того же или  другого  числа.  Иначе  говоря,  если  первое число  является  квадратом  некоторого числа,  то  второе – удвоенным квадратом того же  или  другого  числа  и  наоборот,  если второе  число  является  квадратом  некоторого  числа,  то  первое – удвоенным  квадратом  того же  или  другого  числа.  При  этом  нетрудно  доказать,  что если числа  m и  n взаимно простые,  то  и  числа  (_*)  будут  взаимно  простыми. § 2.2    Решить  уравнение   х² + 2у²  =  z²    (9) где  x, y, zϵ N.
Прежде чем переходить к решению уравнения (9) заметим, что для  любых  чисел   m,  n ϵ N   одно  из  двух  чисел

В  самом  деле,  пусть  (m, n) = 1.  Тогда,  если: 

1)     m – нечётно, то  при  любой чётности  n  число (2, m) = 1  и, следовательно,

2)  m – чётно  (следовательно, n – нечётно), то при   (2, m) = 2.  Пусть  m = 2k,  где  k ϵ N. Поэтому  будем  иметь, что

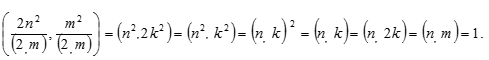
Таким  образом,  в  обоих  случаях  получаем,  что  числа  (_*) взаимно  простые,  если   (m, n) = 1.

  Очевидно,  что  если  ‹a, b, c› – решение  (26), то и  любая  тройка ‹ka, kb, kc›, где  k ϵ N, также является решением (26). Поэтому  достаточно  найти общую формулу  всех  основных  троек, то есть таких, для которых (х, у, z) = 1.  Для  отыскания  такой  формулы  будем  рассматривать не  уравнение (26), а равносильное  ему  уравнение

2y² = (z + x)(z – х),    (10)

где  x, y, zϵ N,  z– x ˃ 0.  Так  как  левая  часть  уравнения (10)  делится  на  2,  то  и правая часть должна  быть  чётной.  Если  

Положив в формуле (14) k= 1 получим формулу (13), которая является общей формулой всех основных троек. Подставив в формулу (14) конкретные числаmи nмы получим частные решения уравнения (9). Например, при k= 1 имеем

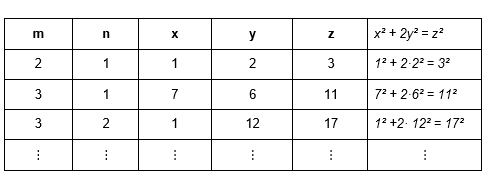
Легко показать, что если в уравнении (12) положить

§ 2.3 Рассмотрим более сложное уравнение

                                           х² + ру² = z²                                                                 (16)

где р, x, y, zϵ N,р – простое число.

 При решении этого равнения будем пользоваться обозначениями и результатами, полученными в предыдущих пунктах.

Если р|х, то обозначив х = рх₁, можно переписать уравнение (16) как р² х₁² + ру² = z². Откуда следует, что р|z; положив z = рz₁ имеем рх₁² + у² = рz₁². Следовательно, р|у, но тогда (х, у, z) = р≠1 в общем случае. Однако, очевидно, что если ‹х, у, z› – решение уравнения (16), то и ‹kх, kу, kz›, где k ϵ N, также является решением уравнения (16), а, значит, для решения данного уравнения нам достаточно найти основные тройки, то есть такие, для которых (х, у, z) = 1. Следовательно предположение о том, что р|х неприемлемо. Таким образом, потребуем, чтобы выполнялось условие (х, ру) = 1. Аналогично, (х, рz) = 1.

Перепишем уравнение (16) следующим образом

рy² = (z + x)(z – х),                                                                     (17)

Если z и х – разной чётности, то либо

a)         z + х = рu,       z – х = v,

либо

b) z + х = u,                 z – х = рv,

где u, v ϵ N, z – x ˃ 0.

Рассмотрим случай а). В этом случае положим

где р, m, nϵ N, (m, n) = 1, рn² > m², m, n – разной чётности,которая является общей формулой всех основных решений уравнения (19).

Формула (23) обращается в формулу (21), если (р, m) = 1 и в формулу (22), если (р, m) = р. Других вариантов быть не может, так как р – простое число.

Формулы (20) и (23), в свою очередь, так же можно объединить в единую формулу,

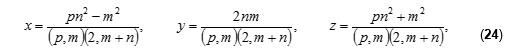
где р, m, nϵ N, (m, n) = 1, рn² > m², которая является общей формулой всех основных троек и не содержит более ограничений чётности на числа mи n. Очевидно, что если mи n – нечётны, то (2, m+n) = 2 и из формулы (24) получается формула (20), если же mи n – разной чётности, то (2, m+n) = 1 и формула (24) обращается в формулу (23). Других вариантов нет, поскольку (m, n) = 1.

 Теперь несложно написать и общую формулу всех троек

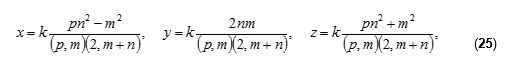
где k, р, m, nϵ N, (m, n) = 1, рn² > m.

Легко показать, что при р = 2 из формул (25) получаются формулы (14), являющиеся решениями уравнения (9), которое, в свою очередь, получается из уравнения (16) при р = 2.

Полагая в уравнении (16) р конкретным натуральным числом, получим частные уравнения, для которых при фиксированных натуральных чисел m и nможно найти частные решения. Например, положив р = 3 уравнение (16) примет вид: х² + 3у² = z²                                                                

При р = 5:  х² + 5у² = z²

где р, x, y, zϵ N. Варьируя параметры в формуле (25) получим частные решения уравнения (16). Несколько примеров при к = 1 содержит следующая таблица: 

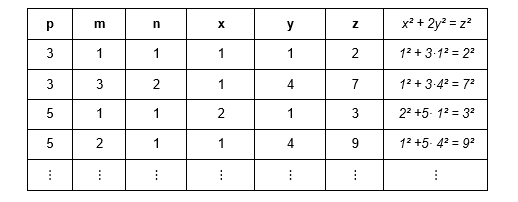
Исследуемое в работе противоречие не было устранено, однако мы смогли применить рассмотренные в предыдущей  работе приёмы для нахождения стандартных способов отыскания всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными.

Выводы

 Итак, в результате проведённого исследования были  найдены общие формулы решения некоторых диофантовых уравнений второй степени от трёх переменных. На основе полученных решений, можно сделать вывод, что  найденные подходы могут быть использованы к нахождению общих решений близких диофантовых уравнений. 

То есть, нашла подтверждение гипотеза о том, что если найти  способ задания общей  формулы для нахождения  всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными, то возможно удастся  применить полученные  результаты и для решения других задач  данного  раздела  математики.

Рассмотренные  объект и  предмет  исследования позволили достигнуть поставленной цели: на основе ранее полученных результатов были найдены способы задания общей  формулы всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными на множестве натуральных чисел.

 Обзор  литературы

Литература, в которой освещается проблема диофантовых уравнений, в том числе уравнение Пифагора, не многочисленна.   В изученной нами литературе рассмотрены некоторые способы нахождения решений уравнения Пифагора и уравнения х² + 2у² = z²   [2, 3, 4]. Приводятся общие формулы решения для указанных уравнений [1, 3].  Но в тех источниках, которыми  мы располагаем, не  приводятся  расчёты  подобные  сделанным  в  данной работе.  Так же нами показано как можно получить все классические формулы, из найденных нами  формул, варьируя параметры.  Мы не располагаем данными об освещении решений уравнений  х² + у²  = 2z²   и   х² + ру²  = z² , где р – простое число, а так же о том рассматривались ли они в каких-либо источниках.

Ссылки на источники:

1. Кожегельдинов С. Ш. О задачах, связанных с пифагоровыми тройками // Межвузовская конференция, посвящённая 150–летию со дня рождения Абая.  СГУ имени Шакарима,1991 г., стр. 132 – 133
2. Башмакова И. Г. Теория  чисел.  М.:  Наука, 1992 г.
3. Гельфонд А. О. Решение  уравнений  в  целых числах. М.: ИТКЛ, 1987г.
4. Литцман В. Теорема Пифагора и пифагоровы  тройки.  М.: Знание, 2008 г.