Внеклассное мероприятие по математике в 5- 6 классах «Тропа семи испытаний»

Аннотация. В статье представлено внеклассное мероприятие по математике в 5-6 классах, которое рассчитано на 2 часа. В содержании подобраны задачи по различным темам, изученным в 5-6 классах. Занятие проводится в форме игры- путешествия, для более успешного проведения которого рекомендуется использовать презентацию с картинками, анимацией, звуками.
Ключевые слова: занимательная математика, внеклассное мероприятие, игра- путешествие, дополнительное математическое образование. 

Внеклассное мероприятие — это организованный педагогом вид деятельности школьников во внеучебное время. 
Внеклассная деятельность способствует раскрытию индивидуальных способностей, творческого личностного потенциала ребенка, его умений и навыков, которые не всегда можно рассмотреть на уроке. Проведение внеклассных мероприятий в первую очередь направлено на удовлетворение интересов самих школьников, развитие способностей в различных сферах общения и деятельности, раскрытие творческого потенциала.
Мероприятия такого плана повышают интерес к предмету и способствуют осмыслению важной идеи: математика есть везде. В процессе изучения математики дети на основе решения задач различных типов учатся анализировать данные, выделять из них существенные и не существенные, разрабатывать алгоритм решения задач, а затем применять его на практике. Этот процесс развития мыслительной деятельности приводит к тому, что многие дети в дальнейшем могут самостоятельно решать сложные задачи. В данной статье предлагается разработка внеклассного мероприятия по математике в 5- 6 классах.

          Цель: способствование проявлению творческих умений,  познавательного интереса учащихся.

          Задачи:

• образовательные: учить в процессе реальной ситуации применять знания, умение работать с учебной информацией, повысить уровень математического развития;
• воспитательные: формировать интерес к математике, воспитывать чувство ответственности, коллективизма и взаимопомощи, аккуратность, точность и внимательность, культуру общения;
• развивающие:  в увлекательной игровой форме способствовать развитию познавательной активности учащихся, творческого потенциала, логического мышления, быстроты реакции, внимания, математического кругозора

Формы работы учащихся: групповая, парная, индивидуальная.

Используемые технологии: развивающее обучение,  игровая технология.

Необходимое оборудование: рисунки грибов, мяч, 2 набора карточек (цифры от 0 до 9), два набора карточек (числа от 1 до 20), карточки с числами (десятичные дроби, обыкновенные дроби, натуральные числа), раздаточный материал (тексты задач),  жетоны, маршрутные листы, наградной материал, оформление «остановок».

План мероприятия:

1. Построение участников игры – путешествия
2. Знакомство с правилами и критериями оценки
3. Вручение маршрутных листов
4. Игра – путешествие «Тропа семи испытаний»

• Харчевня «Три поросёнка»
• Тупик нечистой силы
• Заколдованный лес
• В некотором царстве, в некотором государстве …
• Волшебная лавка
• Город Мастеров
• В каморке у папы Карло

1. Построение участников игры-путешествия для подведения итогов.

Ход мероприятия:

• Харчевня «Три поросёнка»

             Меню:

1. Салаты: закуска грибная [1].
2. Первые блюда: суп из математических смекалок [2].
3. Вторые блюда: гарнир – кроссворд «И в шутку, и всерьёз» [3].

                                              Повара: три поросенка

Закуска грибная (в кабинете спрятаны нарисованные грибы, на которых записаны загадки с числами: надо найти грибы и отгадать загадки)

Где берёзки да дубы

Летом выросли  грибы.

Тут - волнушки и опята,

Там - лисички и маслята.

Под сосной - боровики,

Так им рады грибники (М. Абина)

Загадки:

-        Какое животное имеет два носа? (носорог: один – на теле, другой – в  названии);
-        Два брата купаются, а третий насмехается (два ведра и коромысло);
-        Двенадцать братьев друг за другом бродят, друг друга не обходят (двенадцать месяцев);
-        Есть семь братьев: годами равные, именами разные (дни недели);
-        Лежит брус на всю Русь. На том брусу 12 гнёзд. И во всяком гнезде по четыре птицы (год);
-        Только одно дерево без ветра шумит. Какое? (осина);
-        Шесть ног, а бежит не быстрее, чем на четырёх (всадник на коне);
-        Два раза родится, а один раз умирает (птица);
-        Сто один брат и все в один ряд, вместе связаны, стоят (изгородь);
-        Стучит, гремит, вертится, ничего не боится. Считает наш век, а не человек (часы);
-        На четырех ногах стою, ходить же вовсе не могу (стол, стул) 

Суп из математических смекалок

-       В харчевню пришли 11 человек и потребовали подать им по рыбине. К сожалению, у хозяина оказалось всего 3 небольшие рыбины. Тем не менее, хозяин не желал упустить случая, поживиться: имея в своем распоряжении три рыбы, он обещал гостям подать на стол 11. Гости заинтересовались этим и даже согласились уплатить деньги вперед. Как хозяин харчевни исполнил свое обещание?

(Положил рыбу на тарелку так: ХI)

-       На улице в 11 часов вечера идет дождь. Можно ли утверждать, что через 72 часа будет солнечная погода?

(Нет, так как будет ночь)

-       В корзине лежат четыре яблока. Можно ли эти яблоки поделить поровну между четырьмя братьями так, чтобы в корзине осталось одно яблоко? Резать яблоки не разрешается.

(Да, одному из них надо дать яблоко в корзине)

Гарнир – кроссворд «И в шутку, и всерьёз»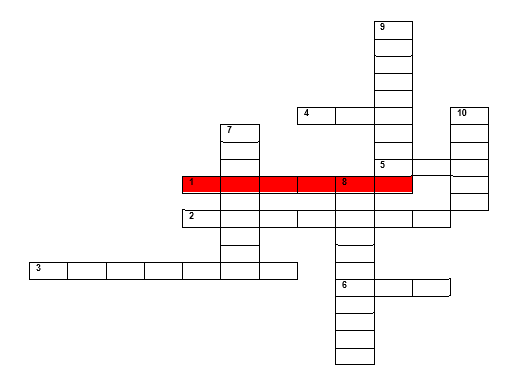

По горизонтали:

1. ?.

2. Арифметическое действие.

3. Ученый – математик.

4. Самая нелюбимая оценка ученика.

5. Прямоугольный параллелепипед, у которого все ребра равны.

6. Геометрическая фигура, которая дружит с солнцем.

По вертикали:

7. Равенство, содержащее переменную.

8. Проверка учеников на выживание.

9. Учебник, напичканный задачками.

10. Забор для математических действий

Ответ: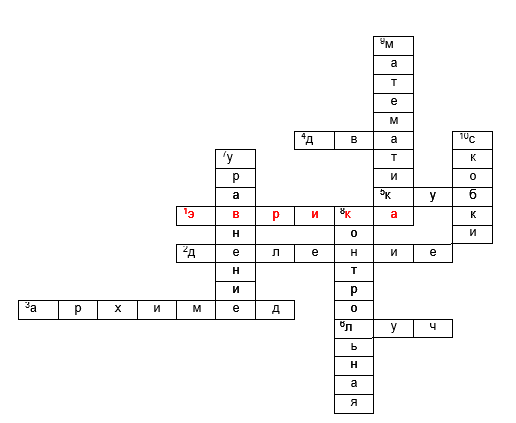

• Тупик нечистой силы   

Ребят встречают Баба Яга, Леший, Кикимора. Грозят дальше не пропустить, если не развлекут их. Предлагают поиграть с ними в игры.

    «Каждое число свое место любит»

У каждого играющего (любое количество) набор карточек, на которых написаны числа от 1 до 20. Ведущие перемешивают карточки. По сигналу участники начинают раскладывать их по порядку. Выигрывает тот, кто выполнит  задание первым.

    «Таблица умножения»

У каждого играющего (любое количество или команды) набор карточек, на которых написаны цифры (от 0 до 9). Ведущий называет  табличный случай умножения. Например, 9 ∙ 6. Балл зарабатывает тот участник, который первым покажет результат умножения. Игра проводится несколько раз. Выигрывает участник, набравший большее количество баллов.

          «Молекулы» [4]

Участники изображают движение молекул. По команде ведущего: «Молекула – 3» («Молекула – 5», «Молекула – 7» и т.д.) игроки разбиваются в группы по 3 (5, 7 и т.д.) человека. Тот, кто не сможет встать в тройки, выбывает из игры. По команде: «Молекула свободна» участники изображают свободное движение. Далее ведущий продолжает менять количество молекул. Игра продолжается до тех пор, пока не останется минимум игроков, которые и объявятся победителями.

Игру можно усложнить:

- молекулы двигаются с закрытыми глазами;

- проигравшие не покидают площадку, а просто стоят на месте. Получается, что они мешают играющим.

         «Не скажу»

Ученики по порядку называют числа. Вместо чисел, которые делятся на 3, говорят: «Не скажу». Тот, кто ошибается, выбывает из игры.

         «Собери числа»

В помещении, в котором проводится игра,  разбросаны  листочки с числами (десятичные дроби, обыкновенные дроби, натуральные числа).  Задание играющим (несколько человек или группы): по команде распределить числа. Один собирает только натуральные числа, другой – десятичные дроби и т.д.

«Назови число»

Играющие становятся в круг. Ведущий с мячом в руках внутри круга. Он бросаете мяч то одному, то другому участнику игры, а те возвращают его обратно. Бросая мяч, ведущий называете какое-либо число, например 25, играющий должен назвать смежные числа – 24 и 26. Можно поставить условие, что сначала должно быть названо меньшее число, а потом большее.

Игру можно усложнить. Возвращая мяч, играющий должен сначала отнять от названного вами числа единицу, а потом прибавить к нему разность. Например, вы назвали число 25. Играющий сначала отнимает от него единицу (25-1=24), потом прибавляет 24 (25+24=49) и называет число 49.

   «Третий лишний»

Игроки становятся по кругу парами друг за другом лицом к центру. Расстояние одной пары от другой 1 – 2 м. Назначаются двое водящих, которые занимают место за кругом. Один убегает, другой догоняет. Убегающий встает впереди любой пары, сзади стоящий в этой паре игрок (он оказывается «третьим лишним») быстро убегает. Если догоняющий осалит убегающего, то сам теперь убегает и может встать впереди любой пары. Никто не должен мешать игроку убегать от преследователя.

• Заколдованный лес

Старичок- лесовичок: «Так вышло, что именно вы оказались в заколдованном лесу. Чтобы вернуться домой, вам нужно с леса снять чары злой волшебницы. Для этого необходимо правильно ответить на вопросы математической викторины» [5].

Вопросы викторины:

ü  Какой знак нужно поставить между цифрами 3 и 4, чтобы получилось число больше, чем 3, но меньше, чем 4?

(плюс; запятую; деление)

ü  7 рыбаков съели 7 судаков за 7 дней. За сколько дней 10 рыбаков съедят 10 судаков?

(7 дней; 10 дней; 1 день)    

ü  Сколько трехзначных чисел можно записать с помощью цифр 1, 2, 3, при условии, что цифры не повторяются?

(3; 6; 5)    

ü  От какого слова происходит название цифры «Нуль»?

(мало; недостаточно; пусто)    

ü  Как правильно пишется слово «_д_ница»?

(еденица; идиница; единица)     Слайд 7

ü  Число, которое не относится ни к простым, ни к составным?

(3; 1; 2)    

ü  Кто автор первого русского учебника математики?

(Магницкий; Виленкин; Колмагоров)   

ü  Площадь квадрата равна 196 см². Чему равна длина стороны?

(49 см; 98 см; 14 см)    

ü  Числа, которые употребляются при счете предметов

(целые; рациональные; натуральные)   

• В некотором царстве, в некотором государстве …

Перед гостями появляется царевна Несмеяна со свитой. Царевна Несмеяна грустит, нянька причитает: «Всего много, все есть, чего душа хочет, а никогда она не улыбается, никогда не смеется, словно сердце ее ничему не радуется. Помогите, гости дорогие! Развеселите царевну нашу» (задание: спеть песни, частушки, в тексте которых встречаются числа).

• Волшебная лавка

Волшебник предлагает решить задачи разного уровня сложности [6]. Ребята, решив задачи, смогут получить 1 жетон, 3 жетона, 5 жетонов.  Уровень сложности выбирают сами. Решают либо по одному, либо группами, либо все вместе.

ü  5 класс

1 жетон

Задача №1. Три поросенка построили три домика: из соломы, из прутьев и из камней. Каждый из них получил один домик:  Ниф-Ниф – не из камей и не из прутьев; Нуф-Нуф – не из камней. Объясните, какой домик достался Наф-Нафу?

Ответ: Наф-Нафу достался домик из камней.

Задача №2. Илья Муромец, Добрыня Никитич, Алеша Попович вступили в бой с несколькими великанами. Получив по три удара богатырскими палицами, великаны обратились в бегство. Больше всего нанес ударов Илья Муромец: 7, меньше всего - Алеша Попович: 3. Сколько всего было великанов?

Ответ: 5 великанов.

Задача №3. Малыш может съесть 100 граммов варенья за 6 минут, а Карлсон – в два раза быстрее. За какое время они съедят это варенье вместе?

Ответ: 2 минуты

3 жетона

Задача №1. У щенят и утят вместе 44 ноги и 17 голов. Сколько щенят и сколько утят?

Ответ: 5 щенят и 12 утят.

Задача №2. Парусник отправляется в плавание в понедельник в полдень. Плавание будет продолжаться 100 часов. Назови день и час его возвращения в порт.

Решение. В сутках 24 часа, поэтому 100 ч = 4 ∙ 24 ч + 4 ч = 4 сут + 4 ч. Поэтому парусник вернется в пятницу в 16 ч.

Ответ: пятница, 16 ч.

Задача №3. Вычислите: 101101 ∙ 999 – 101 ∙ 999999.

Решение. 101101 ∙ 999 – 101 ∙ 999999 = 101 ∙ 1001 ∙ 999 – 101 ∙ 999 ∙ 1001 = 0.

Ответ: 0

5 жетонов

Задача №1. Даны числа от 1 до 9. Расставьте их в кружки так, чтобы сумма трех чисел вдоль каждой линии была равна 15. Какое число должно быть в центре?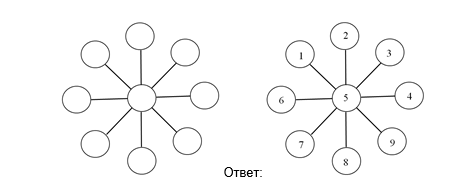

Задача №2. Как с помощью семилитрового ведра и трехлитровой банки налить в кастрюлю ровно 5 литров воды?

Решение. С помощью трехлитровой банки нальем 6 л воды в ведро.

Еще раз нальем 3 л воды в банку и наполним семилитровое ведро доверху. Тогда в банке останется 2 л воды, которую выльем в кастрюлю. Добавим к ним 3 л воды с помощью банки, получим всего 

5 л воды. Возможны и другие варианты решения.

Задача №3. Найдите сумму: 1 + 2 + 3 + … + 111.

Решение. Напишем искомую сумму дважды:

S = 1 + 2 + 3 + … + 109 + 110 + 111,

S =111 + 110 + 109 + … +3 + 2 + 1.

Сложим почленно:

2S = (1 + 111) + (2 + 110) + … + (110 + 2) + (111 + 1) = 112 ∙ 111.

Тогда S= 112 ∙ 111 : 2 = 6216.

Ответ: 6216.

6 класс

1 жетон

Задача №1. В записи 1*2*3*4*5 замените «*» знаками действий и расставьте скобки так, чтобы получилось выражение, значение которого равно 100.

Ответ: 1 ∙ (2 + 3) ∙ 4 ∙ 5 = 100.

Задача №2. Пришел Иван-царевич в подземелье к Кощею Бессмертному Василису Прекрасную освобождать. В подземелье три темницы. В одной из них томится Василиса, в другой расположился Змей Горыныч, а третья темница – пустая. На дверях есть надписи, но они все ложные. На первой темнице написано: «Здесь Василиса Прекрасная»; на второй темнице: «Темница №3 не пустая»; на третьей темнице написано: «Здесь Змей Горыныч». В какой же темнице Василиса?

Ответ: Василиса Прекрасная не может быть в первой темнице, значит она во второй или третьей. Так как темница 3 – пустая, то Василиса Прекрасная будет во второй темнице.

Задача №3. Даны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Расставьте их так, чтобы сумма их на каждой стороне треугольника была равна 20.

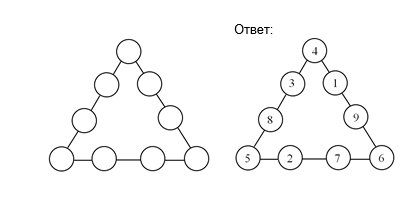
3 жетона

Задача №1. Лошадь может съесть воз сена за 1 месяц, коза – за 2 месяца, а овца – за три месяца. За какое время лошадь, коза и овца съедят такой же воз сена?

Решение. За один год лошадь съест 12 возов сена, коза – 6, а овца – 4 воза сена. Всего за год они вместе съедят 22 воза сена. Тогда один воз сена они съедят все вместе за 12 : 22 = 6/11 (месяца).

Ответ: 6/11 месяца.

Задача №2. Как, имея два сосуда вместимостью 5 л и 7 л, налить из водопроводного крана 6 л?

Решение. Наполняем семилитровый сосуд, переливаем из него 5 л в пятилитровый, затем 5 л выливаем, а оставшиеся 2 л в семилитровом сосуде выливаем вновь в пятилитровый сосуд.

Снова наполняем семилитровый сосуд, отливаем из него 3 л в пятилитровый сосуд. Тогда в семилитровом остается 4 л.

Выливаем все из пятилитрового сосуда и выливаем в него 4 л из семилитрового сосуда.

Наполняем вновь семилитровый сосуд, отливаем из него 1 л в пятилитровый сосуд. Таким образом, в семилитровом сосуде получаем 6 л.

Задача №3. На школьной викторине участникам предложили 20 вопросов. За правильный ответ ученику ставилось 12 очков, а за неправильный списывали 10 очков. Сколько правильных ответов дал один из учеников, если он ответил на все вопросы и набрал 86 очков.

Решение. Всего 20 вопросов. Пусть х ответов было правильных, тогда (20 – х) ответов неправильных.

12х – 10(20 – х) = 86,

х = 13

Ответ: 13 правильных ответов.

5 жетонов

Задача №1. Разместите восемь козлят и девять гусей в пяти хлевах так, чтобы в каждом хлеве были и козлята, и гуси, а число их ног равнялось 10.

Решение. Обозначим число гусей в одном хлеве за х, а число козлят за у. Тогда, учитывая, что ног в одном хлеве должно быть 10, получим уравнение: 2х + 4у = 10. Из данного уравнения имеем, что число козлят может быть только 1 или 2, соответственно гусей будет 3 или 1. Тогда размещение будет такое: в двух хлевах будет по одному козленку и 3 гуся, в трех хлевах – по 2 козленка и 1 гусю.

Задача №2. Школьник прочитал книгу за три дня. В первый день он прочитал 0,2 всей книги и еще 16 страниц, во второй день – 0,3 остатка и еще 20 страниц. В третий день – 0,75 остатка и последние 30 страниц книги. Сколько страниц в книге?

Решение. Пусть х – число страниц, которое было в книге. В первый день прочитали (0,2х + 16) страниц; осталось прочитать во второй и третий дни (0,8х – 16) страниц;

во второй день прочитали (0,3(0,8х – 16) +20) = (0,24х + 15,2) страниц; в третий день прочитать осталось (0,56х – 31,2) страниц. Так как в третий день прочитали 0,75 остатка и еще 30 книг, то остаток будет составлять 120 страниц. В итоге получаем уравнение 0,56х – 31,2 = 120. Откуда находим х = 270.

Ответ: 270 страниц.

Задача №3. Разделите семь яблок поровну на 12 человек, не разрезая яблоки более чем на 4 части.

Решение. Так как то надо разделить 3 яблока на 4 части, а 4 яблока каждое на 3 части и каждому человеку дать по  и  яблока.

• Город Мастеров

Гостей встречает Данила-мастер и предлагает заняться строительством.

(Работа с пазлами: необходимо за отведенный промежуток времени сложить как можно больше картин.)

• В каморке у папы Карло

Папа Карло встречает ребят, приглашает их заглянуть в его каморку: «Выполните задания, получите золотой ключик, откроете заветную дверцу, продолжите путешествие!» [7].

•  Из спичек построен дом. Переложите 2 спички так, чтобы дом повернулся другой стороной.    

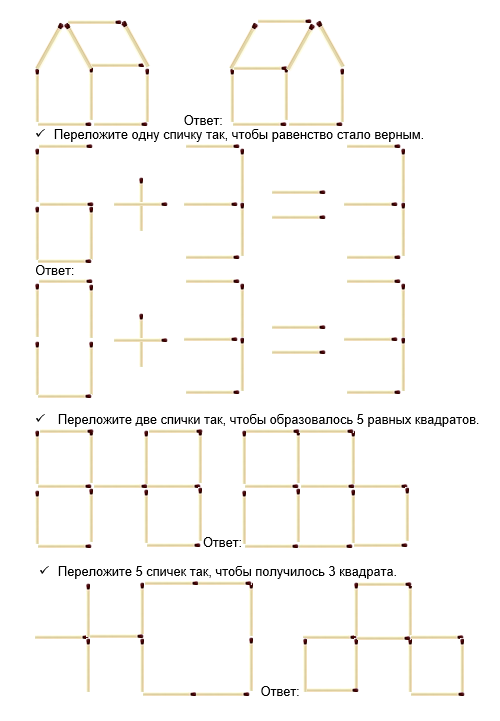
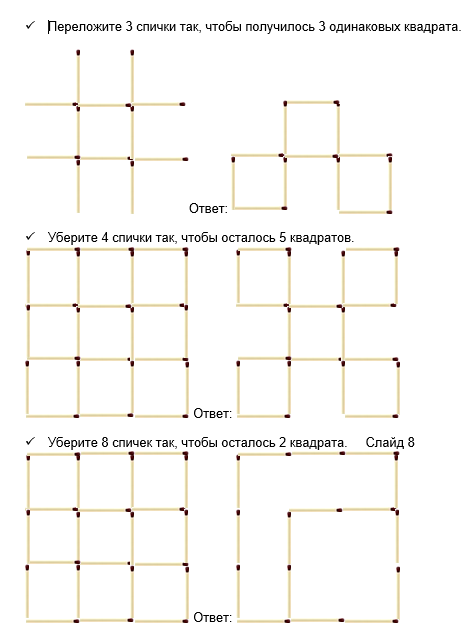
1. 1.    Построение участников игры – путешествия для подведения итогов 

Ссылки на источники:

1. Гельфан Е.М. «Арифметические игры и упражнения», М.: «Просвещение», 1988
2 . Приложение к газете «Первое сентября» «Математика»
3 . Шарыгин И.Ф., Шевкин А.В. «Математика. Задачи на смекалку», 5 – 6 классы, М.: «Просвещение», 1998
4 . Гельфан Е.М. «Арифметические игры и упражнения», М.: «Просвещение», 1988
5 . Приложение к газете «Первое сентября» «Математика»
6 . Фарков А.В. «Математические олимпиады в школе», 5 – 11 классы, М.: «Айрис – пресс», 2006
7 . Гельфан Е.М. «Арифметические игры и упражнения», М.: «Просвещение», 1988