Обучающая олимпиада – одна из форм внеурочных занятий математикой

Аннотация. В статье рассматривается методика проведения обучающей олимпиады по математике.  Автор на примере погружения в тему «Тайны графов» описывает схему проведения таких олимпиад, приводит тексты задач с решениями, которые могут быть использованы на том или ином этапе олимпиады, приводит конспект внеурочного занятия, построенного с использованием деятельностного подхода.
Ключевые слова: обучающая олимпиада, внеурочное занятие, граф, обход графа, вершины графа, задача. 

Как математику из «науки скучных цифр» превратить в «царицу наук»? Как помочь школьнику проявить себя «великим математиком» и заинтересовать его новыми открытиями? Именно участие в олимпиаде покажет ребятам, что каждая встреча с математикой – знакомство с волшебным и прекрасным миром. Участвуя в олимпиаде, ребята под руководством своих наставников не только смогут раскрыть себя, но и найдут ответы на разные вопросы, узнают много нового и интересного. Обучающая олимпиада как форма внеурочной работы играет огромную роль в развитии познавательного интереса учащихся, соревновательный мотив является для них подкреплением познавательному мотиву, способствует активности мыслительной деятельности, повышает концентрированность внимания, настойчивость, работоспособность, интерес, создает условия для появления радости успеха, удовлетворенности, чувства коллективизма.

В ходе олимпиады необходимо показать участникам практическую значимость и внутреннюю красоту математики как науки. Очень важно организовать профессиональный диалог педагогов для повышения их профессиональной квалификации.

Программа проведения обучающей олимпиады по математике.

Прежде всего необходимо определить временной промежуток в течение которого будет проходить обучающая олимпиада. Длительность проекта может быть различна: учебный год, одна четверть, один месяц или неделя.

Участники: математический кружок, класс, параллель, школа, несколько школ района и т.д.

Разбиваем олимпиаду на этапы.

Координаторы: сообщество учителей математики.

Первый этап - подготовительный. Регистрация участников. Конкурс визиток.

Второй этап– обучающий тур. Участники получают задания (/ответы). Команды работают над изучением теоретического материала и заданиями обучающего тура (формы каждая команда выбирает самостоятельно). Отчет о проведении обучающего тура каждая команда представляет в виде презентации, статьи, видеоролика.

Третий этап -блиц-конкурс. Команды предлагают друг другу задачи для решения, определяют наиболее интересные задачи, оценивают работу команд соперников.

Четвертый этап– конкурсный тур (очный этап олимпиады).

Завершающий этап - подведение итогов олимпиады.

Рассмотрим пример проведения обучающей олимпиады в основной школе по теме «Тайны графов».

Олимпиада должна способствовать формированию умений применять графы при решении задач и умения использовать эти знания в жизни; формированию графических и логических умений.

Временной промежуток – один месяц.

Первая неделя. Понедельник. Регистрация команд и вручение первого задания: подготовить визитку команды, используя средства ИКТ. Три-четыре дня на подготовку и в пятницу-конкурс визиток.

Вторая и третья недели. Обучающий тур.

Участники получают задания по теме «Теория графов» и теоретический материал для ознакомления [1].

Задача 1.

В школьном драмкружке решили ставить гоголевского «Ревизора». И тут разгорелся жаркий спор. Все началось с Ляпкина-Тяпкина.

-Ляпкиным-Тяпкиным буду я! – решительно заявил Гена.

-Нет, я буду Ляпкиным-Тяпкиным, - возразил Дима. - С раннего детства мечтал воплотить этот образ на сцене.

-Ну хорошо, согласен уступить эту роль, если мне дадут сыграть Хлестакова, - проявил великодушие Гена.

-…А мне – Осипа, -не уступил ему в великодушии Дима.

-Хочу быть Земляникой или Городничим, - сказал Вова.

-Нет, Городничим буду я, - хором закричали Алик и Боря. – Или Хлестаковым, - добавили они одновременно.

Удастся ли распределить роли так, чтобы исполнители были довольны?

Решение.

Попробуем построить граф для ситуации, описанной в задаче «Кто играет Ляпкина-Тяпкина?». Изобразим юных актеров кружками верхнего ряда: А — Алик, Б — Боря, В — Вова, Г — Гена, Д — Дима, а роли, которые они собираются играть, кружками второго ряда (1 — Ляпкин-Тяпкин, 2 — Хлестаков, 3 — Осип, 4 — Земляника, 5 — Городничий). Затем от каждого участника проведем отрезки, т. е. ребра, к ролям, которые он хотел бы сыграть. У нас получится граф с десятью вершинами и десятью ребрами (рис.).

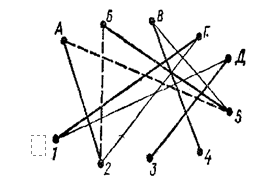
Рис.1

Чтобы решить задачу, нужно из десяти выбрать пять ребер, не имеющих общих вершин. Сделать это легко. Достаточно заметить, что в вершины 3 и 4 ведет по одному ребру, из вершин Д и В соответственно. Это означает, что Осипа (вершина 3) должен играть Дима (кто же еще?), а Землянику — Вова. Вершина 1— Ляпкин-Тяпкин — соединена ребрами с Г и Д. Ребро 1 — Д отпадает, так как Дима уже занят, остается ребро 1- Г, Ляпкина-Тяпкина должен играть Гена. Остается соединить вершины А и Б с вершинами 2 и 5, соответствующими ролям Хлестакова и Городничего. Это можно сделать двумя способами: либо выбрать ребра А — 5 и Б — 2, либо ребра А - 2 и Б - 5. В первом случае Алик будет играть   Городничего, а   Боря — Хлестакова, во   втором случае наоборот. Как показывает наш граф, других решений задача не имеет.

Ответ. Да, роли можно распределить согласно желаниям актеров.

Задача 2.

Докажите, что не существует графа с пятью вершинами, степени которых равны 4,4,4,4,2.

Доказательство.

Поскольку из всех вершин, кроме одной выходит по 4 ребра, то и из пятой вершины также должно выходить четыре ребра.

Задача 3.

В некотором королевстве было 32 рыцаря. Некоторые из них были вассалами других. Рыцарь, имевший не менее четырёх вассалов, носил титул барона. Вассал может иметь только одного барона, причём барон всегда богаче своего вассала. Какое наибольшее число баронов могло быть при этих условиях? (В королевстве действовал закон: "вассал моего вассала - не мой вассал").

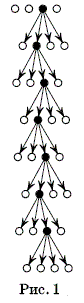
Решение. Предположим, что имелось не менее восьми баронов. Тогда, поскольку каждый из них имел не менее четырёх вассалов, их вассалами являлись не менее 32 рыцарей (общих вассалов бароны не могли иметь по условию). Кроме того, самый богатый рыцарь, если таких несколько, то каждый из них не может быть ничьим вассалом. Получаем, что было не менее 33 рыцарей — это противоречит условию. Теперь покажем, что 7 баронов могло быть. На рисунке рыцари отмечены кружками, стрелки ведут от каждого барона к его вассалу. Кружочки, соответствующие баронам, закрашены. Ответ. 7 баронов

Задача 4.

Посёлок построен в виде квадрата 3 квартала на 3 квартала (кварталы - квадраты со стороной b, всего 9 кварталов). Какой наименьший путь должен пройти асфальтоукладчик, чтобы заасфальтировать все улицы, если он начинает и кончает свой путь в угловой точке A? (Стороны квадрата - тоже улицы).

Решение.

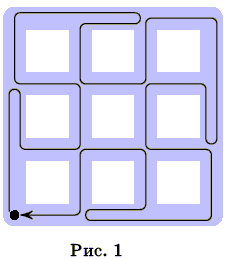
Рис.3.

Опишем решение в виде графа, где улицы – ребра, перекрестки - вершины (рис.).  Понятно, что длина маршрута асфальтоукладчика не меньше 24, так как он должен проехать по каждой улице хотя бы один раз.  Восемь вершин имеют нечетную степень(3) и ровно на восьми перекрёстках пересекается нечётное число улиц. Следовательно, из закономерности 5 начертить граф, не отрывая карандаша, невозможно, и любой кольцевой маршрут асфальтоукладчика должен проходить по каким-то улицам дважды, т.е. по 8/2 = 4 улицам. Ответ. Минимальная длина маршрута асфальтоукладчика равна 28.

Задача 5.

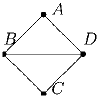
Рис.4.

На карте обозначено 4 деревни: A, B, C и D, соединённые тропинками (см. рисунок). В справочнике написано, что на маршрутах A–B–C и B–C–D по 10 колдобин, на маршруте A–B–D – 22 колдобины, а на маршруте A–D–B – 45 колдобин. Туристы хотят добраться из A в D так, чтобы на их пути было как можно меньше колдобин. По какому маршруту им надо идти? Не забудьте доказать, что на указанном Вами маршруте действительно меньше всего колдобин.

Решение.

Всего есть три пути, которые могут оказаться кратчайшими:

1. A – D;
2. A – B – D;
3. A – B – C – D;

Из того, что на маршруте A – B – D находятся 22 колдобины, следует, что на тропинке B – D никак не больше 22 колдобин, стало быть из 45 колдобин маршрута A– D – B хотя бы 23 на тропинке A – D, то есть второй путь выгоднее первого.

Аналогично, поскольку на маршруте A – B – C 10 колдобин, то на тропинке A- B не более 10 колдобин. Значит из 22 колдобин пути A – B - D не менее 12 приходится на тропинку B – D. Но на пути B – C – D всего 10 колдобин, поэтому третий путь выгоднее второго, а, значит, и первого. Ответ. Им надо идти по маршруту A–B–C–D.

Задача 6.

В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

Решение.

Предположим, что это возможно. Рассмотрим тогда граф, вершины которого соответствуют телефонам, а ребра – соединяющим их проводам. В этом графе 15 вершин, степень каждой из которых равна пяти. Подсчитаем количество ребер в этом графе. Для этого сначала просуммируем степени всех его вершин. Ясно, что при таком подсчете каждое ребро учтено дважды (оно ведь соединяет две вершины!). Поэтому число ребер графа должно быть равно 15 • 5/2. Но это число нецелое! Следовательно, такого графа не существует, а значит, и соединить телефоны требуемым образом невозможно. Ответ.Соединить телефоны требуемым образом невозможно.

Задача 7.

Школьник сказал своему приятелю Вите Иванову: «У нас в классе тридцать пять человек. И представь, каждый из них дружит ровно с одиннадцатью одноклассниками...». «Не может этого быть» - сразу ответил Витя Иванов, победитель математической олимпиады. Почему он так решил?

Решение.

Представим себе, что между каждыми двумя друзьями протянута ниточка. Тогда каждый из 35 учеников будет держать в руке 11 концов ниточек, и значит, всего у протянутых ниточек будет 11* 35 = 385 концов. Но общее число не может быть нечётным, так как у каждой ниточки 2 конца. Ответ. Невозможно начертить граф с нечетным числом нечетных вершин.

Задача 8.

В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли добраться из города 1 в город 9?

Решение.

1. Двузначные числа, которые делятся на 3: 12, 15, 18, 21,24,27, 30,33, 36,39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99. Построив граф, можно увидеть пути из 1 города в 9.

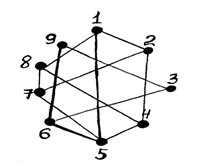
Рис.5.

Ответ. Можно (см. рисунок)

Задача 9.

«Проказница мартышка, осел, козел да косолапый мишка затеяли сыграть квартет». Мартышка расположилась напротив медведя, а слева и справа от нее – осел и козел. «Ударили в смычки, дерут, а толку нет». Тогда осел и козел поменялись местами. «Расселись, начали квартет. Он все-таки на лад нейдет». Таким образом они перепробовали все возможные варианты. Медведь всегда оставался на одном месте. Сколько всего было вариантов расположения незадачливых музыкантов?

Решение.

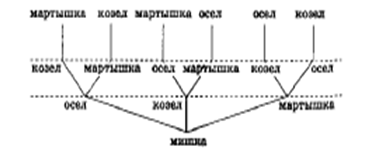
Рис.6.

Ответ. 6 вариантов

Задача 10.

Джон, приехав из Диснейленда, рассказывал, что там на заколдованном озере имеются 7 островов, с каждого из которых ведет 1, 3 или 5 мостов. Верно ли, что хотя бы один из этих мостов обязательно выходит на берег озера?

Решение.

Предположим, что острова - вершины графа. Тогда по закономерности 3 о числе  нечетных вершин их количество в графе четно.  Островов 7 и каждый из них имеет нечетную степень, т. е. нарушается теорема о числе нечетных вершин. Поэтому должно быть либо 8 островов, либо мост  на берег озера. 

Ответ. Да

Задача 11.

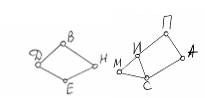
Рис. 7.

В деревне Ивановка  9 домов. Известно, что у Петра соседи Иван и Антон, Максим сосед Ивану и Сергею, Виктор – Диме и Никите, а также по соседству живут Евгений с Никитой, Иван с Сергеем, Евгений с Димой, Сергей с Антоном и больше соседей в означенной деревне нет (соседними считаются дворы, у которых есть общий участок забора). Может ли Петр огородами пробраться к Никите за яблоками?

Решение.

Нет, так как граф не связный.

Задача 12.

Четыре девочки – Катя, Вера, Маша и Аня – участвовали в конкурсе «Старая калоша». В каждом из туров участвовали 3 девочки. Катя участвовала в 8 турах – больше всех, а Вера в 5 турах – меньше всех. Сколько было туров?

Решение.

6 туров. Т.к. в каждом туре участвуют 3 девочки, то они могут принимать участие в разном составе, например, Катя может участвовать в первом туре трижды (Катя, Вера, Аня; Катя, Аня, Маша; Катя, Вера, Маша). Таким образом,  после участия во втором туре в разных составах Вера сыграет 5 туров, и в оставшихся принимают участие  Катя, Аня, Маша. Решение задачи легко получить, построив граф. Ответ. 6 туров

Задача 13.

На рисунке изображены расстояния между пунктами А, В, С, D, E и  F. Двигаться по дорогам можно только в направлениях, указанных стрелочками. Водитель едет из пункта А в пункт D. Каково минимальное расстояние, которое он может преодолеть?

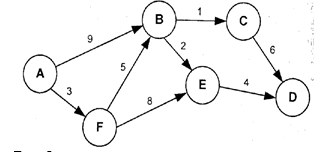
Рис.8.

Решение.

Рассмотрим последовательно возможные пути поездки и сравним их расстояния. АВСD=16, АВЕD=15, АFВСD=15, АFВЕD=14, АFЕD=15. Выбираем минимальное расстояние. Оно равно 14. Ответ. 14

Задача 14.

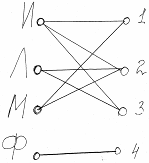
Рис.9.

 Необходимо составить фрагмент расписания для одного дня с учетом следующих обстоятельств:

1. учитель истории может дать либо первый, либо второй, либо третий уроки, но только один урок;
2. учитель литературы может дать один, либо второй, либо третий урок;
3. математик готов дать либо только первый, либо только второй урок;
4. преподаватель физкультуры согласен дать только последний урок.

Сколько и каких вариантов расписания, удовлетворяющего всем вышеперечисленным условиям одновременно, может составить завуч школы?

Решение.

Без сомнения, эту задачу можно решить путем обыкновенного перебора всех возможных вариантов, но решение будет наиболее простым, если вычертить граф в виде дерева. Ответ: 3 варианта: ИМЛФ, МИЛФ, МЛИФ.

Обучающий тур может быть проведен в виде  олимпиады (как внутрикомандной, так и внутришкольной), привлекая  к обсуждению вопросов этой темы и решению задач не только учащихся, входящих в состав команды. Учитель может сформировать по своему усмотрению мини-команды (например, поделить класс на группы или работать с классами одной параллели). Далее необходимо ознакомить учащихся с заданиями и согласовать направления деятельности: что искать и где искать (поиск информации в библиотеке или Интернет), написание ответов, оформление и т.п. Внутри мини-команды возможно деление учащихся на группы по направлениям поиска (где искать и что искать?) с учетом пристрастий и интересов учащихся.

В ходе выполнения заданий члены мини-команды обмениваются между собой результатами своей деятельности и производят сравнительную проверку. Получив правильные ответы от организаторов, следует подвести итоги работы каждой группы. По итогам можно (и очень желательно) провести мини-конференцию, круглый стол, открытый урок, нечто вроде защиты творческих работ, где ребята обменяются мнениями, обсудят работу и получат комментарии учителя (по содержанию и организации). Очень важно побеседовать по этой теме.

Возможен любой творческий подход к проведению обучающего тура в своей команде (это может быть КВН, экскурсия/поход, игра и т.п.).

Команда пишет "отчет" о проделанной работе. В нем можно кратко описать:

• как проходил обучающий тур в вашей команде;

• как были распределены обязанности между членами команды, и каким образом они были выполнены;

• какие источники информации были использованы, и какие из них, на ваш взгляд, оказались более полезными и полными;

• какое задание было самым трудным, какое легким, над каким было интереснее всего работать;

• какова была роль лидера (капитана) команды;

• какую роль сыграл руководитель команды (учитель математики) в организации работы в рамках обучающего тура.

Знакомство с понятием граф возможно через объяснение учителя. Пример такого занятия.

Тема: Первая встреча с графом

Цель: познакомить учащихся с понятием «граф», научить учащихся определять, изображать и составлять графы, которые можно вычерчивать без отрыва карандаша от бумаги.

Оборудование: цветной мел и карандаши, мультимедийный проектор, презентация «Первая встреча с графом», карточки с домашним заданием.

Ход занятия.

1) Учитель просит ребят разбиться на группы по 4-5 человек.

2) Учитель показывает 1-й слайд презентации, где изображены два конверта: один – открыт, другой – закрыт. Учитель просит перерисовать их в тетрадь и другим цветом их обрисовать, не отрывая карандаша от бумаги и не проводя дважды ни по одной линии. Учащиеся приходят к выводу, что открытый конверт можно нарисовать, в отличие от закрытого.

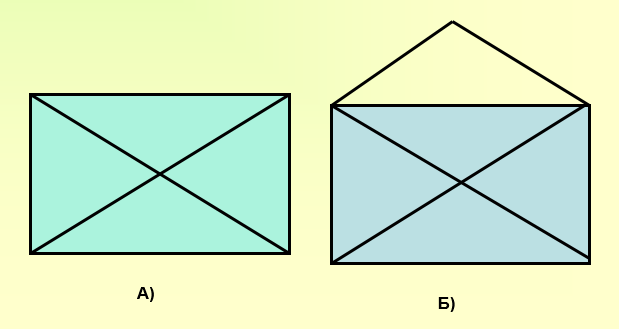
Рис.10.

3) Учитель предлагает обозначить точки пересечений, а в скобках написать, сколько линий выходит из той или иной точки пересечений, если четное, то поставить «ч», если – нечетное – «н». Показывает, как выполнить данную работу на 2-м слайде.

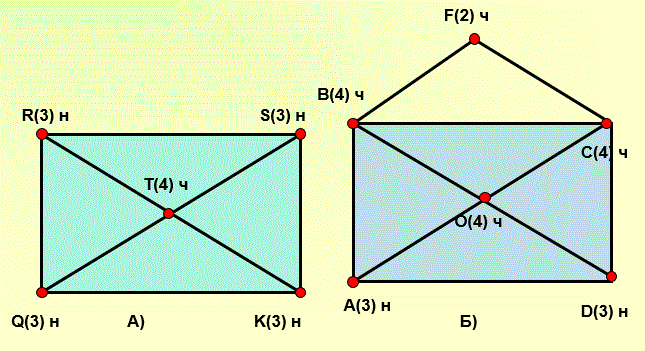
Рис.11.

4) Учитель включает 3-й слайд. На слайде изображены фигуры, представляющие собой окружности, в которых проведены линии и просит перерисовать их в тетрадь, обозначить, как и в предыдущем случае и попытаться обрисовать их не отрывая карандаш от бумаги и не проводя дважды ни одной линии. Учащиеся выполняют задание и приходят к выводу, что фигуры, изображенные на рисунках а); в); д) можно нарисовать одним росчерком не проводя ни одной линии дважды, а остальные – нельзя.

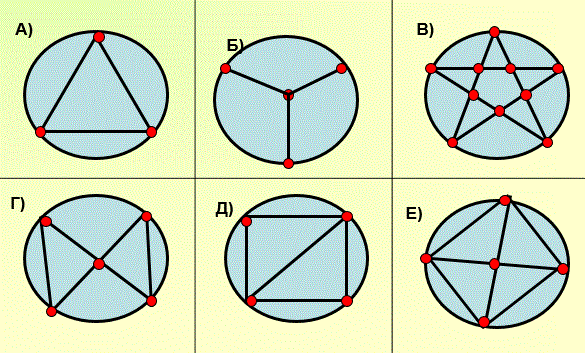
Рис.12.

5) Учитель просит учащихся выдвинуть гипотезу о том, в каком случае можно выполнить задание, а в каком нет. Выступает в роли координатора диспута. Если есть необходимость, помогает с помощью наводящих вопросов. Учащиеся высказывают свое мнение, делают предположение о том, что фигуру можно нарисовать, не отрывая карандаш от листа и не проводя дважды ни одной линии, если в одну точку можно войти столько же раз, сколько выйти из нее, за исключением быть может начала и конца пути.

6) Выдвигается гипотеза: фигуру можно нарисовать, не отрывая карандаш от листа и не проводя дважды ни по одной линии, если она содержит не более двух точек, из которых выходит нечетное число линий.

7) Учитель предлагает каждой группе придумать два рисунка, в одном из которых не более двух таких точек, а в другом – 3 или более. Задает вопрос: «Находит ли подтверждение выдвинутая гипотеза?» Учащиеся выполняют задание и приходят к выводу о подтверждении данной гипотезы.

8) Учитель показывает схему мостов Кёнигсберга. Слайд №4. Рассказывает легенду. Имеются исторические сведения о том, что три столетия назад жители тихого Кёнигсберга увлеченно решали задачу: требовалось найти маршрут, проходящий по всем четырем участкам суши по одному разу. При этом через каждый из мостов можно проходить только по одному разу, а конец и начало пути должны совпадать.

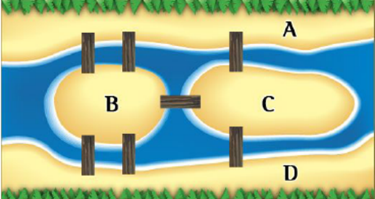
Рис.13.

9) Учащимся предлагается данный рисунок преобразовать в схему, состоящую из точек и линий и сделать вывод о возможности решения данной задачи. Учащиеся составляют схему, нумеруют точки и делают вывод о возможности решения.

10) Учитель продолжает рассказ. Этой головоломкой заинтересовался Леонард Эйлер (слайд №5). Слайд №6. Эйлер доказал, что маршрута, который бы отвечал условиям головоломки, не существует, и разработал теорию решения такого рода головоломок, давшую начало новому разделу математики, получившему название «теория графов».

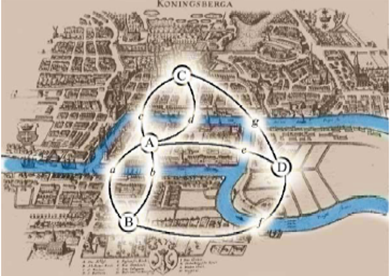
Рис.14.

11) Учитель вводит понятие «граф». Слайд №7. Схемы, состоящие из точек (кружков) и отрезков, соединяющих пары точек называют графами. Точки графа иначе называют вершинами графа, отрезки – ребрами графа. Ребра графа могут изображаться как прямыми, так и кривыми линиями, а точки могут располагаться произвольно.

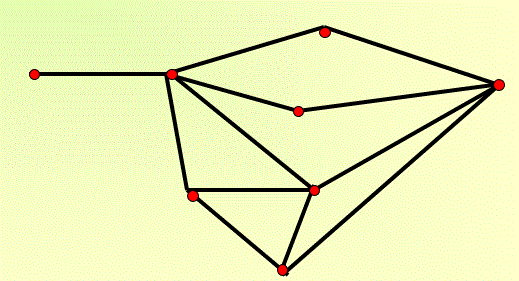
Рис.15.

 Так на слайде № 8 изображен один и тот же граф.

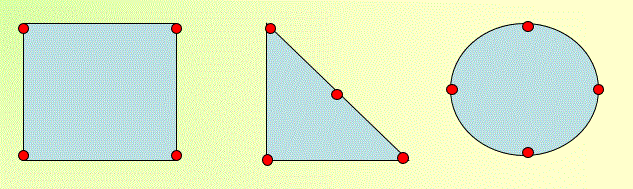
Рис.16.

 Если вершина графа не соединена с другими вершинами отрезками, ее называют изолированной. Слайд №9.

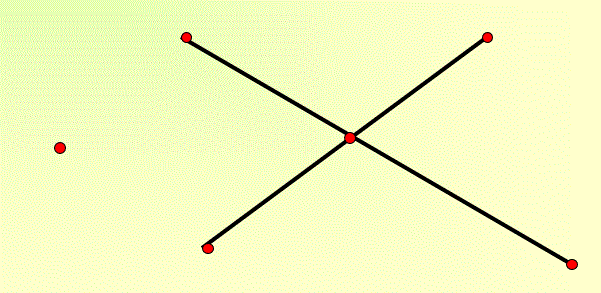
Рис.17.

 Если каждая вершина графа соединена отрезками со всеми остальными вершинами, то граф называется полным. Слайд №10.

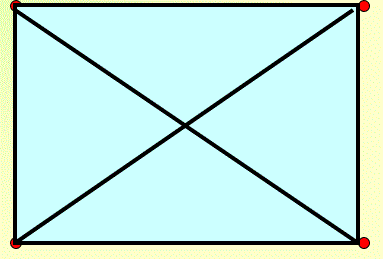
Рис.18.

12) Учитель просит учащихся самостоятельно выполнить задания:

1) Нарисовать граф с пятью вершинами и пятью ребрами (3 различных варианта). Слайд №11.

2) Нарисовать граф с четырьмя вершинами и пятью ребрами так, чтобы одна вершина была изолированной. Слайд №11.

3) Слайд №12.  Найти три пары одинаковых графов.

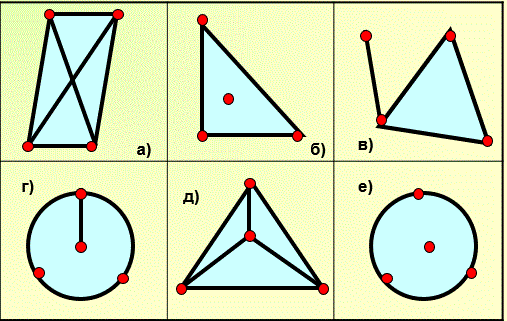
Рис.19.

13) Обсуждение решений в группе.

14) Учитель продолжает объяснение. В связи с задачей о Кёнигсбергских мостах возникло понятие эйлерова пути — так называется путь в графе, проходящий по каждому ребру графа ровно один раз. Если начало и конец эйлерова пути совпадают, то он называется эйлеровым циклом, а такой граф называется эйлеровым графом. Степенью вершины графа называется число ребер графа, которым принадлежит эта вершина. Слайд №13. Эйлер доказал, что граф будет иметь эйлеров цикл, если все его вершины имеют четную степень или граф содержит две нечетные вершины. Если же в графе количество нечетных вершин больше двух, то такой граф не обладает ни эйлеровым циклом, ни эйлеровым путем, его нельзя изобразить одним росчерком, не проходя дважды по одному и тому же ребру.

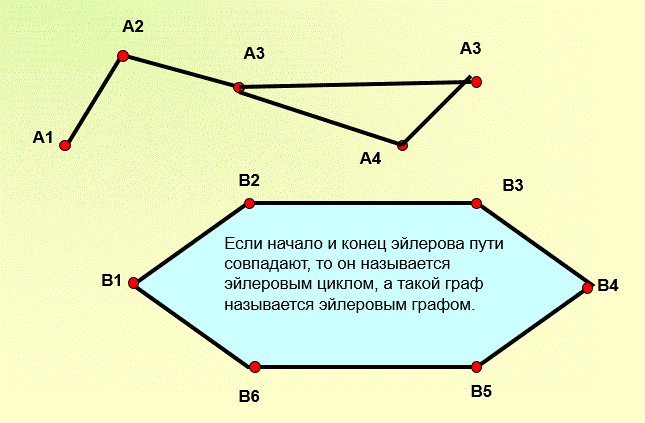
Рис.20.

15) Слайд №14. Задание: Найти на рисунке графы:

a) которые обладают эйлеровым циклом;

b) которые обладают эйлеровым путем;

c) которые не обладают ни эйлеровым циклом, ни эйлеровым путем.

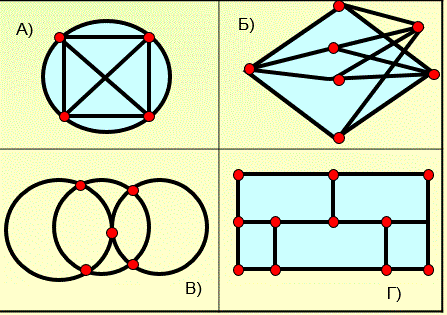
Рис.21.

16) Учитель просит посмотреть на графы слайда №15 и ответить на вопросы: можно ли их обойти и если можно, то с какой вершины начинать обход и какая окажется в конце пути.

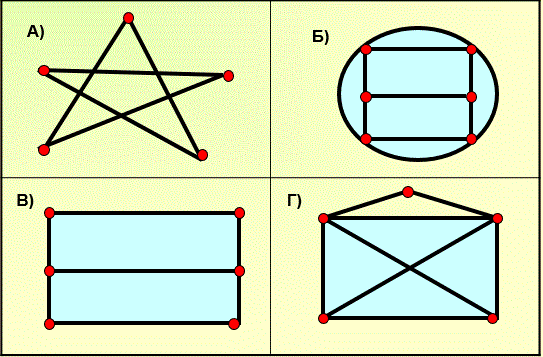
Рис.22.

17) В ходе дискуссии ребята формулируют гипотезу: если все вершины графа имеют четную степень, то тогда обход, о котором идет речь, возможен, и начать этот обход можно с любого участка. Если же из этих вершин две нечетные, то и тогда можно совершить обход, но только начало обхода должно быть взято в одной из этих двух вершин, а конец обхода будет во второй нечетной вершине.

18) Итоги занятия.

Учитель: «Попробуйте провести рефлексию сегодняшнего занятия.» Ученики: Познакомились с понятиями граф, ребро, вершина графа. Узнали какой граф можно обойти «одним росчерком», узнали о существовании раздела математики «теории графов», узнали о том, кто и когда основал данную теорию.

19) Домашнее задание (карточки).

1) Составить алгоритм решения задач, в которых необходимо обойти фигуру «одним росчерком».

2) Ответить на вопрос: можно ли фигуру, изображенную на рисунке нарисовать одним росчерком? Решить с помощью графа.

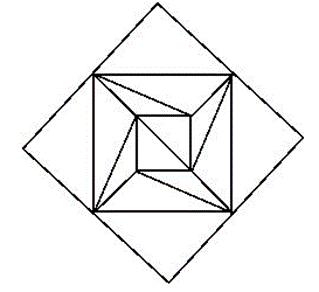
Рис.23.

3) Добавьте два моста так, чтобы получившуюся схему можно было

обойти, побывав на каждом мосту ровно один раз и вернувшись в исходную точку

Рис.24.

Четвертая неделя. Понедельник-четверг. Блиц-конкурс. Каждая команда выкладывает от 1 до 10 задач, которые могут быть решены с помощью понятия «граф». Задачи не должны повторяться, не должны быть из подборки обучающего тура. Решения каждая команда передает жюри и той команде, которая выложила задачу. Оценивается как выложенное количество задач, так и количество правильно решенных задач каждой командой. Команды – участники принимают участие в проверке и сдают протокол оценки соперников жюри.

Четвертая неделя. Пятница. Очный тур олимпиады. Зачет как индивидуальный, так и командный (по сумме набранных баллов первых 5 участников команды).

Примеры задач конкурсного тура [1].

Задача 1. В Простоквашинской начальной школе учится всего 20 детей. У любых двух из них есть общий дед. Докажите, что у одного из дедов в этой школе учится не менее 14 внуков и внучек.

Решение. Рассмотрим граф, вершины которого обозначают дедов, чьи внуки учатся в этой школе, а ребра – внуков (всего 20 ребер). Пусть а А и В- деды одного из внуков. Выделим также остальных внуков этих дедов (кратные ребра, соединяющие вершины А и В). По условию любые два ребра имеют общий конец, следовательно, каждое из остальных ребер выходит либо из вершины А, либо из В. Если все они выходят из одной вершины, то утверждение задачи очевидно, т.к. у деда 20 внуков. Иначе существует третья вершина С, где сходятся эти ребра. Значит, что всего имеется ровно три деда. Следовательно, найдутся две вершины из этих трех, соединенные ребром кратности не более шести (в противном случае граф должен иметь по крайней мере 3*7=21 ребро). Тогда у оставшегося деда по крайней мере 20-6=14 внуков.

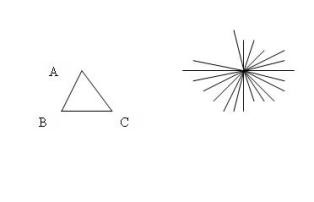
Рис.25.

Задача 2. В государстве 100 городов, и из каждого из них выходит 4 дороги. Сколько всего дорог в государстве?

Решение. Если в государстве100 городов (вершин графа), то сумма степеней всех вершин равна 4*100 = 400, и равна удвоенному произведению числа ребер – 2r. Отсюда число ребер (дорог): 400/2=200. Ответ: 200 дорог.

Задача 3. У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств?

Решение. Нет, не может. В противном случае получился бы граф соседства баронств с нечетным количеством нечетных вершин.

Задача 5. Можно ли фигуры на рисунке начертить одним росчерком пера?

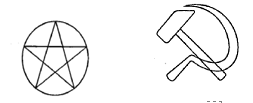
Рис.26.

 Решение. А). Все вершины данного графа - четные. Значит, начертить одним росчерком пера эту фигуру можно, причем обход можно начинать с любой вершины.

Б). Граф содержит две нечетные вершины.  Значит, начертить одним росчерком пера эту фигуру можно, причем обход необходимо начинать с одной из нечетных вершин, а закончить – в другой нечетной вершине. (Нечетные вершины у основания молотка).

Задача 5. Шесть островов на реке в парке "Лотос" соединены мостами.

Можно ли, начав прогулку на одном из островов, пройти по каждому из мостиков ровно один раз и вернуться на тот же остров? В случае отрицательного ответа определите, сколько мостиков и между какими островами нужно построить, чтобы такая прогулка стала возможной.

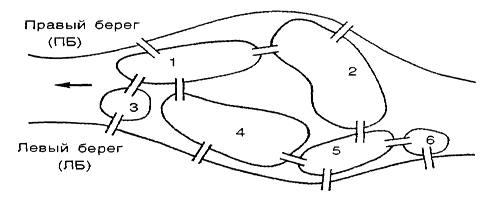
Рис.27.

Решение. Задача о мостах сводится к решению задачи о построении чертежа одним росчерком карандаша. Для решения этой задачи построим граф. В данной графе вершины – острова (с 1 по 6, как на карте), ребра – мосты.

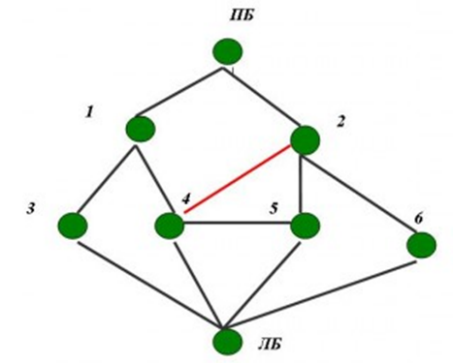
Рис.28.

Для того, чтобы данный обойти, не проходя по одному ребру дважды, должно выполняться следующее условие: все вершины графа должны быть вершинами четной степени.

Построим небольшую таблицу:

Таб.1.

Из таблицы видно, что две вершины графа имеют нечетные степени (вершины 2 и 4). Следовательно, пройти по каждому из мостов один раз и вернуться на тот же остров, с которого начиналась прогулка, не удастся. Чтобы такая прогулка состоялась необходимо построить мост между островами 2 и 4.

В качестве домашнего задания можно участникам предложить такую творческую задачу: изобразите в виде графа Солнечную систему, которая включает планеты и их спутники: Марс со спутниками Деймос и Фобос; Земля со спутником Луна; Меркурий; Венера; Юпитер со спутниками Ганимед, Каллисто, Европа, Ио; Плутон со спутником Харон; Уран со спутниками Оберон, Титания; Сатурн со спутником Титан; Нептун со спутником Тритон.

Решения окажутся различными. Можно организовать выставку рисунков - решений в день подведения итогов. Можно предложить учащимся выполнить исследовательскую работу или сделать проект, основанный на применении графов.

По сути, проведение обучающей олимпиады, приводит к деятельностному погружению учащихся класса, параллели, школы в течение какого-то промежутка времени в какую-то определенную тему математики (графы, сюжетные задачи, функции, задачи на построение и т.д.). Ребята, вовлеченные в такую работу, приобретают социальное, личностное, познавательное и коммуникативное развитие, что обеспечивает широкие возможности учащихся для овладения ими знаний, умений, навыков, компетентностей.  Развивается способность к познанию мира, обучению, сотрудничеству, самообразованию и саморазвитию. В ходе обучающей олимпиады участники самостоятельно занимаются своим обучением и получают нужную информацию из разных источников, работают в группах и принимают решения, используют новые технологии получения информации и коммуникации, все это приводит к формированию Универсальных Учебных Действий (УУД).

Проведение обучающей олимпиады может стать формой организации внеурочной деятельности с обучающимися в школе.

Ссылки на источники:

 1. МОУ ДПОС «Центр медиаобразования», г. Тольятти. http://wiki.tgl.net.ru/index.php/Категория:Проект_ДООМ – 2007-2008 (1 цикл)