Аннотация. В статье представлено занятие математического кружка в 6 классе, которое рассчитано на 3 часа. В содержании подобраны задания, которые знакомят учащихся с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результате вычислений. Освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления. Новые способы умножения развивают у учащихся огромный интерес к предмету.
Ключевые слова: дополнительное математическое образование школьников, внеурочная деятельность, математический кружок, способы умножения, решение задач, развитие творческих способностей, развитие интереса к предмету.
Математика - одна из основных наук. Правильное её изучение приводит не только к умению считать, но и к умению логически мыслить. Внеурочная деятельность школьников – это совокупность всех видов деятельности школьников, в которой в соответствии с основной образовательной программой образовательного учреждения решаются задачи воспитания и социализации, развития интересов, формирования универсальных учебных действий (УУД).
Внеурочная деятельность является неотъемлемой частью образовательного процесса в школе и позволяет реализовать требования федерального государственного образовательного стандарта (ФГОС) в полной мере. Особенностями данного компонента образовательного процесса являются предоставление обучающимся возможности широкого спектра занятий, направленных на их развитие. Эффективность внеурочной деятельности определяется правильным выбором форм и методов проведения, учитывающим профиль обучения школьников, уровень их математической подготовки, интерес к изучаемому предмету и т. п. Учителю математики необходимо использовать новые приемы, технологии не только в процессе обучения, но и в организации внеурочной работы. Математический кружок – одна из самых емких постоянных форм организации внеурочной работы. Кружок формируется из учащихся, проявивших интерес к изучению математики, стремящихся к обогащению своих знаний, к совершенствованию своих математических навыков и умений. Занятия математического кружка направлены на развитие одаренных детей, углубление знаний учащихся, получаемых ими при изучении основного курса, развитие познавательного интереса к предмету, любознательности, смекалки, расширение кругозора, вырабатывают у них навыки самостоятельного получения знаний, учат ориентироваться в потоке различной информации.
На каждом занятии проводится коллективное обсуждение решения задач определенного вида. На этом этапе у детей формируется такое важное качество, как осознание собственных действий, самоконтроль, возможность дать отчет в выполняемых шагах при решении задач любой трудности. Ребенок на этих занятиях сам оценивает свои успехи. Это создает особый положительный эмоциональный фон: раскованность, интерес, желание научиться выполнять предлагаемые задания. В системе заданий реализован принцип «спирали», то есть возвращение к одному и тому же заданию, но на более высоком уровне трудности.
Ускоренный прогресс во всех областях знаний и деятельности требует появления большего числа исследователей-творцов. Вот почему так важно, чтобы дети учились не только запоминать и усваивать определенный объем знаний, но и овладели приемами исследовательской работы, научились самостоятельно добывать знания, ставить перед собой цели и упорно добиваться результатов. Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как сохранить у школьников интерес к изучаемому материалу, поддержать их активность на протяжении всего занятия. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мышление обучающихся, стимулировали бы их самостоятельность в приобретении знаний.
Удачным с этой точки зрения, представляется на занятиях кружка, применение такого вида эвристической деятельности, как математическое исследование необычных способов умножения.
В данной статье предлагается разработка занятия по математике в шестом классе.
Введение. Сегодня, ребята, мы с вами познакомимся с увлекательной темой: «Необычные способы умножения».
Введение.
Учитель: «Способы выполнения арифметических действий в старину не всегда были так просты и удобны, так прямо и быстро приводили к результату. Наши предки пользовались гораздо более громоздкими и медленными приемами.
Умножение на пальцах.
Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством.
Для этого на одной руке вытягивали столько пальцев, на сколько, первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56. Так можно вычислять произведение любых однозначных чисел, больше 5 [1].
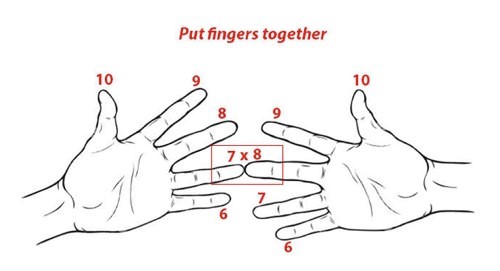
Рисунок 1: Умножение на пальцах.
Умножение на 9.
Умножение для числа 9: 9·1, 9·2 … 9·9 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки Допустим, хотим умножить 9 на 7. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 7. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 6 пальцев не загнуто, справа — 3пальца. Таким образом, 9·7 = 63. Еще пример: нужно вычислить 9·9 =?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 9-ю клеточку. Слева осталось 8 клеточек, справа — 1 клеточка. Значит 9·9 = 81. Все очень просто. 8 клеток и 1клетка[2].
Таблица Оконешникова
Умножение не стоит на месте, о чем доказывает новый способ умножения, который разработал Василий Иванович Оконешников. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе и «теперь ребята смогут умножать и складывать в уме не только единицы, десятки, но также миллионы, триллионы и даже, не пугайтесь, секстиллионы с квадриллионами»
7 8 9
4 5 6
1 2 3
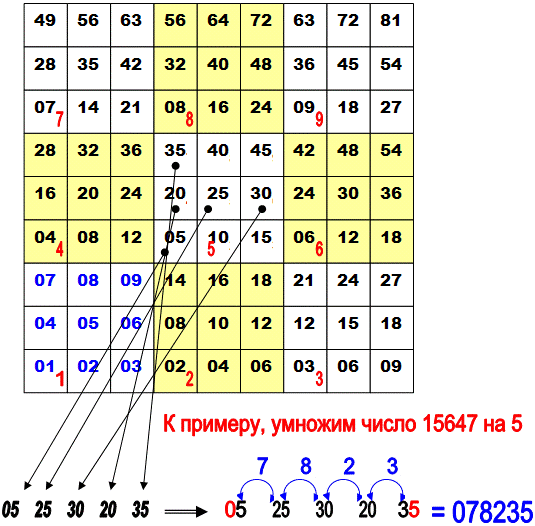
При этом каждая кнопка делится еще на 9 квадратов, в которой записываются результаты перемножения числа данной кнопки на числа от одного до девяти, т.е. получаем своеобразную таблицу умножения. Данный метод имеет ограничение - умножение делается на однозначное число. Например, найдем произведение чисел 148 и 4. Для этого обратимся к квадрату соответствующему четверке, выбираем числа, соответствующие цифрам числа по порядку: единице, четверке, восьмерке.
Получаем: 04 16 32. Левую цифру (в нашем примере - ноль) оставляем без изменений, а следующие складываем попарно: четверку с единицей, шестерку с тройкой.. Последняя цифра также без изменений. 0(4 + 1)(6+3)2 = 0592. Число 592 и есть результат умножения. Произведя расчет по методу Василия Ивановича Оконешникова при умножении многозначного числа на однозначное, этот метод достаточно прост и быстр, если имеется готовая таблица в уме или перед глазами.
 [3]
[3]
Рисунок 2: Таблица Оконешникова.
3. Русско-крестьянский способ умножения.
Сущность его в том, что умножение любых двух чисел сводится к ряду
последовательных делений одного числа пополам при одновременном умножении на 2 другого числа.
Пример: 32 х 13 = 416 Таблица 1
|
1 Множитель =32 |
II Множитель = 13 |
|
32 |
13 |
|
16 |
26 |
|
8 |
52 |
|
4 |
104 |
|
2 |
208 |
|
1 |
416 |
Способ умножения «метод решетки»

Рисунок 3: Способ умножения «метод решетки».
Для умножения чисел Мухаммед из Хорезма предлагал «метод решетки», который, пожалуй, проще, чем применяемый в школе[4]. Пусть надо умножить 564 на 37. Начертим таблицу, и запишем над ней число 564 слева направо, а справа от нее число 37 сверху вниз. В каждую клеточку запишем произведение цифр. При этом цифру десятков произведения запишем над косой чертой, а цифру единиц под ней. А теперь будем складывать числа в каждой косой полосе, выполняя, эту операцию справа налево. Если сумма окажется меньше 10, то ее пишут под нижней цифрой полосы. Если же окажется больше 10, то пишут только цифру единиц суммы, а цифру десятков прибавляют к следующей сумме. В результате получим нужное произведение, которое равно 20868, также выполняем умножение 623 ∙ 26 = 16198.
Китайский способ умножения.
А теперь представим метод умножения, бурно обсуждаемый в Интернете, который называют китайским. При умножении чисел считаются точки пересечения прямых, которые соответствуют количеству цифр каждого разряда обоих множителей.
Пример: умножим 32на 24. В первом множителе 3 десятка и 2 единицы, значит, строим 3 параллельные прямые и поодаль 2 прямые.
Во втором множителе 2 десятка и 4 единицы. Строим параллельно 2 и поодаль 4 прямые, пересекающие прямые первого множителя.
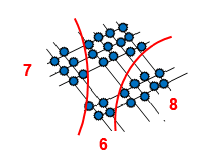
Рисунок 4: Китайский способ умножения.
Прямые пересеклись в точках, количество которых и есть ответ, то есть
32 • 24 = 768
Умножение двухзначных чисел на 11.
При умножении двухзначного числа на 11 возможны два случая.
Сумма цифр числа, умножаемого на 11, меньше 10. В этом случае надо между ними вставить их сумму:
14 • 11 = 1(1 + 4)4 = 154
81 • 11 = 8(8 + 1)1 = 891
39 • 11 = 3(3 + 9)9 = 429
Сумма цифр числа, умножаемого на 11, больше 9. В этом случае надо между ними вставить количество единиц в сумме цифр данного числа, а первую цифру множимого числа увеличить на 1:
38 • 11 = (3 + 1)18 = 418
96 • 11 = (9 + 1)56 = 1056
47 • 11 (4 + 1)17 = 517
Можно сразу провести соревнование между учащимися кто быстрее посчитает устно, применяя изученный прием. Результат, как правило, приводит ребят в восторг! [5]
Умножение двухзначных чисел, близких к 100
Пример: 94 • 78
Решение: чтобы получить необходимые последние цифры (единицы и десятки), необходимо:
100 – 94 = 6
100 – 78 = 22 и результаты перемножить
6 · 22 = 132 32 последние две цифры (1 запоминаем)
Чтобы получить первые две цифры (тысячи и сотни), надо: 94 – 22 = 72
72+1 = 73
В результате имеем 94•78 = 7332
Пример: 67 • 93
100 – 67 = 33
100 – 93 = 7
33 • 7 = 231 (31 последние две цифры) 2 запоминаем
67 – 7 = 60
60 + 2 = 62
67 • 93 = 6231
Удивительное умножение
Учащимся предлагается сначала умножить 12 345 679 • 9, затем на18, 27,…,81.
В результате учащиеся делаю вывод, что все числа кратны 9.
12345679 • 9 = 1111111 111
12 345 679 • 18 = 2 222 222 222
12 345 679 • 27 = 3 333 333 333
12 345 679 • 36 = 4 444 444 444
12 345 679 • 45 = 5 555 555 555
12 345 679 • 54 = 6 666 666 666
12 345 679 • 63 = 7 777 777 777
12 345 679 • 72 = 8 888 888 888
12 345 679 • 81 = 9 999 999 999
Умножение на 9, 99, 999, 9999, 99999
Учащимся предлагается (в виде соревнования) выполнить умножение различными способами:
Умножение столбиком
786 • 9 = 786(10 - 1) = 786 • 10 – 786 = 7860 – 786 = 7074 (для умножения многозначного числа на 9 надо приписать к нему справа нуль и вычесть из результата множимое число). При умножении на 99, приписывают два нуля, на 999, приписывают три нуля и т.д.
456 • 99 = 45600 – 456 = 45144
598 • 999 = 598000 – 598 = 597402
Следующий способ вызывает у учащихся огромный интерес, удивление:
Учитель: Ребята, я на доске сейчас запишу четырехзначное число состоящие из девяток 9999, один из вас на доске запишет любое тоже четырехзначное число. Каждый из вас перемножит эти числа (время засекается). Учитель в это время быстро записывает ответ на листе бумаги или на доске. После выполнения умножения ответы сверяют… у ребят – восторг! Они просят еще задание. Можно дать теперь пятизначное число 99999.
99999 • 74586 = 7458525414
999999 • 683498 = 683497316502
В результате умножения, получается десятизначное число: первые пять цифр его есть умножаемое число, только уменьшенное на единицу, а остальные пять цифр «дополнения, первой пятерки.
Интересные ответы
1 • 1 = 1
11 • 11 = 121
111 • 111 = 12321
1111 • 1111 = 1234321
11111 • 11111 = 123454321
111111• 111111 = 12345654321
1111111 • 1111111 = 1234567654321
11111111 • 11111111 = 123456787654321
111111111 • 111111111 = 12345678987654321
При умножении числа 142857 на числа от 1 до 6 получается произведение, записанное теми же цифрами, переставленными в циклическом порядке:
142857 • 1 = 142857;
142857 • 2 = 285714;
142857 • 3 = 428571;
142857 • 4 = 571428;
142857 • 5 = 714285;
142857 • 6 = 857142.
При умножении числа 37037 на числа от 1 до 9 получается произведение, записанное периодическими цифрами. Затем полученное число умножьте на 3.
37037 • 1 = 37037
37037 • 2 = 74074
37037 • 3 = 111111
37037 • 4 = 148148
37037 • 5 = 185185
37037 • 6 = 222222
37037 • 7 = 259259
37037 • 8 = 296296
37037 • 9 = 333333
Восстановите пример на умножение натуральных чисел, если известно, что сумма цифр у обоих сомножителей одинакова.[6]
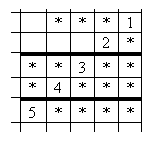
Рисунок 5: Задание на востановления пропущеных множетелей.
Ответ: 2221 • 25
Рассмотренные на занятиях способы умножения не такие сложные и могут повседневно использоваться учащимися. Они познавательны и интересны.
Ссылки на источники
- Мартин Гарднер Математические новеллы. – М.: Мир, 1974
- Мартин Гарднер Математические новеллы. – М.: Мир, 1974
- Л. Денисова Умножение натуральных чисел, журнал «Математика» №15 2011
- Л. Денисова Умножение натуральных чисел, журнал «Математика» №15 2011
- О.С. Шейнина, Г.М. Соловьева Математика. Занятия школьного кружка 5 - 6 класса, М.: НЦ ЭНАС, 2001
- П.В.Чулков Математика. Школьные олимпиады.5-6 класс. М.: НЦ ЭНАС, 2004

 Л.
В. Рутчина
Л.
В. Рутчина