О возможности обучения студентов основному курсу математики с применением пакетов прикладных программ

Предыдущая статья Следующая статья

Выпуск: Приложение 2. «Современные научные исследования: актуальные теории и концепции. Выпуск 6»

ART 570032

Авторы:

А. С. Котюргина,

Ю. Б. Никитин

Библиографическое описание статьи для цитирования:

Котюргина А. С., Никитин Ю. Б. О возможности обучения студентов основному курсу математики с применением пакетов прикладных программ // Научно-методический электронный журнал «Концепт». – 2017. – Т. 2. – С. 147–153. – URL: http://e-koncept.ru/2017/570032.htm.

Аннотация. В связи с сокращением аудиторных часов при неизменном объеме тем и разделов математики возникает вопрос об ином преподавании части разделов общего курса математики. В качестве альтернативы было предложено использование пакетов Maple и Mathcad, с помощью которых можно решить часть задач из общего курса математики. Содержание курсов дисциплин и порядок их изучения в высшей школе обусловлено образовательным стандартом, поэтому и изучение пакетов программ и изучение разделов курса математики нужно было вести одновременно. В статье, на примере задач линейной алгебры, рассматривается возможность преподавания математики и пакета Maple для студентов технических и нетехнических направлений. В результате такого преподавания математики авторы пришли к выводу, что студенты хорошо решают задачи на вычисление, но с приложениями справляются плохо. –Вывод этого исследования таков: в первом семестре первого курса нужно знакомить студентов с пакетами программ, а затем уже решать задачи из общего курса математики.

Ключевые слова: maple и mathcad, математическая подготовка, обучение линейной алгебре

Полный текст статьи

Печать

Есть два веских ограничения эффективное математическое образование в высшем учебном заведении: упадок математической подготовки, а также преобладание учебно-традиционного пассивного режима лекционного обучения [1]. В статье представлены результаты исследования о проведении ряда занятий по математике как в традиционной форме, так и с применением пакетов прикладных программ.

Направления математической подготовки студентов всех специальностей в высшей школе определяются согласно ФГОС 3 и ФГОС 3+. Согласно этим программам, часы для студентов инженерных специальностей таковы: 2 часа лекций и 2 часа практических занятий в неделю в первом и втором семестрах, 2 часа лекций и 1 час практических занятий в неделю в третьем и четвертом семестрах. Для студентов неинженерных специальностей число часов меньше в два или в четыре раза в зависимости от направления подготовки.

Совершенно очевидно, что с таким количеством часов, изложение материала носит ознакомительный и иллюстративный характер. В связи с этим был предложен несколько иной подход к обучению студентов.

«… задачей преподавателя является не столько научить вычислять детерминант, предел, производную, интеграл и т. д., сколько дать определения детерминанта, предела, производной, интеграла и т. д., и научить студентов вычислять их в простейших случаях» [2]. Чтобы более сложные задачи студенты могли решить в пакетах программ Maple и MathCad. Этим вопросам также посвящены работы [3–7].

В курсе «Математика» эти пакеты можно использовать при изучении всех разделов дисциплины. А именно: на лекциях вводить определения, доказывать теоремы и, кроме того, рассказывать, как эти задачи можно решать с применением пакетов Maple или Mathcad. А на практических занятиях активно пользоваться вычислительной техникой, то есть помимо занятий у доски, показывать вычисления в пакетах Maple или Mathcad. Для проведения этих занятий был разработан довольно подробный лабораторный практикум, цель которого – познакомить будущих специалистов с возможностями практического применения пакетов MathCad и Maple на занятиях. Сложность была только одна: студенты не были знакомы с вышеназванными пакетами. То есть пришлось изучать и пакеты программ и математику одновременно.

Студенты технических, гуманитарных, медицинских и фармацевтических направлений изучают следующие разделы математики на первом курсе:

Линейная алгебра.
Дифференциальное исчисление функции одной переменной. Изучение свойств функций и построение графиков.
Неопределенный интеграл.
Определенный интеграл. Приложения определенного интеграла.
Дифференциальное исчисление функции нескольких переменных.
Дифференциальные уравнения.

По всем темам студентам были заданы примеры, которые они должны были решить как аналитически (традиционно) так и в пакете прикладных программ.

Рассмотрим на примере линейной алгебры, какие задачи были решены студентами.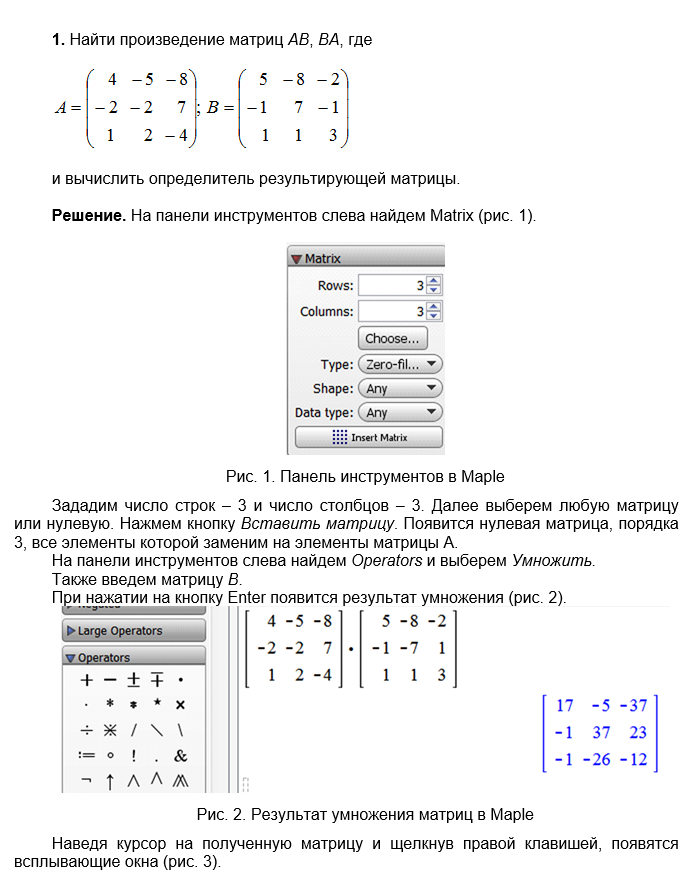

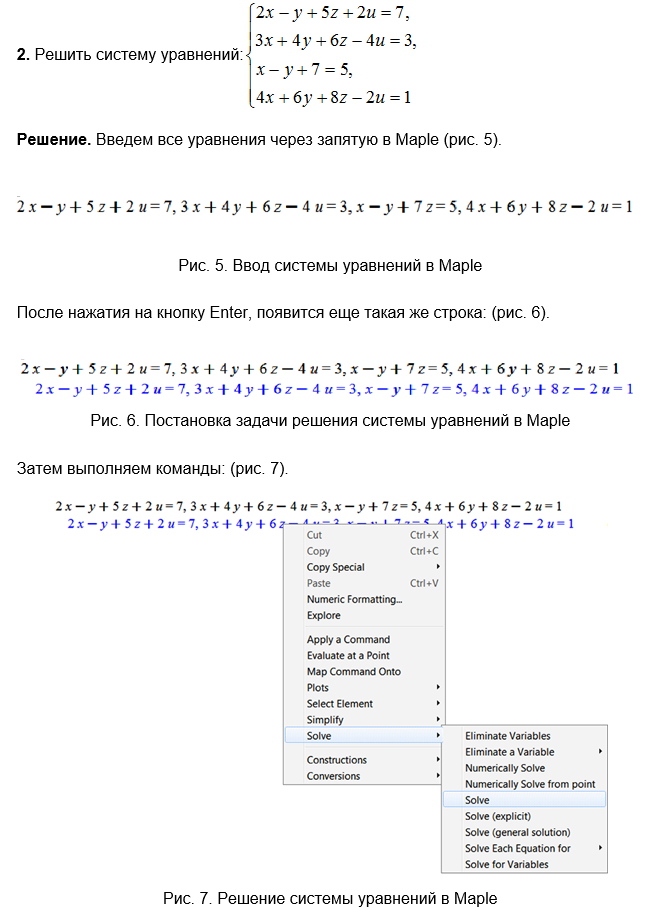
Такие указания были разработаны по всем темам, изучаемыми студентами [8]. С заданиями по линейной алгебре все студенты справились неплохо, хотя повторить все шаги вычислений без методических указаний удалось далеко не всем. Гораздо хуже были результаты при вычислении площадей, моментов инерции, длин дуг, исследовании функций и построении графиков. Это связано с многоступенчатостью задач. Так, чтобы найти длину дуги, нужно знать не только формулу ее вычисления, но и уметь расставлять пределы интегрирования в определенном интеграле.

Студентам нетехнических направлений нужно научиться решать только вычислительные задачи, с чем они и справились. Кроме этого, они познакомились с интерфейсом математического пакета, что в дальнейшем поможет им разобраться с интерфейсом, к примеру, программы IDENT для стоматологии.

Студентам технических направлений нужно научиться решать не только вычислительные задачи, поскольку в курсах физики, сопротивлении материалов, теории механизмов и машин и других они должны пользоваться математикой как хорошо знакомым инструментом.

Итак, студенты-первокурсники в начале своего обучения в высшей школе сталкиваются с большим объемом новой информации, массой заданий, и малым количеством аудиторных часов. Поэтому итогом первой сессии является почти 50 % неуспеваемость по математике. В качестве альтернативы классическому обучению математике был предложен вариант освоения программы по математике с использованием известных пакетов прикладных программ Maple или Mathcad. –

В результате такого обучения можно сделать вывод о том, что с вычислительными задачами все студенты справились неплохо. Для того, чтобы студенты научились решать прикладные задачи, нужны очень подробные методические указания как пользователям пакета прикладных программ, так и руководства к решению задач. Кроме того, изучение пакетов прикладных программ должно предварять изучение общего курса математики, чтобы студенты знали интерфейс программы и привыкли им пользоваться.

Список литературы

1. Zaleha Binti Ismail, Fereshteh Zeynivandnezhad, Yudariah Binti Mohammad, Eric David. Computing in Differential Equations with Mathematical Thinking Approach among Engineering Students, Kuching, Malaysia. April 11, 2014 to April 13, 2014, pp. 163–170. – ISBN 978-1-4799-3592-5

2. Котюргина, А. С. О применении пакетов прикладных программ в преподавании общего курса математики / А. С. Котюргина // Актуальные проблемы преподавания математики в техническом ВУЗе. – 2015. – № 3. – С. 76.

3. Алексенко, Н. В. Компьютерные технологии в обучении математике в условиях реализации ФГОС / Н. В. Алексенко, Н. А. Бурмистрова, Н. И. Ильина // Казанская наука. – 2013. – № 5. – С. 172–175.

4. Федорова, Е. И. Методические принципы преподавания математики студентам-социологам / Е. И. Федорова // Актуальные проблемы преподавания математики в техническом вузе. – 2015. – № 3. – С. 158–161.

5. Руппель, Е. Ю. Элементы теории вероятностей и методы статистической обработки экспериментальных данных : учеб. пособие / Е. Ю. Руппель. – Омск, 2003. – 141 с.

6. Cовершенствование процесса обучения математическим дисциплинам : отчет о НИР (промежуточ.) / Омский государственный университет путей сообщения ; рук. Беленкова Ж. Т. ; Окишев С. В., Шантаренко В. Г., Филимонова Т. А. [и др.]. – Омск, 2014. – 129 с. – № ГР 01201062509.

7. Котюргина, А. С. Методика проведения занятий по математике для студентов нетехнических направлений с использованием пакетов прикладных программ / А. С. Котюргина, Ю. Б. Никитин // Концепт : науч.-метод. электрон. журн. – 2016. – № 6. – С. 47–55.

8. Никитин, Ю. Б. Использование программ математического моделирования и расчетов для преподавания математики студентам медицинских вузов / Ю. Б. Никитин // Актуальные проблемы преподавания математики в техническом ВУЗе. – 2015. – № 3. – С. 132.

Комментарии

Чистоедова Ю. А., 2017-05-11 22:27:50 #

Обучение применению пакетов прикладных программ не дает знаний, сводит обучение к принципу "зачем учить человека считать и выполнять операции сложения, вычитания, умножения, деления и т.д., когда можно научить пользоваться калькулятором".

Оставить комментарий

Войдите или зарегистрируйтесь, чтобы комментировать.