Роль математического образования всем известна с давних пор. Ведь математика – это не только база экономики и естественных наук, но и очень важный компонент интеллектуального развития школьников.
А. К. Мендыгалиева определяет нестандартные задачи, как задачи не имеющих общих правил и положений, определяющих точную программу их решения. В методике их смешивают с задачами повышенной сложности. «Решение нестандартной задачи предполагает от учащихся проведение исследования. В тоже время, если решение одной и той же задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методом его решения, то для другого ученика – решение этой же задачи происходит стандартным образом, так как он уже умеет решать такие задачи. Одна и та же задача по математике в начальной школе может быть нестандартной, а в основной школе она уже является обычной, то есть не повышенной сложности [1].
Содержание начального курса математики раскрывается учащимся через единую систему целесообразно подобранных задач. Значительное место в этой системе занимают текстовые задачи.
К сожалению, многие учителя придерживаются шаблонов, которые при решении такого рода задач ограничиваются только арифметическим и алгебраическим методом. Считается, что решение задач арифметическим методом подготавливает учащихся начальной школы к осознанному решению задач с помощью составления уравнения, то есть к алгебраическому методу.
Например, рассмотрим следующую задачу, которая легко решается с помощью арифметического метода:
«Два велосипедиста выехали одновременно навстречу друг другу с одинаковой скоростью. Через какое время они встретятся, если расстояние между ними 60 км, а скорость 15 км/ч?»
Арифметически эту задачу можно решить в 2 действия:
В первом действии мы выясняем, какова скорость сближения велосипедистов:
15 + 15 = 30 (км/ч)
Во втором действии мы выясняем, через какое время велосипедисты встретятся:
60 : 30 = 2 (ч)
Ответ: велосипедисты встретятся через 2 часа.
Но, на наш взгляд, при решении текстовых задач не стоит ограничиваться только этими двумя методами. Ведь часто бывает так, что серьёзное увлечение математикой начинается с решения какой-либо понравившейся нестандартной задачи, Такая задача может встретиться на уроке в школе, на занятии математического кружка, в журнале или книге. Решить такие задачи двумя вышеуказанными методами, порой, достаточно непросто. Поэтому существует еще один, позволяющий расширить диапазон способов математического моделирования и развития логического мышления у младших школьников, который называется геометрическим методом. Его особенностью, согласно Л. С. Луниной, является, в первую очередь, «…использование геометрических представлений (изображений), законов геометрии и элементов аналитических методов (уравнений, арифметических выражений и др.)» [2, с.4].
Приведем несколько примеров, способных расширить границы применения геометрического метода при решении текстовых задач в начальной школе.[2, с.3-10].
Пример 1. Задача на движение по прямой.
«Господин N вышел из пункта А по шоссе со скоростью 4 км/ч. На каком расстоянии от пункта А будет господин через 3 часа».
Существует несколько способов решения данной задачи.
I способ:
Решение в одно действие:
4 км/ч * 3 ч = 12 (км) – расстояние, которое пройдёт господин N через 3 часа со скоростью 4 км/ч.
II способ:
Решение с помощью построения графика на координатной плоскости:
1) На горизонтальной прямой отметим начало координат - т. О (назовём ось - Ох). На данной оси будем откладывать время движения господина N (единичный отрезок равен одному часу).
2) На вертикальной оси, проходящей через начало координат (ось Оу), будем откладывать расстояние, пройденное господином N (единичный отрезок равен одному часу).
3) За начало движения господина N берём точку О(0;0).
4) На оси Ох откладываем точку, координата которой равна 1 час. На оси Оу откладываем точку, координата которой равна 4 км. Точка В(1;4) показывает, что господин N за 1 час прошёл расстояние в 4 км.
5) Известно, что господин N движется по прямой (по шоссе). Через точку О(0;0) и точку В(1;4) проведём прямую. Данная прямая будет являться графиком движения господина N (Рис.1).
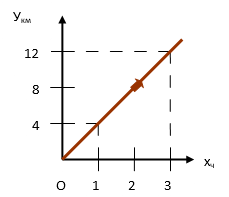
Рис.1
Пример 2. Задача на «движение вдогонку».
«Из пункта А со скоростью 6 км/ч вышел Петя. В том же направлении из пункта А спустя 3 часа выехал Вова на велосипеде со скоростью 12 км/ч. Через какое время Вова догонит Петю?»
Существует несколько способов решения данной задачи.
I способ: арифметический:
1) 6 км/ч *3 ч = 18 (км) – расстояние, которое прошёл Петя за 3 часа.
2) 12 км/ч – 6 км/ч = 6 (км/ч) – разница между скоростями Вовы и Пети.
3) 18 км :6 км/ч = 3 (ч) – время, через которое Вова догонит Петю.
Ответ: 3 часа.
II способ: решение с помощью построения графика на координатной плоскости:
1) На горизонтальной прямой отметим начало координат - т. О (назовём ось - Ох). На данной оси будем откладывать время движения мальчиков (единичный отрезок равен одному часу).
2) На вертикальной оси, проходящей через начало координат (ось Оу), будем откладывать расстояние, пройденное мальчиками (единичный отрезок равен одному часу).
3) За начало движения Вовы берём точку О(0;0). Отмечаем на графике точку D(1;6) – это означает, что за 1 час Вова пройдёт 6 км.
4) На оси Ох отмечаем точку А(3;0) - из этой точки будет строиться график движения Вовы, так как он выехал на 3 часа позже Пети.
5) Отмечаем на графике точку В(4;12) – эта точка означает, что через 1 час после движения Вовы прошло 4 часа от начала движения Вани; при этом Вова двигался со скоростью 12 км/ч.
6) Проводим прямую через точку А(3;0) и В(4;12) – график движения Вовы.
7) На графике находим точку, которая будет являться пересечением графиков движения – место, где Вова догонит Петю. Обозначим её буквой С(6;36). Это значит, что Вова догонит Петю на расстоянии 36 км от пункта А через 3 часа от начала своего движения. (Рис.2).
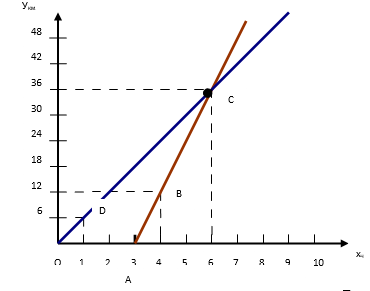
Рис.2
Пример №3. Задача на совместную работу.
«Бригада укладчиков плитки N может справиться с определённой работой за 7 недель. Через 2 недели после начала работы на помощь первой бригаде пришла вторая – бригада Р, которая может справиться с этой работой за 10 недель. За какое время обе бригады закончат работу?»
Существует несколько способов решения данной задачи.
I способ: арифметический:
Найдём время, за которое выполнит работу вторая бригада с учётом того, что первая бригада уже отработала 2 часа:
10 + 2 = 12 (нед.)
Найдём время, за которое обе бригады закончат работу:
12 – 7 = 5 (нед.)
Ответ: 5 недель.
II способ: решение с помощью построения графика на координатной плоскости:
- На горизонтальной прямой отметим начало координат - т. О (назовём ось - Ох). На данной оси будем откладывать время, за которое бригады выполнят работу (единичный отрезок равен 1 недели).
- На вертикальной оси, проходящей через начало координат (ось Оу), будем откладывать работу, которую необходимо выполнить (так как про данную величину информация не дана, то ставим на оси Оу произвольно точку О1 и проводим дополнительную ось времени - О1х1).
- Построим график работы бригады N. Для этого необходимо через точку, соответствующую 7 неделям, провести вертикальную прямую до пересечения с дополнительной осью времени – осью О1х1 (также её можно назвать осью завершения работы). Потом соединим точку О(0;0) и точку В(7;7) – точка пересечения осей. Полученная прямая будет являться графиком работы первой бригады.
- Построим график работы бригады Р. Для этого сначала нам необходимо предположить, что обеим бригадам надо выложить участок определённой длины. Первая бригада начала выкладывать плитку с одной стороны, а вторая – с противоположной. Так как бригады движутся навстречу друг другу, и вторая бригада начала свою работу позже на 2 недели, то график движения бригады Р мы начнём строить из точки А(2;7). Так как вторая бригада может выполнить задание за 10 недель и она начала свою работу через 2 недели после первой бригады, то точка, которая будет являться точкой окончания работы второй бригады, имеет координаты С(12;0).
- Буквой D(5;5) обозначим точку пересечения графиков работ двух бригад. Отсюда можно сделать вывод, что бригады закончат работу за 5 недель (Рис.3).
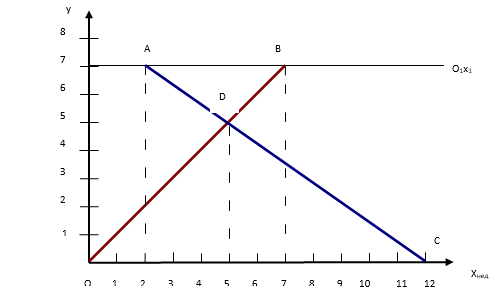
Рис.3
Подводя итоги всему вышесказанному, можно сделать вывод о том, что геометрический метод, наравне с арифметическим и алгебраическим, можно считать вполне целесообразным. Ведь он позволяет ученикам не только больше рассуждать над задачей, но и шире рассматривать законы математики, использовать геометрические представления и элементы аналитических методов уже на начальном этапе изучения математики. Согласно требованиям ФГОС НОО, чтобы обучение младших школьников было наиболее эффективным, необходимо использование при решении математической задачи максимального количества верных решений и их разнообразных записей, в том числе и геометрического метода, что является основой возможности предоставления ученикам выбора при обучении решению задачи.

 Р.
Ф. Швецова
Р.
Ф. Швецова