Проблема повышения познавательного интереса учащихся в процессе обучения занимает одно из ведущих мест в научных исследованиях.
В связи с внедрением ФГОС для учителей ставится новая цель «научить учить», для этого учителя сконцентрируются на личностном росте ученика. Важнейшим признаком личностного роста учеников играет познавательный интерес. Также многие исследователи, как М.Ф. Беляев, Я.И. Божович, Н.К. Крупская и др., считают, что познавательный интерес является главным аспектом обучения школьников.
Для более ясного обоснования нашей проблемы, особого внимания заслуживают труды Г.И.Щукиной, в которых подчеркнута значимость развития познавательного интереса как важнейшего образования личности в социальном возрасте, как самого энергичного стимулятора его деятельности.[3]
Рассматривая познавательный интерес как мотив учения, Г.И.Щукина отмечает, что он становится ценнейшим мотивом познавательной деятельности, в том случае, если школьник проявляет готовность, стремление совершенствовать свое учение. При этом познавательный интерес как мотив деятельности должен опираться на потребности самой личности, на то, что представляет для нее необходимость и ценность. [2]
Таким образом, Щукина выделяет следующие стадии развития познавательного интереса:
- любопытство;
- любознательность;
- познавательный интерес;
- устойчивый познавательный интерес. [2]
Мы думаем, что наиболее эффективным способом развития познавательного интереса является интегрированный урок, так как по мнению А.В. Багачука, Е.В. Фоменко, И.Е. Кизелевича интегрированные уроки должны отвечать следующим требованиям: во-первых, урок должен дать ребёнку самые различные знания, во-вторых, учитель должен повысить познавательный интерес школьников, в-третьих, урок должен активизировать мыслительную деятельность учащихся, и, наконец, дети должны проявлять творческие способности, ум. [1]
Исходя из теоретического анализа методической литературы, а также собственного опыта, в форме интегрированных уроков целесообразно проводить именно такие уроки, на которых будут раскрыты проблемы междисциплинарного характера. Проведение урока двумя или несколькими учителями с использованием различных интерактивных образовательных технологий позволяет разнообразить объём и уровень индивидуальной работы учащихся.
Чтобы лучше понять повышение познавательного интереса с помощью интегрированных уроков мы провели 9 уроков для учащихся 7 «а» класса.
Далее опишем методические особенности реализации интегрированного урока в процессе обучения математике учащихся 7 классов. Был проведен урок геометрии и черчении. Нами был выбран тип урока: урок «открытия» нового знания по теме «Окружность».
Цели урока:
Образовательные: Обеспечить усвоение понятия окружность и ее элементы, формировать навыки деления угла пополам, окружности на 4, 6, 8 равных частей.
Воспитательные: Содействовать формированию положительного отношения к урокам, понимания необходимых знаний, воспитания культуры поведения.
Развивающие: Показать, что знания, полученные при изучении одного предмета можно применять на уроках других предметов, развивать мышление, элементы творческой деятельности учащихся и умение контролировать свои действия.
На этапе «Мотивация к учебной деятельности», данный этап мы раскрыли тем, что каждый учитель взял на себя роль окружности и шара. Затем в стихотворной форме ставятся наводящие вопросы, такие как: Что такое шар? Что такое окружность? Что такое хорда? Что такое центр окружности? И так далее.
В следующем этапе «Актуализация знаний и фиксирование затруднения» мы переходим к нашей теме, также работаем с учебником Л.С. Атанасяна.
Далее был этап «Выявление места и причины затруднения». Это этап подведения к постановке проблемы. Задавались наводящие вопросы.
Далее был этап «Построение проекта выхода из затруднения». Для этого учащимся раздаются карточки. Карточки с 4 вариантами.
В-1 1. Прочитать п. 21 учебника; 2. Выписать в тетрадь основные термины новой темы. Записать на доске; 3. Выполнить устно № 143.
В-2 1. Прочитать п.21 учебника; 2. Ответить на вопрос 16 на стр.48.; 3. Выполнить устно № 143.
В-3 1. Прочитать п.21 учебника; 2. Выполнить устно №243 учебника; 3. Сравнить (найти общее и различие) понятия: а) радиус и хорда; б) круг и окружность.
В-4 1. Прочитать п.21 учебника; 2. Выполнить устно №143; 3. Придумать интересные вопросы к №143.
Затем на этапе «Первичное закрепление с внешним проговариванием» идет работа по учебнику «Черчение 7-9» А.Д. Ботвинникова §15.2 пункт «Деление окружности на четыре равные части»
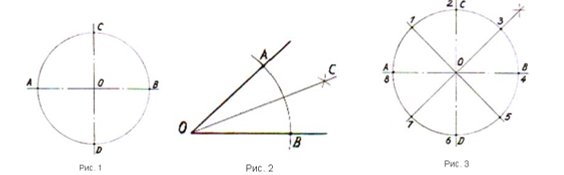
Выполнение построения окружности и деление ее на 4 равные части при помощи построения взаимно перпендикулярных диаметров, рис.1.
Построить хорды AD и BD, доказать, что они равны.
Построить хорды AC и BD, доказать, что они равны.
Вопрос: как разделить окружность на 8 равных частей? Из предложенных ответов выбрать деление угла пополам.
Деление угла пополам при помощи циркуля (объяснение учителя). Доказать <СОВ = <AОС. 1 человек у доски, остальные в тетрадях, “рис. 2”. Задание: разделить тупой, прямой углы пополам (2 человека у доски).
Деление окружности на 8 равных частей (используя способ деления угла пополам при помощи циркуля) рис. 3.
Затем идет этап «Самостоятельная работа с проверкой по эталону». Данный этап расположен на практическое применение геометрических построений. Задание: Деление окружности на 6 равных частей; работу выполнять на цветной бумаге.
На этапе «Рефлексия» было проведено анкетирование. Высказывание впечатлений об уроке учащимися.
И последний этап «Домашнее задание». По геометрии: № 144 в), 145. По черчению §15.2; стр. 101.
В течение урока, при выполнении построений помощь учащимся оказывают учитель математики, учитель черчения.
Таким образом, были проведены и другие интегрированные уроки. В начале и в конце были проведены диагностические процедуры. Мы воспользовались модифицированной диагностикой Г.И. Щукиной «Методика с конвертами». Результаты представлены в диаграмме №1. 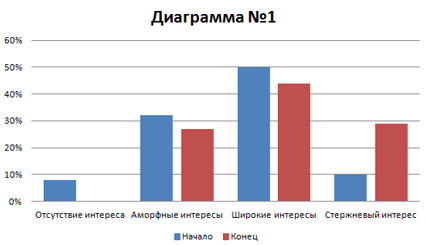
В заключении отметим, что опытно-экспериментальная работа, осуществляемая нами в естественных условиях образовательного процесса, убедила нас в перспективности реализации интегрированного урока в процессе обучения математики, так как нестандартные уроки вызывают интерес у учащихся и стремление, мотивация к учебному процессу.

 А.
Г. Иванова
А.
Г. Иванова