Полный текст статьи
Зыков Игорь Сергеевич,
студент факультета информатики, математики и физики ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров
Аннотация. Статья посвящена изучению открытых задач и возможностей их использования при обучении математике. В статье также рассматривается роль открытых задач как инструмента для развития творчества учащихся.
Ключевые слова: открытые задачи, технологии использования открытых задач, творчество, обучение математике.
Одним из важных направлений развития образования сегодня является преодоление репродуктивного стиля обучения и переход к такой образовательной системе, которая могла бы обеспечить познавательную активность и самостоятельность мышления учащихся. В связи с этим Федеральный государственный образовательный стандарт основного общего образования ориентирует школу не только на предметные, но и на метапредметные и личностные результаты, в том числе на обеспечение роста творческого потенциала учеников, их готовности к применению универсальных учебных действий в жизненных ситуациях [1].
Большинство сложившихся форм и методов обучения математике ориентированы на накопление учеником суммы знаний, а не на развитие его творческих способностей. Сегодня возникает острая необходимость формирования у школьника такой деятельности, которая позволяла бы ему полноценно сосуществовать с окружающей средой, а также творчески реализовывать себя в ней на основе своего внутреннего потенциала.
Будущее несет за собой огромный поток информации, с помощью которой человек ставит себе новые задачи и решает их. Подобную ситуацию можно сравнить с раздувающимся воздушным шаром. Воздух внутри его – это изученные факты, воздух вне шара – еще не изученная информация. А сама поверхность шара, как раз есть то, что на сегодняшний день является актуальной задачей. Чаще всего среди подобных задач встречаются не учебные задачи, а задачи, максимально приближенные к реальным жизненным ситуациям. Такими задачами являются открытые задачи [2].
Открытая задача может иметь неопределенное условие (с избыточными или недостаточными данными), разные пути решения, в открытой задаче присутствует неоднозначность решения.
Отсутствие заранее определенного решения, готового ответа стимулирует школьников к самопознанию, реализации своего творческого потенциала. Поначалу открытая задача может вызвать недоумение у учащихся. Лишь «сильные» учащиеся способны «окунуться с головой» в решение задачи. Это объясняется прежде всего разным уровнем индивидуального развития школьников, объема их мышления. Открытые задачи, по сравнению с задачами основного школьного курса или закрытыми, отличаются завышенной степенью неопределенности, с которой справиться может не каждый. Также можно выделить ту границу неопределенности задачи, дальше которой мозг учащегося справиться уже не может. Поэтому при построении системы открытых задач стоит уделять большое внимание такому требованию, как достаточность условия. Это требование будет поддерживать заинтересованность учащихся в решении задачи [3].
С другой стороны, важным фактором при использовании открытых задач в обучении является фактор времени. Все мы мыслим, исследуем и даже анализируем условие задачи на разном промежутке времени. Кому-то, чтобы понять суть задачи, путь к её решению и, непосредственно, решить её, понадобится 5 минут, а кто-то и до конца урока не сможет с ней разобраться. Чтобы несколько выровнять подобный временной разрыв, необходимо оказывать усиленную поддержку слабым ученикам, в то время как сильные будут приучаться к самостоятельности в решении открытых задач, но не следует забывать и про них.
Многие школьные задачи можно переформулировать в открытые задачи. Для этого достаточно, например, переформулировать вопрос задачи [4].
Рассмотрим задачу из школьного курса геометрии 7-го класса.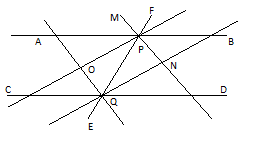
Решение. Так как сумма углов APQ и CQP равна 180º, то AB || CD по третьему признаку параллельности прямых. угол MPO равен полусумме углов APQ и APF, то есть равен 90º. Сумма углов OPQ и OQP также равна 90º, поскольку полусумма углов CQP и APQ равна 90º. Сумма углов OPQ и QPN равна 90º, так как сумма этих углов – угол, смежный с MPO. Следовательно, углы OQP и QPN равны. А это накрест лежащие углы при прямых AQ и MN и секущей EF. Следовательно, AQ || MN по первому признаку параллельности прямых.
Преобразовать задачу можно следующим образом.
Задача 1а. Две прямые AB и CD пересечены третьей прямой EF. Сумма односторонних углов при их пересечении равна 180º. AQ и MN – биссектрисы. Что можно сказать про прямые AB и CD, AQ и MN? Какой вид имеет четырехугольник OPNQ? Что нужно убрать из условия, чтобы четырехугольник OPNQ стал параллелограммом?
Предполагаемое решение. Параллельность прямых AB и CD, AQ и MN доказана выше. Так как углы OPN и QNP по 90°, то OPNQ – прямоугольник. Для того, чтобы OPNQ стал параллелограммом достаточно убрать из условия тот факт, что AQ и MN – биссектрисы.
При обучении математике можно выделить две стратегии в последовательности использования открытых и закрытых задач.
1. Прямая последовательность традиционного обучения: отрабатывать отдельные навыки с помощью закрытых задач и учиться использовать эти навыки в жизни с помощью открытых.
2. Обратная последовательность проблемного обучения: вводить материал с помощью открытых задач и доводить до автоматизма отдельные навыки с помощью закрытых.
Поскольку открытые задачи можно отнести к задачам, максимально приближенным к реальным, то решение таких задач приводит к приближению школы к жизни. То есть на примере решения открытых задач учащийся тренируется перед решением будущих проблем, возникающих в жизни. Но нельзя забывать и про закрытые задачи. Ведь решение таких задач даёт тот базис для решения более сложных, запутанных жизненных ситуаций, формируют те элементарные навыки, необходимые в жизни.
Следуя первой стратегии, бывает малоэффективно и даже часто вредно давать ученикам отдельные способы решения задач без того, чтобы поставить ученика в такую, вполне реалистичную, но учебную проблемную ситуацию, решение которой как раз и требует применения изучаемого метода.
Представьте себе ребенка, который не умеет чистить зубы, умываться, одеваться. Такой ребенок будет получать насмешки, что приведет к его эмоциональному дискомфорту. При самостоятельном овладении ребенок потратил бы на обучение несравнимо большее время, чем при целенаправленном обучении с помощью закрытых задач, когда заботливые родители изначально четко определяют цели, задачи, способы действия. Кроме того, ребенок теоретически имеет возможность неоднократно пробовать, ошибаться и снова пробовать, продираясь сквозь чащу неопределенностей этих открытых жизненных задач. Но насколько драматичней становится ситуация, если ребенок методом «проб и ошибок» учился бы, например, правилам дорожного движения.
С другой стороны, попытка использовать открытые задачи на стадии ознакомления с новым материалом связана с очевидной сложностью – это требует методической переработки всего учебного курса. Именно поэтому более эффективной представляется смешанный вариант, при котором открытые задачи используются как при введении нового материала, так и на стадии отработки полученных знаний. На стадии отработки технологически достаточно легко использовать разные типы открытых задач, но это не избавляет от проблемы специальной их разработки.
Таким образом, одним из главных путей развития продуктивного мышления является открытие новых знаний через решение специально подобранных открытых задач, а освоение всей его полноты и закрепление как с помощью традиционных школьных закрытых задач, так и различного рода открытых.
Ссылки на источники
1. Федеральный государственный образовательный стандарт основного общего образования. – М.: Госстандарт России: Изд-во стандартов.
2. Горев П. М., Утёмов В. В. Формула творчества: Решаем открытые задачи. Материалы эвристической олимпиады «Совёнок». – Киров: Изд-во ВятГГУ, 2011. – 288 с.
3. Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: прикладной курс научного творчества. – Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с.
4. Горев П. М., Сорокина А. В. Признаки равенства треугольников как задача открытого типа при изучении геометрии в основной школе // Концепт. – 2012. – № 6 (июнь). – ART 12065. – URL: http://e-koncept.ru/2012/12065.htm.
студент факультета информатики, математики и физики ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров
Аннотация. Статья посвящена изучению открытых задач и возможностей их использования при обучении математике. В статье также рассматривается роль открытых задач как инструмента для развития творчества учащихся.
Ключевые слова: открытые задачи, технологии использования открытых задач, творчество, обучение математике.
Одним из важных направлений развития образования сегодня является преодоление репродуктивного стиля обучения и переход к такой образовательной системе, которая могла бы обеспечить познавательную активность и самостоятельность мышления учащихся. В связи с этим Федеральный государственный образовательный стандарт основного общего образования ориентирует школу не только на предметные, но и на метапредметные и личностные результаты, в том числе на обеспечение роста творческого потенциала учеников, их готовности к применению универсальных учебных действий в жизненных ситуациях [1].
Большинство сложившихся форм и методов обучения математике ориентированы на накопление учеником суммы знаний, а не на развитие его творческих способностей. Сегодня возникает острая необходимость формирования у школьника такой деятельности, которая позволяла бы ему полноценно сосуществовать с окружающей средой, а также творчески реализовывать себя в ней на основе своего внутреннего потенциала.
Будущее несет за собой огромный поток информации, с помощью которой человек ставит себе новые задачи и решает их. Подобную ситуацию можно сравнить с раздувающимся воздушным шаром. Воздух внутри его – это изученные факты, воздух вне шара – еще не изученная информация. А сама поверхность шара, как раз есть то, что на сегодняшний день является актуальной задачей. Чаще всего среди подобных задач встречаются не учебные задачи, а задачи, максимально приближенные к реальным жизненным ситуациям. Такими задачами являются открытые задачи [2].
Открытая задача может иметь неопределенное условие (с избыточными или недостаточными данными), разные пути решения, в открытой задаче присутствует неоднозначность решения.
Отсутствие заранее определенного решения, готового ответа стимулирует школьников к самопознанию, реализации своего творческого потенциала. Поначалу открытая задача может вызвать недоумение у учащихся. Лишь «сильные» учащиеся способны «окунуться с головой» в решение задачи. Это объясняется прежде всего разным уровнем индивидуального развития школьников, объема их мышления. Открытые задачи, по сравнению с задачами основного школьного курса или закрытыми, отличаются завышенной степенью неопределенности, с которой справиться может не каждый. Также можно выделить ту границу неопределенности задачи, дальше которой мозг учащегося справиться уже не может. Поэтому при построении системы открытых задач стоит уделять большое внимание такому требованию, как достаточность условия. Это требование будет поддерживать заинтересованность учащихся в решении задачи [3].
С другой стороны, важным фактором при использовании открытых задач в обучении является фактор времени. Все мы мыслим, исследуем и даже анализируем условие задачи на разном промежутке времени. Кому-то, чтобы понять суть задачи, путь к её решению и, непосредственно, решить её, понадобится 5 минут, а кто-то и до конца урока не сможет с ней разобраться. Чтобы несколько выровнять подобный временной разрыв, необходимо оказывать усиленную поддержку слабым ученикам, в то время как сильные будут приучаться к самостоятельности в решении открытых задач, но не следует забывать и про них.
Многие школьные задачи можно переформулировать в открытые задачи. Для этого достаточно, например, переформулировать вопрос задачи [4].
Рассмотрим задачу из школьного курса геометрии 7-го класса.

Рис. 1
Задача 1. Две прямые AB и CD пересечены третьей прямой EF (рис. 1). Сумма односторонних углов при их пересечении равна 180º. AQ и MN – биссектрисы. Доказать, что прямые AB и CD, AQ и MN параллельны?Решение. Так как сумма углов APQ и CQP равна 180º, то AB || CD по третьему признаку параллельности прямых. угол MPO равен полусумме углов APQ и APF, то есть равен 90º. Сумма углов OPQ и OQP также равна 90º, поскольку полусумма углов CQP и APQ равна 90º. Сумма углов OPQ и QPN равна 90º, так как сумма этих углов – угол, смежный с MPO. Следовательно, углы OQP и QPN равны. А это накрест лежащие углы при прямых AQ и MN и секущей EF. Следовательно, AQ || MN по первому признаку параллельности прямых.
Преобразовать задачу можно следующим образом.
Задача 1а. Две прямые AB и CD пересечены третьей прямой EF. Сумма односторонних углов при их пересечении равна 180º. AQ и MN – биссектрисы. Что можно сказать про прямые AB и CD, AQ и MN? Какой вид имеет четырехугольник OPNQ? Что нужно убрать из условия, чтобы четырехугольник OPNQ стал параллелограммом?
Предполагаемое решение. Параллельность прямых AB и CD, AQ и MN доказана выше. Так как углы OPN и QNP по 90°, то OPNQ – прямоугольник. Для того, чтобы OPNQ стал параллелограммом достаточно убрать из условия тот факт, что AQ и MN – биссектрисы.
При обучении математике можно выделить две стратегии в последовательности использования открытых и закрытых задач.
1. Прямая последовательность традиционного обучения: отрабатывать отдельные навыки с помощью закрытых задач и учиться использовать эти навыки в жизни с помощью открытых.
2. Обратная последовательность проблемного обучения: вводить материал с помощью открытых задач и доводить до автоматизма отдельные навыки с помощью закрытых.
Поскольку открытые задачи можно отнести к задачам, максимально приближенным к реальным, то решение таких задач приводит к приближению школы к жизни. То есть на примере решения открытых задач учащийся тренируется перед решением будущих проблем, возникающих в жизни. Но нельзя забывать и про закрытые задачи. Ведь решение таких задач даёт тот базис для решения более сложных, запутанных жизненных ситуаций, формируют те элементарные навыки, необходимые в жизни.
Следуя первой стратегии, бывает малоэффективно и даже часто вредно давать ученикам отдельные способы решения задач без того, чтобы поставить ученика в такую, вполне реалистичную, но учебную проблемную ситуацию, решение которой как раз и требует применения изучаемого метода.
Представьте себе ребенка, который не умеет чистить зубы, умываться, одеваться. Такой ребенок будет получать насмешки, что приведет к его эмоциональному дискомфорту. При самостоятельном овладении ребенок потратил бы на обучение несравнимо большее время, чем при целенаправленном обучении с помощью закрытых задач, когда заботливые родители изначально четко определяют цели, задачи, способы действия. Кроме того, ребенок теоретически имеет возможность неоднократно пробовать, ошибаться и снова пробовать, продираясь сквозь чащу неопределенностей этих открытых жизненных задач. Но насколько драматичней становится ситуация, если ребенок методом «проб и ошибок» учился бы, например, правилам дорожного движения.
С другой стороны, попытка использовать открытые задачи на стадии ознакомления с новым материалом связана с очевидной сложностью – это требует методической переработки всего учебного курса. Именно поэтому более эффективной представляется смешанный вариант, при котором открытые задачи используются как при введении нового материала, так и на стадии отработки полученных знаний. На стадии отработки технологически достаточно легко использовать разные типы открытых задач, но это не избавляет от проблемы специальной их разработки.
Таким образом, одним из главных путей развития продуктивного мышления является открытие новых знаний через решение специально подобранных открытых задач, а освоение всей его полноты и закрепление как с помощью традиционных школьных закрытых задач, так и различного рода открытых.
Ссылки на источники
1. Федеральный государственный образовательный стандарт основного общего образования. – М.: Госстандарт России: Изд-во стандартов.
2. Горев П. М., Утёмов В. В. Формула творчества: Решаем открытые задачи. Материалы эвристической олимпиады «Совёнок». – Киров: Изд-во ВятГГУ, 2011. – 288 с.
3. Утёмов В. В., Зиновкина М. М., Горев П. М. Педагогика креативности: прикладной курс научного творчества. – Киров: АНОО «Межрегиональный ЦИТО», 2013. – 212 с.
4. Горев П. М., Сорокина А. В. Признаки равенства треугольников как задача открытого типа при изучении геометрии в основной школе // Концепт. – 2012. – № 6 (июнь). – ART 12065. – URL: http://e-koncept.ru/2012/12065.htm.

 И.
С. Зыков
И.
С. Зыков