Аннотация. В статье сформулирован критерий для классификации критических точек на три типа (симметричная, асимметричная точка бифуркации и предельная точка) и предложен аналитический анализ чувствительности трех типов некратной критической нагрузки и перемещений конструкции. Для анализа чувствительности применяются прямой и сопряженный методы. Искомые производные необходимы в задачах оптимизации с ограничениями на критическую нагрузку потери устойчивости конструкции, где используются аппроксимации активных ограничений. Дополнительным ограничением в рассматриваемой задаче оптимизации является условие возникновения точек бифуркации раньше предельных точек. Приводятся примеры оптимального проектирования ферм с некратными симметричными, асимметричными точками бифуркации и предельными точками.
Ключевые слова: оптимизация, аналитический анализ чувствительности, геометрически нелинейные конструкции, критическая сила общей потери устойчивости, некратные предельные точки, некратные симметричные и асимметричные точки бифуркации.
Рассматривается геометрически нелинейная упругая конструкция. Считается априори, что для достаточно малых значений внешней консервативной нагрузки равновесие конструкции устойчиво. При дальнейшем нагружении у конструкции наступает критическое состояние, при котором касательная матрица жесткости становится особенной. В работе приведен критерий для классификации особых состояний – некратные симметричная или асимметричная точка бифуркации, или предельная точка. Поэтому важными оказываются две задачи: мгновенное поведение конструкции после критической точки и изменение критической нагрузки потери устойчивости в зависимости от варьируемых параметров. В данной работе рассматриваются случаи, когда при варьировании параметров конструкции значение критической нагрузки изменяется, а тип критической точки не изменяется. В некоторых случаях варьирование параметров конструкции или геометрические несовершенства могут вызывать изменение типа критической точки или исчезновение критической точки. Такие случаи здесь не рассматриваются. Данное исследование придерживается работ [1–8] по анализу чувствительности критической нагрузки потери устойчивости и частот собственных колебаний пластин, оболочек, плоских ферм.
Выводятся явные выражения для производных критического множителя нагрузки и перемещений для некратной симметричной, асимметричной точки бифуркации и предельной точки. Далее ставится задача оптимизации геометрически нелинейных конструкций с ограничениями на некратную критическую нагрузку потери устойчивости, принимая во внимание, что точка бифуркации возникает раньше предельной точки.
2. Постановка задачи оптимизации







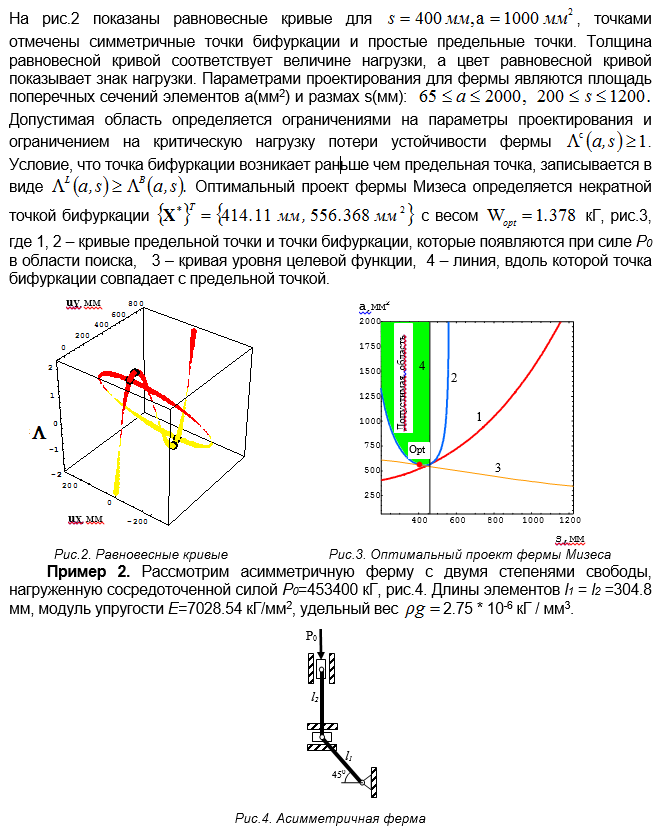
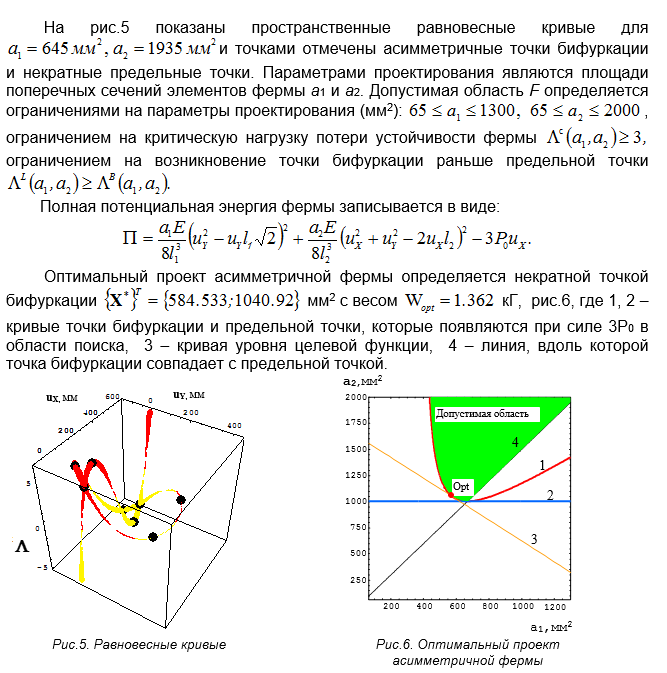
Заключение
В статье выполняется аналитический анализ чувствительности трех типов некратной критической нагрузки потери устойчивости конструкции и перемещений. Для анализа чувствительности применяются прямой и сопряженный методы. Впервые формулируется критерий для обнаружения ассимметричной точки бифуркации. Приводятся примеры оптимизации ферм с некратными симметричными и асимметричными точками бифуркации и предельными точками.
Ссылки на источники:
1. Сергеев, О. А. Оптимизация геометрически нелинейных пространственных рам с учетом ограничений по прочности и общей устойчивости / О. А. Сергеев, В. Г. Киселев, С. А. Сергеева // Проблемы прочности и пластичности: Межвуз. сб. / Н.Новгород: Изд-во ННГУ. – 2001. – Вып. 63. – С. 111–118.
2. Сергеев, О. А. Анализ чувствительности и оптимальное проектирование геометрически нелинейных рам с учетом общей потери устойчивости / О. А. Сергеев, С. А. Сергеева, В. Г. Киселев // Вестник ННГУ. Серия механика / Н.Новгород: Изд-во ННГУ. – 2002. – Вып. 1(4). – С. 161–175.
3. Sergeyev, O. A. Optimization of 3D frame structures for stress and overall stability constraints / O. A. Sergeyev, S. A. Sergeyeva, V. G. Kiselev // Proceedings of the 4-th world congress of structural and multidisciplinary optimization.– Dalian, China. – 2001. P. 79–80.
4. Bojczuk, D. Non-linear sensitivity analysis of discrete structures / D. Bojczuk, Z. Mróz // Foundations of civil and environmental engineering. – 2002. – 1. – P. 19–41.
5. Mróz, Z. Sensitivity analysis and optimal design of nonlinear structures / Z. Mróz, J. Piekarski // Int. J. Numer. Meth. Engng. – 1998. – 42. – P. 1231–1262.
6. Mróz, Z., Haftka, R.T. Design Sensitivity Analysis of Non-Linear Structures in Regular and Critical States. Int. J. Solids Struc., 1994, 31, 2071-2098.
7. Сергеев, О. А. Анализ закритического поведения геометрически нелинейных упругих пространственных рам / О. А. Сергеев, В. Г. Киселев // Вестник ННГУ. Серия механика / Н.Новгород: Изд-во ННГУ. – 2004. – Вып. 1(6). – С. 177–190.
8. Сергеев, О. А. Анализ устойчивости равновесных кривых нелинейных конструкций и анализ чувствительности в кратных критических точках / О. А. Сергеев, В. Г. Киселев // Проблемы прочности и пластичности: Межвуз. сб. / Н.Новгород: Изд-во ННГУ. – 2006. – Вып. 68. – С. 126–138.
Sergeyev O.A.
Senior scientist of Engineering company “Express plus”
Kiselev V.G.
Associate Professor of Department of computer information systems of financial calculations Lobachevsky State University of Nizhni Novgorod
Sergeyeva S.A.
Associate Professor of department of aero-hydrodynamics, strength of machines and materials, faculty of marine and aviation equipment, Nizhny Novgorod state technical University n.a. Р.Е. Alekseev, Novgorod
Sensitivity analysis in non-multiple critical points and optimal design of geometrically nonlinear structures
Abstract. The article presents the criterion for the classification of critical points in three types (symmetric, asymmetric bifurcation point and limit point) and the analytical sensitivity analysis of the three types of non-multiple overall buckling load and displacements is introduced. For sensitivity analysis direct and adjoint methods are applied. The required derivatives are needed in optimization problems with constraints on the buckling load of the structure. The approximations of the active constraints are used. Additional constraint in the considered problem of optimization is the condition for the occurrence of bifurcation points earlier limit points. The examples of optimal design of trusses with nonmultiple symmetric, asymmetric bifurcation points and limit points are considered.
Keywords: optimization, analytical sensitivity analysis of geometrically nonlinear structures, overall buckling load, non-multiple limit points, non-multiple symmetric and asymmetric bifurcation points.

 О.
А. Сергеев
О.
А. Сергеев