«Пик интереса» учащегося к математике приходится на 11-13 лет, и задача заключается в том, чтобы пробудить его, развить, удержать. Стремление к самопознанию и самовоспитанию у пятиклассников выше, чем у остальных у остальных школьников. Так как в этом возрасте быстро развивается логическая память, формируется произвольное внимание. Поэтому приходится искать новые формы работы. Одной из таких форм является курс «Трудовая деятельность в задачах».
Курс «Трудовая деятельность в задачах» дает возможность активизировать познавательную деятельность учащихся, как на уроках математики, так и во внеклассной работе. Решение задач помогает развить потенциальные возможности учащихся, прививает интерес к предмету, учит не только находить пути решения этих задач, а также формирует у учащихся способности к самостоятельному творческому мышлению и творческой активности. Учащиеся учатся находить решения и способы решения. Сегодня – математические, завтра – профессиональные и жизненные. Настоящий курс для 5 класса позволяет привлечь не только учащихся, проявивших интерес к математике, но и тех, которые еще не осознали своих способностей. Разнообразие задач, которые, естественно, не все могут найти отражение в школьном курсе, но которыми так богата математика, должны быть достоянием не только сильных учащихся.
Основными формами организации учебно-познавательной деятельности учащихся являются: изложение узловых вопросов данного факультативного курса (лекционный метод), собеседования (дискуссии), тематическое комбинированное занятие, соревнование, решение задач, доклады учащихся. Акцент на занятиях курса сделан на самостоятельную работу учащихся. Уделяется больше внимания индивидуальной работе учащихся и меньше – фронтальной работе. В этой статье предлагается содержание занятия курса по теме «Проценты».
Цель занятия: сформировать у учащихся представление о возможностях широкого использования процентов в реальных жизненных ситуациях.
Задачи занятия:
- ознакомление учащихся с основными понятиями и методами решения задач на проценты;
- формирование устойчивого интереса школьников к предмету в ходе получения ими дополнительной информации;
- повышение уровня математического развития школьников в результате углубления и систематизации их знаний по основному курсу
Введение. Слово «процент» происходит от латинских слов pro centum, что буквально означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотых долях. Это дает возможность упрощать расчеты и легко сравнивать части между собой и с целым. Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян, которые пользовались шестидесятеричными дробями. Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Ныне процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу).
В нашей стране ими пользуются при составлении и учете выполнения производственных планов в промышленности и сельском хозяйстве при разных денежных расчетах.
Вспомним, как выражать десятичную дробь в процентах и процент представлять в виде десятичной дроби.
1. Правила.
1. Чтобы обратить десятичную дробь в проценты, надо ее умножить на 100 и добавить знак %.
2. Чтобы перевести проценты в десятичную дробь, надо убрать знак % и разделить число на 100.
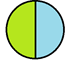
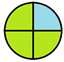
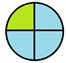
Для того чтобы облегчить решение многих задач, учащимся предлагается создать универсальную таблицу перевода дробей в проценты.
Пример 1. Заполните недостающие данные в таблице (таблица 1).
Таблица 1
|
Картинка |
|
|
|
|
|
|
|
|
|
|
Дробь |
1/2 |
|
|
1/5 |
|
|
1/10 |
|
|
|
Десятичная дробь |
|
0,25 |
|
|
0,4 |
|
|
0,05 |
|
|
Процент |
|
|
75 % |
|
|
60% |
|
|
2% |
Решение. Заполним 2,3 и 4 столбики.
2 столбик:
½ = 0,5
0,5 = 0,5 ∙ 100% = 50 %
3 столбик:
0,25 = 25 : 100 = ¼
0,25 = 0,25 ∙ 100% = 25 %
4 столбик:
75% = 75 : 100 = 0,75
0,75 = 75 : 100 = ¾
Остальные столбики заполняются аналогично. После всех вычислений должна получиться таблица 2.
Таблица 2
|
Картинка |
 |
 |
 |
|
|
|
|
|
|
|
Дробь |
1/2 |
1/4 |
3/4 |
1/5 |
2/5 |
3/5 |
1/10 |
1/20 |
1/50 |
|
Десятичная дробь |
0,5 |
0,25 |
0,75 |
0,2 |
0,4 |
0,6 |
0,1 |
0,05 |
0,02 |
|
Процент |
50% |
25% |
75% |
20% |
40% |
60% |
10% |
5% |
2% |
Покажем, как работают правила перевода на конкретных примерах. Решаем вместе с учениками.
Пример 2. Петр Иванович собирается купить через Интернет стиральную машину, пароварку и пылесос. Он изучает цены и сравнивает доставки в трёх фирмах. Цены товара и условия доставки приведены в таблице (таблица 3). Какова стоимость самого дешевого варианта покупки?
Таблица 3
|
Магазин |
Цена стиральной машины (руб.) |
Цена пылесоса (руб.) |
Цена пароварки (руб.) |
Доставка (руб.) |
Дополнительные условия |
|
I |
13500 |
4000 |
2800 |
1000 |
При общей стоимости товара более 20000руб. пароварка в подарок |
|
II |
14200 |
4500 |
3200 |
500 |
При общей стоимости товара более 20000руб. дается скидка на товар 10% |
|
III |
11800 |
3800 |
2500 |
1000 |
При общей стоимости товара более 15000руб. доставка бесплатно |
Решение.
1) 13500 + 4000 + 2800 = 20300 руб. > 20000 руб. Значит, пароварка в подарок.
20300 – 2800 + 1000 = 18500 руб. стоимость покупки с учетом доставки.
2) 14200 + 4500 + 3200 = 21900 руб. > 20000 руб. Дается скидка на товар 10 %.
10 % = 10 : 100 = 0,1
21900 – 21900 + 500 = 20210 руб. Стоимость покупки с учетом скидки и доставки.
3) 11800 + 3800 ∙ 0,1 + 2500 = 18100 руб. > 15000 руб. Значит, доставка бесплатно.
Ответ: стоимость самого дешевого варианта покупки составляет 18100 руб.
Пример 3. Монтаж водостоков в доме берутся выполнить три бригады. Стоимость работы, материалов и транспортные расходы приведены в таблице (таблица 4). При этом III бригада выполняет работу под «ключ», за срочное выполнение работы требует 4 % премиальных от исходной цены. Какова цена самого дешевого варианта?
Таблица 4
|
Бригада |
Стоимость работы (руб.) |
Стоимость материала (руб.) |
Транспортные расходы (руб.) |
Дополнительные условия |
|
I |
7000 |
11200 |
2500 |
- |
|
II |
8500 |
9500 |
3000 |
- |
|
III |
20000 |
- |
- |
4 % от стоимости |
Решение.
1) 7000 + 11200 + 2500 = 20700 руб.
2) 8500 + 9500 + 3000 = 21000 руб.
3) 4% = 4 : 100 = 0,04
20000 + 20000 ∙ 0,04 = 20800 руб.
Ответ: стоимость самого дешевого варианта составляет 20700 руб.
Пример 4. Розничная цена учебника 354 руб., она на 18 % выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 7000 руб.?
Решение. Пусть х руб. – цена оптового учебника, тогда 354 это 118 %∙х – это 100 %. Находим х:
1) х = 354 ∙ 100 : 118 = 300 руб.
2) 7000 : 300 = 23 учебника
Ответ: 23 учебника.
Пример 5. Железнодорожный билет для взрослого стоит 590 рублей. Стоимость билета школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 14 школьников и 3 взрослых. Сколько стоят билеты на всю группу?
Решение. 1 способ.
1) 590 ∙ 50 : 100 = 295 руб. стоит билет для школьника
2) 14 ∙ 295 + 3 ∙ 590 = 5900 руб.
2 способ. Т.к. стоимость билета школьника составляет 50% от стоимости билета для взрослого, то 1 билет для взрослого равен 2 билетам для школьника. Значит, стоимость 14 билетов для школьников равна стоимости 7 билетов для взрослых. Получается 7 + 3 = 10 взрослых билетов. 10 ∙ 590 = 5900 руб. стоят билеты на всю группу.
Ответ: 5900 руб.
Пример 6. Магазин закупает цветочные горшки по оптовой цене 130 руб. за штуку. Торговая наценка составляет 15 %. Какое наибольшее число таких горшков можно купить в этом магазине на 1100 рублей?
Решение. 1) 100 % + 15% = 115 % – цена горшка для продажи в процентах
115 % = 1,15
2) 130 ∙ 1,15 = 149,5 руб. – цена одного горшка для продажи
3) 1100 : 149,5 = 7 горшков и 53,5 руб. сдача.
Ответ: 7 горшков.
2. Задачи для самостоятельного решения в классе.
Пример 7. Спортивный лагерь еженедельно закупает с фермы молоко и сметану в количестве 300л молока и 20кг сметаны. Поставщиком могут быть три различные фермы. Цены на продукты и транспортные расходы приведены в таблице (таблица 5). Какова стоимость самого дешевого варианта?
Таблица 5
|
Ферма |
Стоимость 1л молока (руб.) |
Стоимость 1кг сметаны (руб.) |
Транспортные расходы (руб.) |
Дополнительные условия |
|
I |
8,5 |
120 |
1500 |
При общей стоимости покупки более 5000руб. доставка бесплатно |
|
II |
7 |
110 |
2000 |
При общей стоимости покупки более 4000руб. стоимость доставки снижается на 40% |
|
III |
6,5 |
100 |
2000 |
- |
Решение.
1) 300 ∙ 8,5 + 20 ∙ 120 = 4950 руб. < 5000 руб.
4950 + 1500 = 6450 руб.
2) 300 ∙ 7 + 20 ∙ 110 = 4300 руб. > 4000 руб.
100% – 40% = 60%
4300 + 2000 ∙ 0,6 = 5500 руб.
3) 300 ∙ 6,5 + 20 ∙ 100 + 2000 = 5950 руб.
Ответ: 5500 руб.
Пример 8. После снижения цен на ткань на 15 % 1 м ткани стали продавать на 75 руб. дешевле. Сколько стоил 1м этой ткани до снижения?
Решение. 75 : 0,15 = 500 руб.
Ответ: 500 руб.
Пример 9. На соревнованиях авиамоделистов первая модель пролетела на 10 %, или на 480 м, меньше второй. Скорость первой модели на 20 %, или на 1 м в секунду, больше скорости второй модели. Сколько времени находилась в воздухе каждая модель?
Решение. Пусть х метров пролетела вторая модель, тогда первая модель пролетела (х – 480) или 0,9 ∙ х метров.
1) 480 : 10 ∙ 100 = 4800 м пролетела вторая модель
4800 ∙ 0,9 = 4320 м пролетела первая модель
2) 1 ∙ 0,2 = 5 м/с скорость второй модели
5 + 1 = 6 м/с скорость первой модели
3) 4320 : 6 = 720 с. находилась в воздухе первая модель
4800 : 5 = 960 с. находилась в воздухе вторая модель
Ответ: 720с. находилась в воздухе первая модель, 960 с. находилась в воздухе вторая модель.
Пример 10. В первую половину дня два тракториста вспахали вместе 16,2 га, причем первый вспахал на 1,8 га больше второго и каждый выполнил по 60 % взятого обязательства. Какую площадь должен вспахать каждый тракторист?
Решение. Пусть х га вспахал второй тракторист, тогда (1,8 + х) вспахал первый.
1) х + х + 1,8 = 16,2
х = 7,2 га вспахал первый тракторист
7,2 + 1,8 = 9 га вспахал второй тракторист
2) 7,2 : 0,6 = 12 га должен вспахать первый тракторист
9 : 0,6 = 15 га должен вспахать второй тракторист
Ответ: 12 га должен вспахать первый тракторист, 15 га должен вспахать второй тракторист.
Пример 11. Цена на электрический чайник была повышена на 21 % и составила 2420 руб. Сколько рублей стоил чайник до повышения цены?
Решение. 100 % + 21 % = 121 % = 1,21
2420 : 1,21 = 2000 руб.
Ответ: 2000 руб. стоил чайник до повышения цены.
Пример 12. Розничная цена учебника 345 руб., она на 15 % выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 5000 рублей?
Решение.
1) 100% + 15 % = 115% = 1,15
345 : 1,15 = 300 руб. оптовая цена учебника.
2) 5000 : 300 = 16 уч. ( сдача 200 руб.)
Ответ: 16 учебников.
3. Задачи для самостоятельного решения дома.
1. Магазин закупает цветочные горшки по оптовой цене 140 руб. за штуку. Торговая наценка составляет 20 %. Какое наибольшее число таких горшков можно купить в этом магазине на 1110 рублей?
2. Цена на электрический чайник была повышена на 22 % и составила 3050 руб. Сколько рублей стоил чайник до повышения цены?
3. Уставный фонд товарищества составлял 100000 руб. Доля каждого участника равна 10% уставного фонда. Сколько участников в этом товариществе?
4. Номинальная заработная плата составляет 22843 руб. Из нее высчитывается 13% налогов. Сколько денег останется у работника после уплаты налогов?
5. Предприятие взяло 1000000 руб. в банке в кредит на 6 месяцев под 24 % годовых. Сколько денег должно отдать предприятие банку через полгода?
6. Инфляция в декабре снизилась до 12 % по сравнению с 16 % в ноябре. Сколько стали «стоить» 1000 руб. в декабре?

 Л.
В. Турышева
Л.
В. Турышева