В современном мире требования к ученику как к личности возрастают. Они должны уметь решать проблемы разного уровня самостоятельно. Поэтому проблемное обучение является одной из самых важных сторон подготовки школьников. Проблемное обучение развивает самостоятельность учеников и формирует навыки учебно-исследовательской деятельности.
В настоящее время в связи с внедрением в образовательный процесс Федеральных Государственных образовательных стандартов проблемное обучение является одним из эффективнейших процессов обучения, так как оно направлено на развитие личности ребенка, на самостоятельную добычу знаний и умений.
При рассмотрении теоретических основ проблемного обучения школьников, на основании трудов Мирзы Исмаиловича Махмутова было выделено наиболее обобщенное определение понятия проблемного обучения: проблемное обучение - это тип развивающего обучения, в котором сочетается систематическая самостоятельная поисковая деятельность учащихся с усвоением ими готовых выводов науки, а система методов построена с учетом целеполагания и принципа проблемности. [3, с.267]
Основными понятиями проблемного обучения являются "проблемная ситуация" и "учебная проблема".
По определению Л.П. Русиновой: учебная проблема – это практическая или теоретическая трудность, решение которой является результатом собственной исследовательской активности ученика. Фоном этой трудности обычно бывает целесообразно организованная ситуация, в которой ученик, руководствуясь определенными потребностями, стремится к преодолению трудности и добывает таким образом новые знания и новый опыт. В каждой настоящей учебной проблеме должно быть что-то неизвестное. [4]
По определению А.М. Матюшкина проблемная ситуация – это особый вид мыслительного взаимодействия субъекта и объекта; характеризуется таким психическим состоянием, возникающим у субъекта (учащегося) при выполнении им задания. Которое требует найти новые, ранее не известные субъекту знания или способы действия. [2, с. 193]
Приведем пример плана урока геометрии в 7 классе по учебнику Л.С. Атанасяна, В.Ф. Бутузова и др. по теме: «Неравенство треугольника» с использованием проблемной ситуации с затруднением.
Цель темы: изучить теорему о неравенстве треугольника и показать ее применение при решении задач.
Тип урока: урок изучения нового материала
Учебник: Атанасян Л.С., Бутузов В.Ф. и др., «Геометрия» 7-9 класс
Оборудование: учебник, мел, доска.
УУД:
- личностные: формировать позицию школьника на уровне положительного отношения к школе, друг к другу;
- регулятивные: учить применять и сохранять учебную задачу, учить решать задачи с использованием теоремы о неравенстве треугольника;
- познавательные: познакомить детей с теоремой о неравенстве треугольника, закрепить первичные навыки по данной теме;
- коммуникативные: выходить из проблемной ситуации, решая ее друг с другом, использовать речевые средства для эффективного решения задач.
Форма организации познавательной деятельности:
1). Индивидуально-развивающее обучение.
Структура урока:
1). Орг. Момент. (1 мин)
2). Актуализация знаний. (3 мин)
3). Постановка проблемной ситуации. Формулирование учебной проблемы. (10 мин)
4). Поиск решений учебной проблемы. Подводящий диалог. (7 мин)
5). Физминутка. (1 мин)
6). Закрепление первичных знаний. (13 мин)
7). Подведение итогов урока. (2 мин)
8). Рефлексия. (2 мин)
9). Домашнее задание. (1 мин)
В ходе урока мы рассмотрим постановку проблемной ситуации, формулирование учебной проблемы, поиск решений учебной проблемы и сформулируем подводящий диалог.
|
3. |
Постановка проблемной ситуации. Формулирование учебной проблемы. |
Ребята, постройте в тетрадях три треугольника со сторонами: а) 7, 12, 9 см; б) 7, 14,7 см; в) 5, 16, 7 см. трое учеников выходят к доске работать. В первой задаче треугольник легко построить. Во втором случае получается отрезок, так как три вершины лежат на одной прямой, а треугольник- это фигура, состоящая из трех точек, не лежащих на одной прямой. Можно ли построить треугольник в третьем случае? |
Учитель предлагает ученикам построить треугольники по данным трем сторонам, а трое учеников выходят работать у доски. |
Учащиеся выполняют самостоятельно построения в тетрадях.
Ученики отвечают, что не смогли выполнить третье задание. |
|
4. |
Поиск решений учебной проблемы. Подводящий диалог. |
Вы смогли выполнить задание? В чем затруднение? Какой возникает вопрос? Почему? В каком случае возможно построение треугольника по трем сторонам? В заключении я хочу вам сказать, что эта теорема известна в математике, как «неравенство треугольника». Теперь запишите данную теорему в тетради: «Длина большей стороны меньше суммы длин двух других сторон». |
Учитель ведет побуждающий диалог от проблемной ситуации. Далее переходит к побуждающему диалогу. Если учащиеся не выдвигают никаких гипотез, тогда учитель дает подсказку к решающей гипотезе: «Сравните сумму длин двух меньших сторон и длину большей стороны». |
Почему в третьем случае треугольник не получается. Дело в длинах сторон. Одна сторона больше двух других. Потому что для любого треугольника верно свойство: длина большей стороны меньше суммы длин двух других сторон. Когда длина большей стороны меньше суммы длин двух других сторон. |
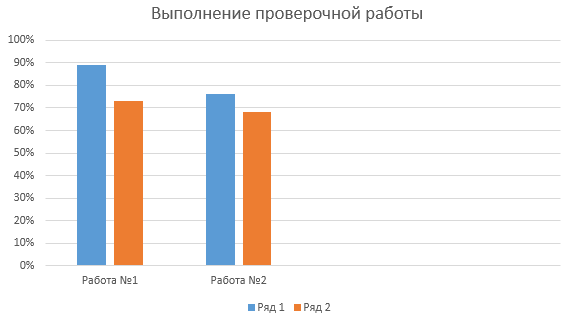
После проведения данного урока с использованием проблемной ситуации была проведена проверочная работа, в результате которой ученики освоили данную тему лучше, чем другие темы уроков, проводимые традиционным методом.
Процент выполнения проверочной работы равен 89%, процент качества равен 73%.
Процент выполнения проверочной работы по урокам, проведенным традиционным методом равен 76%, процент качества равен 68%.
Таким образом, метод проблемного обучения дает ученикам качественные знания, которые они добывают самостоятельно. Тем самым формируются навыки учебно-исследовательской работы школьников, что способствует воспитанию интереса к математике и дальнейшему ее изучению.

 Л.
С. Похольченко
Л.
С. Похольченко