Принципом обеспечения оперативного контроля и самоконтроля в обучении руководствуются все педагоги. Необходимость систематического выявления уровня знаний и умений школьников вытекают из целого ряда обстоятельств. Во-первых, это определяется общественной потребностью иметь информацию о степени эффективности работы школы. Во-вторых, сама структура процесса обучения предполагает наличие обратной связи, без чего невозможно обеспечить регулирование и корректирование этого процесса. В-третьих, контроль выполняет в процессе обучения ряд функций, обеспечивающих повышение результативности учения школьников.
Контроль также является и средством мотивации, осуществляя функцию стимулирования познавательной деятельности учащихся. Однако контроль сможет реализовать данную функцию лишь тогда, когда в каждом конкретном случае будут использоваться «нетрадиционные» средства контроля и их сочетания.
Например, вместо обычной самостоятельной работы можно предложить учащимся решить кросснамбер (кроссворд с цифрами вместо букв). При заполнении его строк и столбцов ученик может сам увидеть и исправить свои ошибки.
Кросснамбер по теме «Умножение и деление натуральных чисел»
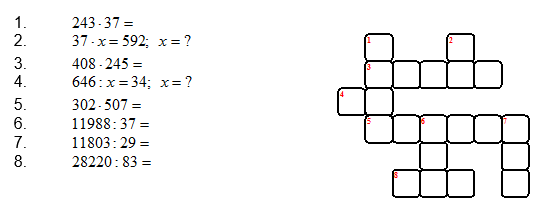
Ещё один вид контроля – это управляемая самостоятельная работа, когда результат одного действия становится условием другого.
Например, управляемая самостоятельная работа по теме «Действия с натуральными числами»
При проверке знаний формул можно предложить учащимся собрать формулы из составных частей, когда на одной карточке написано начало формулы, а на другой – её конец.
Например, набор карточек по теме «Степень с натуральным показателем» (Карточки разрезать)
Подобные карточки можно использовать при проверке знаний формулировок теорем на уроках геометрии. Учащиеся в этом случае должны из разных словосочетаний собрать нужные теоремы. Такую работу можно предложить в конце изучения целой главы.
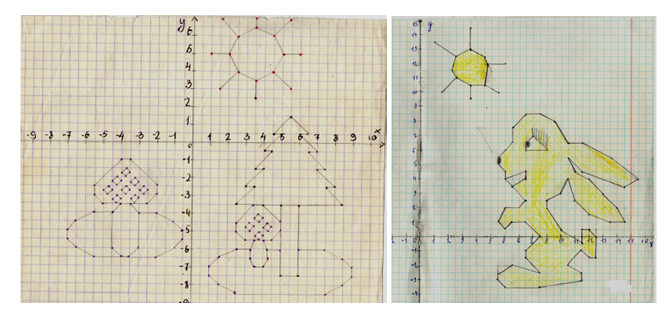
При изучении темы «Координатная плоскость» можно предложить учащимся составить рисунок по заданным точкам или описать данный рисунок координатами точек. В этом случае удобно организовать работу в парах. Можно дать домашнее задание составить и описать рисунок, а на уроке попросить учащихся обменяться работами и выполнить взаимопроверку.
Примеры работ, выполненных учащимися.
Для закрепления работы с формулами удобно применять карточки с пропущенными местами, куда учащиеся вносят свои ответы.
Например, по теме "Формулы сокращенного умножения".
1. (х+1)2= ... ; 5. (х-1)3 =... ; 9. (х+2) (... ) = х2-4;
2. (а-2)2= ... ; 6. (х+2)3 =... ; 10.(3-х) (... ) = 27-х2 ;
3. (2х+3)2= ...; 7. (Зх-2)3 =.. ; 11. (2х+1) (...) = 8х3+1;
4. (Зх-2)2= ... ; 8. (2х+4)3 =… ; 12.(9х2-6х+4)(… ) = 27х3 + 8.
Всегда вызывает у учащихся интерес кодированная самостоятельная работа, где каждый полученный ответ закодирован цифрой или буквой. В результате ученик должен получить закодированное слово или число. Таким способом можно закодировать и новое для детей понятие, а потом перейти к его изучению. Учителю такой вид контроля позволяет мгновенно осуществить проверку.
Например, кодированная самостоятельная работа по теме «Арифметическая прогрессия ».
- Арифметическая прогрессия (аn) задана двумя первыми членами:
3,7; 2,5; …
Найти: d, а3, а4, а5, а6.
- В арифметической прогрессии (хn) х1= 2,5, d= 0,12.
Найти: х26.
Таблица ответов и кодов
|
Таблица ответов и кодов к самостоятельной работе по теме «Арифметическая прогрессия» |
||||||||||||
|
Ответ |
-2,3 |
-1,2 |
-1,1 |
0,1 |
1,3 |
2,8 |
3,1 |
5,5 |
5,9 |
8,7 |
11,5 |
14,9 |
|
Код |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Ответ: 254318
Зачётный урок можно организовать следующим образом. Учащимся предлагается самим выбрать из предлагаемых заданий те, которые он будет решать. В зависимости от набранных баллов ученик получает оценку. Ученик сам определяет уровень своих притязаний.
Например, набор заданий для зачётной работы по теме “Определённый интеграл. Площадь криволинейной трапеции”.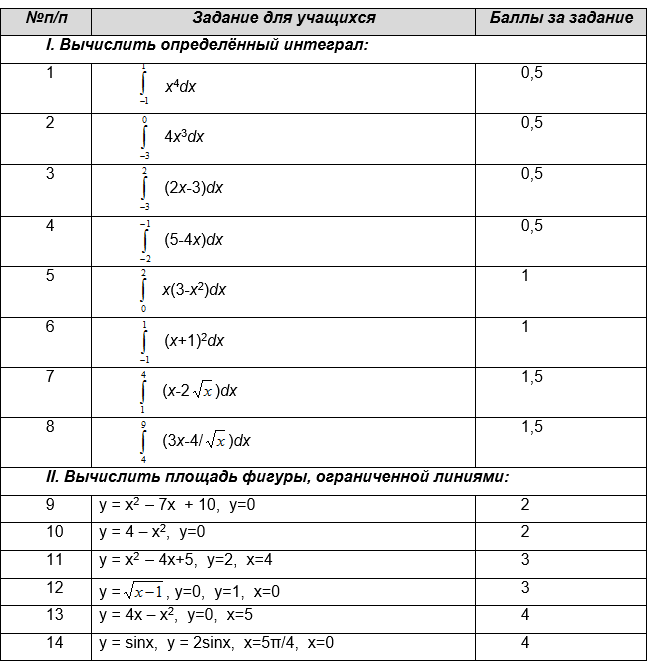
Оценить эту работу можно по следующему принципу: для того, чтобы получить оценку “3”, необходимо набрать 6 – 9,5 баллов, для оценки “4”, необходимо набрать 10 – 14,5 баллов, на оценку “5” – 15 баллов и более.
Почему описанные «нетрадиционные» формы контроля мотивируют познавательную деятельность учащихся? Во-первых, в процессе выполнения таких заданий ученик может сам корректировать свою работу, находить и исправлять свои ошибки. Во-вторых, учащийся узнаёт свою оценку прямо на этом же уроке и, соответственно, имеет возможность её исправить. И, в-третьих, такие формы контроля позволяют ученикам учиться взаимодействовать друг с другом, поскольку можно организовать такую работу в парах и группах.

 Е.
Н. Мазаева
Е.
Н. Мазаева