В последнее время обучающиеся не терпят и не воспринимают математику: несомненно одна из причин связана с тем, что содержание предмета математика не автономное, а системное. Если ученик пропустил занятия, то у него образовывается «яма» незнаний, которую нужно своевременно заполнить. Другая из причин связана с тем, что не учитываются психологические особенности математического мышления обучающихся.
Согласно психологическим исследованиям структуру математического мышления можно рассматривать как пересечение пяти подструктур или кластеров: топологический, проективный, порядковый, метрический, алгебраический (композиционный).
Учащиеся с доминирующим топологическим кластером в первую очередь замечают и легче оперируют такими характеристиками, как непрерывно – разрывно, связно – несвязно, компактно – некомпактно, принадлежит – не принадлежит. Каждое действие делает очень подробно, стараясь не пропустить ни одной операции. Это тонкие аналитики.
Те, у кого доминирует проективный кластер, предпочитают изучать предмет с различных точек зрения, устанавливать соответствие между объектом и его изображением, искать и находить различные применения изучаемого объекта в практике. Они могут отыскать и предлагать совершенно неожиданные подходы и аспекты решения.
Сравнивать, классифицировать и оценивать в общем, качественном виде (больше – меньше, ближе – дальше, выше – ниже, до – после) предпочитают те, у кого доминирует порядковый кластер. Эти юные педанты, которые действуют логично, последовательно, по порядку.
Учащиеся с доминирующим метрическим кластером акцентируют свое внимание на количественных характеристиках. Главный вопрос для них – «сколько?»: какова длина, площадь, расстояние… Им трудно понять, что ответ может не иметь числового значения. Гораздо приятнее для них решать задачу по действиям, результатом каждого из которых является число, нежели искать принцип решения.
Учащиеся с доминирующим алгебраическим кластером стремятся ко всевозможным комбинациям и манипуляциям. Это «торопыги», которые в противоположность «топологам» не хотят подробно записывать, объяснять все шаги решения. Эти великие «комбинаторы» думают, делают быстро, но при этом часто ошибаются
Психологической службой техникума для выявления психологических особенностей студентов проведено тестирование среди студентов групп по профессии «ювелир» (гр. Ю-32) и «электромонтажник электрических сетей и электрооборудования» (гр. ЭМ-24). В группе Ю-32 обучаются в основном девушки (80%), в группе ЭМ-24 – парни.
В исследовании приняли участие 60 человек. Целью диагностирования является анализ математического мышления студентов. По полученным результатам сформирована схема психолого-педагогической характеристики студентов
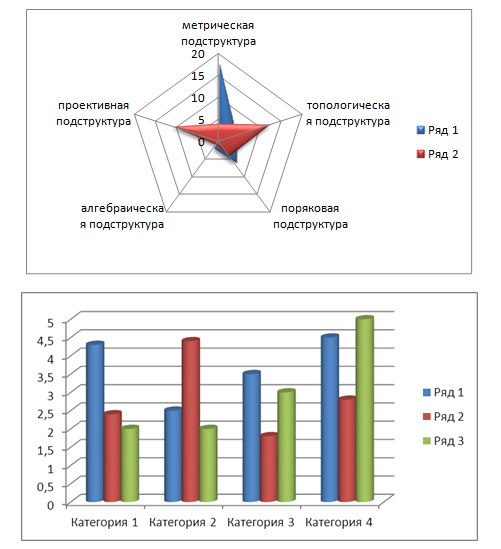
Схема психолого-педагогической характеристики студентов
Психологические исследования показывают, что овладеть иным способом рассуждения человек может лишь после, того как он овладел своим «родным» методом решения проблемы. Отсюда следует вывод о том, что каждую задачу учащийся должен сначала решить своим индивидуальным способом и лишь после этого пытаться понять иные методы рассуждений.
Например, представители этих пяти кластеров одну задачу могут решить пятью способами и прийти к правильному ответу.
Сформировать структуру математического мышления – значит сформировать каждый из указанных кластеров каждому обучающемуся.
Доминантная подструктура математического мышления проявляет себя во всех математических действиях, и в зависимости от нее каждый обучающийся выбирает свой индивидуальный метод решения. Понятно, что далеко не всем учащимся в будущем придется пользоваться логарифмами, составлять уравнения плоскости или сферы, а способность логически рассуждать или доказательно убеждать потребуется каждому. И делать это каждый человек будет не по общей схеме, а в индивидуальной, присущей лично ему манере.
В связи с вышеизложенным возникает проблема психологически грамотного построения урока, который строился бы дифференцированно в зависимости от индивидуальных особенностей математического мышления обучающихся. В соответствии со своей ведущей подструктурой обучающийся по разному воспринимает, оперирует, перерабатывает и воспроизводит математическую информацию. На занятии каждый обучающийся получает возможность решать любую задачу с опорой на свой доминантный кластер. После того как обучающийся осмыслил задачу в рамках своего кластера, он способен понять рассуждения, сделанные другими обучающимися в рамках другого кластера. Описанный подход приводит, во-первых, к непроизвольному развитию слаборазвитых подструктур у обучающихся, а значит, и математического мышления в целом. Во-вторых – исчезают боязнь неуспеха, страх перед задачей, повышается самооценка в данном виде деятельности.

 В.
Р. Крюкова
В.
Р. Крюкова