В настоящее время ФГОС НОО предъявляет такие требования к урокам в начальном звене, что главными задачами учебного процесса становятся не только изучение основных дисциплин, но и приобретение младшими школьниками целостного представления об окружающем мире, развитие у учащихся творческих способностей и трудовых навыков, организация процесса самостоятельного приобретения теоретических и практических знаний и их углубление [1].
ФГОС предъявляет требования во всем предметам начального курса, от реализации которых зависит качество образования каждого учащегося. Считается, что для младших школьников самым сложным для понимания предметом является математика.
Математика - фундаментальный предмет начального школьного обучения, состоящий из разных разделов. Важным разделом курса математики является геометрический материал, который не изучается в какой-то определённый период учебного процесса, а рассматривается в течение всей начальной школы, органично вплетаясь в изучение других тем. Одной из сложных тем, изучаемых третьеклассниками, является «Геометрические величины», которая включает в себя знакомство учащихся со свойствами и особенностями предметов и явлений, новыми величинами и их единицами измерений, а также формирование практических умений и трудовых навыков детей пользоваться измерительными инструментами в повседневной жизни.
Н.Б. Истомина выделила особенности понятия «величина». Величина – это:
- свойство предмета;
- свойство предметов, позволяющее сравнивать объекты в равной мере;
- это свойство, которое определяет, какой из предметов обладает тем или иным свойством в большей степени [2].
Изучение темы «Геометрические величины» происходит по схеме:
1. Сравнение учащимися величины «на глаз».
2. Знакомство с единицами измерения величины, сравнение с ранее изученными.
3. Преобразование величин.
4. Сравнение величин путём измерения.
5. Осуществление операций над величинами и единицами измерений [3].
Любой класс состоит из учащихся с неодинаковым развитием и степенью подготовленности, разной успеваемостью и разным отношением к учению, разными интересами и состоянием здоровья. Чтобы ученик мог реализовать себя, свои индивидуальные особенности, стал субъектом учения, желающим и умеющим учиться, педагогу необходимо создавать определенные условия в процессе обучения.
Шелыгина О.Б. и Каткова А.С. считают, что одним из средств решения данной проблемы является внедрение дифференцированного подхода в учебный процесс. «Дифференцированный подход – это способ организации учебного процесса, при котором для более эффективного обучения выявляются индивидуально-типологические особенности учеников, на основе чего создаются группы учащихся» [4].
Учитывая то, что тема «Геометрические величины» направлена на формирование знаний и умений, необходимых каждому человеку в жизни целесообразно на уроках математики материал для изучения данной темы давать школьникам в соответствии с их уровнем обученности и обучаемости.
Используя дифференцированное обучение на уроках математики, учителю необходимо делить класс на группы, объединенные одним уровнем усвоения учебного материала по теме «Геометрические величины». Также следует младшим школьникам давать возможность самостоятельно выбирать уровень выполнения задания: «А» - низкий уровень, «В» - средний уровень, «С» - высокий уровень, тем самым способствовать формированию адекватной самооценки у учащихся.
Мы предлагаем в данной статье рассмотреть процесс формирования знаний и умений по теме «Геометрические величины» посредством дифференцированного подхода на примере заданий, ориентированных на формирование умений у учащихся преобразовывать, сравнивать и выполнять арифметические действия с единицами измерения длины.
1. Преобразование исходных единиц измерений.
«А». Переведите единицы измерений в заданные. Воспользуйтесь карточкой помощницей.
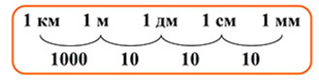
|
6 cм = … мм 11 дм = … cм |
32 м = … см 8 км = … м |
55 км = … дм 48 м = … мм |
«В». На месте пропусков впишите числовые данные и необходимые единицы измерений.
|
54 км = 54 000 … 6 cм = 60 … |
12 cм = … дм … cм 133 мм = … cм … мм |
70 … = 7 … 65 … = 6500 … |
«C». Переведите римские цифры в арабские. Запишите преобразованные единицы измерений арабскими цифрами.
|
V мм = … cм IV км IХ дм = … дм |
ХХI см = … дм … cм III м VI см = … м … cм |
VII м2 = … дм2 I аршин = … cм |
2. Операция cравнения с единицами измерений.
«А». Cравните единицы измерений, используя таблицу «Меры длины.
1 cм = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см = 1000 мм
1 км = 1000 м = 10 000 дм = 100 000 см
|
6 м … 60 дм 54 см … 5400 мм |
21 дм … 210 cм 900 cм … 9 м |
76 км … 7600 м 38 м … 380 000 мм |
«В». Расставьте знаки >,< или =. Раcпределите примеры для cравнения в соответствующие столбики.
7 см … 70 мм, 33 м … 3300 дм, 63 дм … 603 см, 29 км … 29000 м, 85 м …850 000 мм
|
< |
= |
> |
|
|
|
|
«С». Запишите известный фразеологизм. Расшифровать первые два слова тебе помогут примеры для сравнения: ___________________________________________.
|
45 см … 4 дм 50 мм (М) |
87 см … 87 мм (Й) |
2 м 9 см … 290 см (О) |
|
> |
< |
= |
|
|
|
|
|
4 км 28 м …4280 м(O) |
62 дм 55 мм … 620 см 55 мм (Д) |
6 м 43 см 6 м 403 мм (М) |
|
= |
< |
> |
|
|
|
|
3. Арифметические действия с единицами измерений.
«А». Выполните операции сложения и вычитания с единицами измерений. Воспользуйтесь пустой строкой, где запишите только числовые данные, полученные при переводе единиц измерений в заданные.
|
25 дм + 34 м = … дм _________________ 51 см – 32 мм = … мм _________________ |
32 км – 60 м = … м ___________________ 320 см + 11 дм = … см ___________________ |
78 м – 540 см = … см __________________ 4 дм 2см + 8 дм 40см = … см ________________________
|
«В». Вычислите примеры, используя словестные формулировки выражений. Запишите самостоятельно два примера.
1.Восемь дециметров три сантиметра - четыре дециметра девять миллиметров= ….
2. Пять дециметров пять сантиметров + дециметр три сантиметра = …
3. Двадцать метров пять дециметров – двадцать четыре дециметра = …
4. Сорок семь сантиметров + семь метров четыре сантиметра = …
5. Два километра одиннадцать метров – восемь метров = …
6. Восемнадцать дециметров + километр восемь дециметров = …
7. _____________________________________________________________________.
8. _____________________________________________________________________.
«С». Расставьте знаки «+» и «-» так, чтобы равенства были верными. Пронумеруйте примеры в следующей последовательности:
|
1. |
« - » « + » |
|
2. |
« - » « - » |
|
3. |
« + » « + » |
|
4. |
« + » « - » |
|
|
6м 24дм …5м 43 дм … 2м 40дм = 3м 21дм |
|
|
4см 21мм … 32мм … 2см 48 мм = 2см 5 мм |
|
|
54 км 2 м … 28км … 7км 28 мм = 33км 30 м |
|
|
54дм … 5дм 8 см …4дм 29 см = 63дм 37 см |
«А». Выполните действия умножения и деления с единицами измерений.
|
5 дм * 11 = … 45 см : 5 = … |
6 * 34 дм = … 72 : 6 м = … |
65 * 3 км = … (80 : 10мм) * 5 = … |
«В». Зная правила нахождения неизвестного компонента умножения и деления, решите следующие числовые равенства.
|
64 дм : … = 8 дм 5 * … м = 40 м |
900 мм : … = 9 мм 16 см * … = 128 см |
225 км : … = 45 м 17 дм * … = 102 |
«С». Найдите в словах числа и решите равенства. Попробуйте придумать два примера, используя следующие слова с цифрами внутри: стол, дважды, триумф, витрина, вспять, семьдесят.
(Сорока + витрина (см)) * подвал = 86 см
Сороконожка : едва (м) = 20 м
Трибуна * (сорока + семья (мм)) = 141 мм
Восток : (двадцатилетие + опять) км = 4 км
(Пятидесятилетие + родина (дм)) * семицветик = 357 дм
Таким образом, организуя процесс формирования знаний и умений третьеклассников по теме «Геометрические величины» целесообразнее всего применять дифференцированный подход в образовательной деятельности. Такая организация учебного процесса требует от учителя распределения школьников по группам, основанного на совокупности типичных способностей и возможностей учащихся в обучении. Разработанные задания по теме «Геометрические величины» дают шанс третьеклассникам самостоятельно выбирать тот уровень задания, с которым он может справиться. Такая организация учебной деятельности учитывает возможности каждого школьника и способствует повышению их уровня усвоения учебного материала по данной теме.

 О.
Б. Шелыгина
О.
Б. Шелыгина