Преподавание дисциплин экономико-математического профиля является традиционным для дисциплин прикладной математики и обычно состоит из следующих этапов:
Этап 1 Постановка экономической проблемы и ее качественный анализ.
На этапе выполняется: выделение важнейших черт и свойств моделируемого объекта и абстрагирование от второстепенных; изучение структуры объекта и основных зависимостей, связывающих его элементы; формулирование гипотез, допущений, объясняющих поведение и развитие объекта.
Этап 2 Построение математической модели.
Это этап формализации экономической проблемы, формулирование ее в виде конкретных математических зависимостей и отношений (функций, уравнений, неравенств и т.д.). Следовательно, для получения математической модели сначала вводится система буквенных обозначений элементов реального объекта шкалы для их измерений, а затем, на основе изучения существующих взаимосвязей между этими элементами, составляются отражающие их математические соотношения (уравнения, неравенства и др.).
Этап 3 Математический анализ модели.
Целью этого этапа является выяснение общих свойств модели. Здесь применяются чисто математические приемы исследования. Наиболее важный момент – доказательство существования решений в сформулированной модели (теорема существования). Если удастся доказать, что математическая задача не имеет решения, то необходимость в последующей работе по модели отпадает; следует скорректировать либо постановку экономической задачи, либо способы ее математической формализации. При аналитическом исследовании модели выясняются следующие вопросы: единственно ли решение, какие переменные (неизвестные) могут входить в решение, каковы будут соотношения между ними, в каких пределах и в зависимости от каких исходных условий они изменяются, каковы тенденции их изменения и т.д.
Пожалуй, второй и особенно третий этап экономико-математического моделирования вызывают у студентов наибольшие сложности. В практике преподавания естественных наук теоретические исследования обычно дополняются экспериментальными проверками, которые существенно дополняют изучаемую проблему.
Эксперимент как метод познания, при помощи которого в контролируемых и управляемых условиях исследуются явления действительности, очень популярен в научных исследованиях и их приложениях. Главной задачей эксперимента служат проверка гипотез и предсказание теории, имеющей принципиальное значение. Многие исследователи считают эксперимент главным критерием достоверности научной теории.
В социальных и экономических исследованиях натурный эксперимент осуществить очень трудно, а зачастую и невозможно. Во-первых, контролировать поведение людей в социальных системах трудно, особенно если люди знают, что проводится эксперимент. Ведут себя не адекватно в зависимости от того, что они хотят получить от результатов эксперимента. Во вторых социальные системы обладают свойством необратимости, т.е. если по какой-либо причине эксперимент окажется неудачным повторить его при тех же условиях нереально.
Выход в проведении вычислительного эксперимента. Под вычислительным экспериментом (ВЭ) понимается метод проведения экспериментов с математическими моделями, описывающими поведение сложных систем в некоторый период времени. В современных условиях в связи с постоянным совершенствованием вычислительной техники и совершенствованием программного обеспечения ВЭ становится одним из основных методов научного исследования, зачастую предшествующего, а иногда и подменяющего, натурный эксперимент.
Основу, для проведения ВЭ, составляет триада «Математическая модель – (Численные методы) Алгоритм – Программа» [2, с.186]. где под моделью понимается знаковая модель, представленная в виде совокупности математических соотношений , уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому объекту , процессу, или системе; под численным методом здесь понимается такая интерпретация математической модели («дискретная модель»), которая доступна для компьютерной реализации, в виде программы или информационной технологии реализуемой на компьютере [ 1 ].
Программное обеспечение вычислительного эксперимента базируется на использовании систем программирования и пакетов прикладных программ. Первоначально, когда зарождалась концепция вычислительного эксперимента, тексты программ писались на языках программирования, соответственно этап назывался кодированием алгоритма, что требовало высокого искусства программиста. При этом если возникали изменения в математической модели, например, учитывались новые дополнительные условия или появлялись новые переменные программу приходилось переписывать заново или ставить «заплатки в тексте программы», что явно не способствовало качеству программы. В настоящее время, для проведения ВЭ, часто используют пакеты прикладных программ (ППП).
В настоящее время разработаны совершенные прикладные программные пакеты (ППП) используемые в ВЭ, обладающие мощным сервисом, например Mathematica, MathCad и др. В специализированных ППП алгоритм «спрятан» в теле программы и недоступен конечному пользователю. Пользователь должен довольствоваться лишь конечными результатами используя методы и алгоритмы разработчика.
В тоже время многие специалисты в области вычислительного эксперимента не до оценивают широко распространенный ППП как MS Excel. Функциональные возможности MS Excel, конечно, не такие большие как у специализированных систем, но ничто не сравнится с MS Excel по широте распространения и популярности. Для моделирования MS Excel имеет в структуре большое количество встроенных функций, разделенных на классы, которые позволяют конструировать сложные математические выражения. Наличие средства деловой графики, позволяют получать изображения в декартовой системе координат и трехмерные изображения поверхностей. В состав пакета входят приложения (надстройки), как-то ПОИСК РЕШЕНИЯ (для решения задач оптимизации), АНАЛИЗ ДАННЫХ (статистическая обработка) . В составе MS Excel имеются средства расширения функционального содержимого пакета посредством языка программирования VBA
Некоторые авторы, отмечают как недостаток MS Excel использование простых структур данных (одномерных или двумерных массивов), а также невозможности использования циклов [2]. Но это далеко не так MS Excel в своих разработках мы используем многомерные структуры, а также структуры типа record (запись) , а для реализации итерационных алгоритмов с циклами типа «While» и «Do» режим циклических ссылок.
К сожалению MS Excel отсутствуют процедуры, непосредственно реализующие численные методы, которые необходимы для реализации процедур большинства вычислительных экспериментов, например решения дифференциальных и разностных уравнений, вычисления собственных векторов и собственных значений матриц. Эти методы достаточно хорошо изложены в специальной литературе по вычислительной математике [3], [4]. Для реализации численных методов таких методов сконструированы алгоритмы с использованием арифметических операций, логических переходов, встроенных функций, дополненных макросами VBA. При этом процедуру можно непосредственно представить в виде расчетной схемы, непосредственно в ячейках рабочего листа. При необходимости на рабочем листе MS Excel располагаются объекты управления формой (вкладка ленты Разработчик-группа элементы управления).
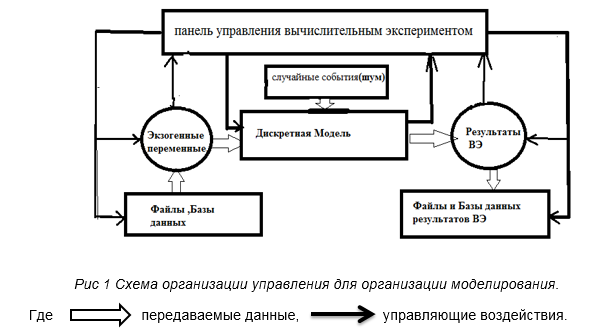
Панель Управления представляет собой Форму, выполненную средствами VBA или рамку, размещенную на рабочем листе MS Excel , на которой размещены объекты управления формой и элементы Activex. Генератор возмущающих воздействий представляет собой датчик случайных чисел, в простейшем случае –это Excel – функция СЛУЧИСЛ, генерирующая случайные числа, равномерно распределённые на отрезке [0,1]. Если априори, известен закон распределения, то в качестве генератора используется метод обратной функции, например, для нормального распределения использована функция НОРМСТОБР (СЛЧИСЛ). Процедура запускается командной кнопкой на форме.
В процессе реализаций процедур ВЭ возникают проблемы связанные:
- с вводом исходных данных из внешних источников (Файлов, баз данных);
- одновременным отображением результатов нескольких реализаций эксперимента, особенно если результаты представляются большими и несвязными наборами данных;
- сохранением и долговременным хранением различных реализаций эксперимента.
Для записи и извлечения данных из других файлов, а также запусков специальных вычислительных процедур использовались элементы управления: «Командные кнопки», «Счетчик», «Полоса прокрутки», «Поле со списком», «Флажки и переключатели», размещаемые на форме. На форме также размещаются командные кнопки: для запуска процедур, управления вводом и выводом результатов в таблицы результатов и в отдельные файлы, обработки статистики результатов, вызова процедур приложения «Анализ данных» и др.. Для каждой командной кнопки написан VBA макрос.
Оценка вычислительной эффективности эксперимента проводилась с точки зрения операций выполняемых пользователем, а не относительно общего числа операций, как принято в вычислительной математике. Особенно эффективны, с точки зрения, реализаций оказались итерационные процедуры, которые позволили рассчитывать общее количество итераций, исследовать сходимость в зависимости от начального приближения и точности вычислений.
Приведенные технологии ВЭ были либо непосредственно использованы при проведении лабораторных занятий дисциплин «Экономико-математические модели», «Численные методы», «Системы принятия решений», «Имитационное моделирование», «Исследования операций», либо разрабатывались в ходе выполнения лабораторных работ по этим дисциплинам.
Некоторые из технологий и процедур, реализующих численные методы. были разработаны студентами специальности «Прикладная информатика в экономике», что особенно полезно при освоении материалов дисциплины «Численные методы». Ряд технологий управляемого вычислительного эксперимента были разработаны студентами указанной специальности в выпускных работах и внедрены на предприятиях, на которых они проходили преддипломную практику.

 Vladimir Vasilev
Vladimir Vasilev