Федеральный государственный образовательный стандарт общего образования предполагает использование образовательных технологий, позволяющих учителю активно применять системно-деятельностный подход, наиболее полно учитывать интересы обучающихся, их склонности, способности, потребности, находить эффективные пути взаимодействия с ними в учебном процессе, анализировать изменения в развитии обучающихся.
В этом аспекте предмет «Математика» открывает большие возможности для формирования системы универсальных учебных действий у обучающихся в рамках учебных занятий.
Для определения структуры конструкта урока математики предлагается использовать научно-методическую систему, основанная на компонентах деятельности, которая разработана в Институте развития образования Свердловской области. На основе ведущих типов деятельности, выделенных в рамках отечественной теории деятельности (Эльконин Д.Б. [1] и др.), выявлены компоненты деятельности – эмоционально-психологический, регулятивный, социальный, аналитический, творческий и самосовершенствования. [2]
Таблица 1.
Формирование компонентов деятельности в процессе онтогенеза в рамках ведущих типов деятельности
|
Тип ведущей деятельности |
Развитие субъектных качеств |
Личностное развитие |
Компоненты деятельности |
|
Непосредственно - эмоциональное общение |
Формирование мотивации |
Эмоционально - психологическое развитие |
Эмоционально - психологический |
|
Предметно-манипулятивная деятельность |
Планирование и организация деятельности |
Ответственность, аккуратность, исполнительность |
Регулятивный |
|
Игровая деятельность |
Работа с информацией, в коллективе |
Социализация в коллективе |
Социальный |
|
Учебная деятельность |
Анализ, планирование |
Нравственность |
Аналитический |
|
Творческая деятельность |
Решение творческих задач |
Креативность |
Творческий |
|
Профессиональная деятельность |
Решение профессиональ ных задач |
Способность к самосовершенство ванию |
Самосовершенст вования |
В соответствии с данными компонентами соотнесены универсальные учебные действия, которые формируются в рамках данных компонентов деятельности.
Таблица 2
Соотношение компонентов деятельности и универсальных учебных действий
|
Компоненты учебной деятельности |
Типы УУД |
Универсальные учебные действия |
|
Эмоционально - психологический |
Личностные |
Мотивация к учению, смыслообразование, нравственно-этическое оценивание |
|
Регулятивный |
Регулятивные (планирование) |
Целеполагание, планирование |
|
Социальный |
Коммуникативные |
Поиск и работа с информацией, планирование и организация совместных действий, сотрудничество |
|
Аналитический |
Познавательные |
Логические действия постановки и решения проблем |
|
Творческий
|
Личностные |
Креативные действия |
|
Самосовершен ствования |
Регулятивные (контроль) |
Контроль, коррекция, оценка |
Каждый этап учебной деятельности способствует формированию определенного вида универсальных учебных действий, что определяет основу структуры конструкта урока [3]:
Таблица 3.
Структура конструкта урока
|
Этап учебной деятельности |
Формируемые компоненты деятельности |
Формируемые УУД |
|
Мотивационный |
Эмоционально – психологический |
Личностные (мотивация) |
|
Принятие цели |
Регулятивный
|
Регулятивные (планирование) |
|
Выбор способов и действий |
Социальный
|
Коммуникативные |
|
Анализ |
Аналитический
|
Познавательные |
|
Творческий этап |
Творческий
|
Личностные (творчество) |
|
Контроль и оценка |
Самосовершенствования
|
Регулятивные (контроль) |
Каждому этапу учебной деятельности соответствует определенный тип универсальных учебных действий. Нецелесообразно указывать все универсальные учебные действия на каждом этапе урока. Необходимо определить «ведущие» универсальные учебные действия на каждом этапе урока.
Эмоционально – психологическому компоненту соответствуют личностные универсальные учебные действия, регулятивному – регулятивные универсальные учебные действия с позиции планирования, целеполагания, социальному – коммуникативные универсальные учебные действия, аналитическому – познавательные универсальные учебные действия, творческому – личностные универсальные учебные действия с позиции творчества, компоненту самосовершенствования – регулятивные универсальные учебные действия с позиции контроля и оценки.
Данная технология разработки конструкта урока позволяет организовать формирующее оценивание личностных качеств обучающихся, развивать их деятельностные способности.
Приведем примеры конструктов уроков по математике:
Конструкт урока по геометрии в 8 классе по теме «Площадь трапеции»
(разработан совместно с учителями математики Алчебаевой Т.В., Крыловой Т.В.)
Пояснительная записка
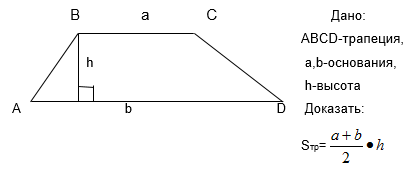
Цель: создать условия для формирования личностных, метапредметных и предметных результатов обучающихся в соответствии с требованиями ФГОС при решении учебной задачи: вывод формулы площади трапеции через ее основания и высоту; применение формулы площади трапеции к решению задач.
Личностные результаты: воспитание готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; формирование осознанного, уважительного и доброжелательного отношения к другому человеку; готовности и способности вести диалог с другими людьми.
Метапредметные результаты:
личностные УУД (мотивация):
умение развивать мотивы и интересы своей познавательной деятельности
регулятивные УУД (планирование):
умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности
коммуникативные УУД:
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов
познавательные УУД:
осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; умение строить логические рассуждения и делать выводы
личностные УУД (творчество):
умение самостоятельно планировать альтернативные пути достижения целей; формулировать, аргументировать и отстаивать своё мнение; регулятивные УУД (контроль и оценка):
умение оценивать правильность выполнения учебной задачи, собственные возможности её решения, владение основами самоконтроля, самооценки; корректировать свои действия в соответствии с изменяющейся ситуацией.
Предметные результаты:
Вывод формулы площади трапеции, нахождение площади трапеции по формуле при решении задач.
Место урока в теме: вводный урок
Характеристика класса:
У обучающихся класса занижена самооценка. В поведении некоторых учащихся преобладают эмоции, они гиперактивны, имеют низкую творческую активность на уроках, не всегда выполняют домашнее задание. Часть учащихся на уроках внимательна, проявляет активность в получении знаний, регулярно выполняет домашнее задание. Такие учащиеся способны анализировать, обобщать, делать выводы, умеют самостоятельно работать на уроке, с большим желанием выполняют индивидуальные задания.
Используемые технологии: проблемное обучение.
Ожидаемые риски достижения цели, способы их избегания: нежелание работать в группах по 4 человека, можно избежать, если выполнять то же задание в парах или индивидуально.
Оборудование, раздаточный материал: компьютер, проектор, экран, набор трапеций из бумаги, таблицы для анализа работы в группах, презентация.
Ход урока:
|
№ |
Этап |
Совместная деятельность |
Ведущие УУД
|
Личностные результаты
|
|||||||||||||||||||||||||||||||||||||||||||||
|
1. |
Мотивационный постановка проблемы |
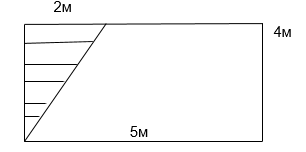
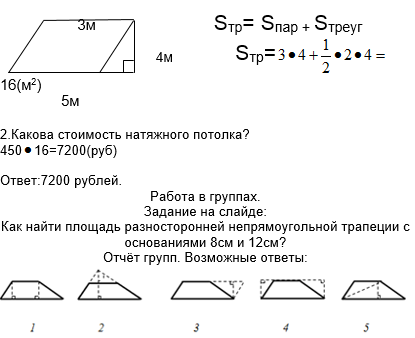
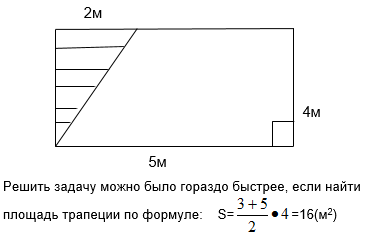
Задача №1: В комнате установлен шкаф, поэтому потолок имеет форму трапеции. Найти стоимость натяжного потолка (без установки), если 1квадратный метр такого полотна стоит 450 рублей. Размеры прямоугольной комнаты смотри на чертеже. |
личностные формирование мотивации |
Развитие познавательного интереса |
|||||||||||||||||||||||||||||||||||||||||||||
|
2. |
Принятие цели планирование деятельности |
Обсуждение проблемы: чего не знаем для решения задачи. Цель урока: научиться находить площадь трапеции.
|
регулятивные целеполагание, действия по образцу |
Ответственность, усвоение этических норм
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3. |
Выбор способов и действий актуализация прошлого опыта,недостаток опытных знаний |
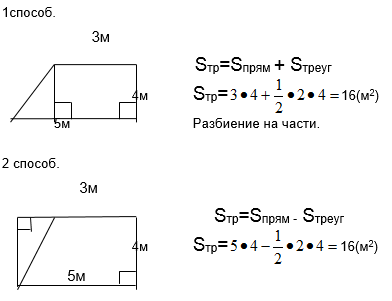
Что необходимо знать для решения этой задачи? Организация индивидуальной работы с последующим коллективным обсуждением. 1.Какова площадь трапеции? |
коммуникативные работа с информацией,работа в коллективе, в группе
|
Любознательность,доброжелательность к другим, усвоение норм морали
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3. |
Выбор способов и действий актуализация прошлого опыта, недостаток опытных знаний |
3 способ. (Каждый ученик из группы самостоятельно решает задачу. Сверяют ответы внутри группы. S=50см2.) |
коммуникативные работа с информацией,работа в коллективе, в группе
|
||||||||||||||||||||||||||||||||||||||||||||||
|
4. |
Анализ
|
Доказать в общем виде теорему о площади трапеции. (Каждый доказывает в группе своим способом) Проверка выполненной работы: По одному представителю группы оформляют доказательство на доске. В это время остальные доказывают теорему с учителем. У каждого ученика на столе таблица. Подписать таблицу. Заполнить пропуски в таблице:
|
познавательные анализ |
Формирование рефлексии |
|||||||||||||||||||||||||||||||||||||||||||||
|
4. |
открытие нового способа действий |
Проверка ответов (внутри группы обменяться таблицами.):
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
5. |
Творческий этап применение способа к новым ситуациям |
Крыша является одним из важных элементов дома. Поэтому к выбору типа крыши, а также к ее обустройству нужно подходить ответственно. Перед вами четырехскатная крыша. Она состоит из четырех скатов. Два ската из четырех соединяются в коньке, а точками соединения остальных скатов являются противоположные концы конька. Причем два ската имеют форму трапеции, а остальные – форму треугольника. Задание: подумайте, какие размеры необходимо знать, чтобы найти количество материалов для постройки крыши. Составьте план расчетов для нахождения площади крыши и количества необходимого материала. Обсуждение в группах. Группа, которая первой ответила на вопросы, докладывает, остальные дополняют. |
личностные творчество
|
Развитие креативных способностей |
|||||||||||||||||||||||||||||||||||||||||||||
|
6. |
Контроль и оценка решение заданий повышеннной сложности
|
Возвращаемся к задаче №1. В комнате установлен шкаф, поэтому потолок имеет форму трапеции. Найти стоимость натяжного потолка (без установки), если 1квадратный метр такого полотна стоит 450 рублей. Размеры прямоугольной комнаты смотри на чертеже.
|
регулятивные контроль, коррекция, оценка
|
Формирование способности к самосовершенствованию |
|||||||||||||||||||||||||||||||||||||||||||||
|
6. |
Контроль и оценка
освоения нового способа действий |
Заполняем листы контроля в группе:
На группу даются оценки: 5,4,3,3. Плюс один дополнительный балл, который вы можете отдать любому участнику группы в качестве поощрения за работу. После заполнения листов контроля распределите оценки внутри группы. Учитель объявляет оценки за урок из листов контроля. |
регулятивные контроль, коррекция, оценка
|
Формирование способности к самосовершенствованию |
|||||||||||||||||||||||||||||||||||||||||||||
Выводы о достижении целей урока:
Цель урока достигнута, выведена формула площади трапеции, рассмотрено применение этой формулы при решении задач, у обучающихся развивались универсальные учебные действия, поскольку учебная деятельность осуществлялась осознанно.
Конструкт урока геометрии в 8 классе по теме «Обратная теорема Пифагора» (разработан совместно с учителем математики Костиной Н.А.)
Пояснительная записка
Цель: создание условий для формирования личностных, метапредметных и предметных результатов обучающихся в соответствии с требованиями ФГОС при решении учебной задачи: вывод обратной теоремы Пифагора, применение её для решения задач.
Личностные результаты: готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, формирование осознанного, уважительного и доброжелательного отношения к другому человеку, готовности и способности вести диалог с другими людьми.
Метапредметные результаты:
личностные УУД (мотивация): умение развивать мотивы и интересы своей познавательной деятельности
регулятивные УУД (планирование): умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности
коммуникативные УУД: умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками
познавательные УУД: осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач
личностные УУД (творчество): умение самостоятельно планировать альтернативные пути достижения целей
регулятивные УУД (контроль и оценка):умение оценивать правильность выполнения учебной задачи, собственных возожностей
Предметные результаты: вывод обратной теоремы Пифагора, применение её для решения задач.
Место урока в теме: вводный урок в теме.
Используемые технологии: проблемное изучение.
Оборудование, раздаточный материал: веревка с узлами, презентация
|
№ |
Этапы урока
|
Совместная деятельность |
Ведущие УУД |
Личностные результаты |
|
1. |
Мотивационный постановка проблемы |
Рассказ учителя о том, как египтяне с помощью веревки, на которой были завязаны узлы по 3, 4 и 5 равных отрезков, выкладывали прямоугольный треугольник. Ученик на парте с помощью веревки выкладывает треугольник со сторонами 3,4,5 Вопрос: «Почему египтяне считали, что против стороны с 5 отрезками в получившемся треугольнике оказывался прямой угол?» |
личностные формирование мотивации |
Развитие познавательного интереса |
|
2. |
Принятие цели планирование
|
Формулируем цель: обосновать теоретически способ получения египтянами прямого угла с помощью веревки
|
регулятивные целеполагание, действия по образцу |
Ответственность, усвоение этических норм
|
|
3. |
Выбор способов и действий актуализация прошлого опыта |
На доске нарисован прямоугольный треугольник с катетами 3 и 4, и треугольник со сторонами 3,4,5. Попытайтесь доказать, что эти треугольники равны по трём сторонам, а значит угол в треугольнике из веревки 90 градусов.
|
коммуникативные работа с информацией, работа в коллективе
|
Любознательность, доброжелательность к другим, усвоение норм морали
|
|
4. |
Анализ освоение нового способа действий |
Доказательство теоремы в общем виде разбираем по учебнику. Решение задач по учебнику.
|
познавательные анализ |
Формирование рефлексии |
|
5. |
Творческий этап применение способа к новым ситуациям |
Мы убедились, что тройка чисел 3,4,5 подчиняется правилу: 32+42=52 , такие тройки называются пифагоровыми. С помощью таблицы квадратов попытайтесь найти другие пифагоровы тройки.
|
личностные творчество
|
Развитие креативных способностей |
|
6. |
Контроль и оценка решение заданий повышеннной сложности
освоения нового способа действий |
Контроль и оценка результата с помощью смайликов
Домашнее задание: найти пифагоровы тройки до 60.. |
регулятивные контроль, коррекция, оценка |
Формирование способности к самосовершенствованию |
Выводы о достижении целей урока:
Цель урока достигнута, выведена формула площади трапеции, рассмотрено применение этой формулы при решении задач, у обучающихся развивались универсальные учебные действия, поскольку учебная деятельность осуществлялась осознанно в соответствии с компонентами деятельности.
Таким образом, представленная методика разработки конструкта урока позволяет педагогу организовать освоение универсальных учебных действий обучающимися на уроках математики для реализации требований федерального государственного образовательного стандарта общего образования, развивать личностные качества, а также организовать формирующее оценивание деятельностных способностей обучающихся.

 Olga Temnyatkina
Olga Temnyatkina