Проблемная обучение – это одна из педагогических технологий, основной задачей которой, является активизация во время занятий интеллектуального потенциала и мыслительной деятельности обучающихся. Проблемные лекции и лекции проблемного характера являются одним из важнейших элементов обучения студентов. Для изложения материала лишь по конкретным проблемам применяются проблемные лекции. Как правило, их используют после того, как студенты освоят основные положения учебного курса. Эти лекции позволяют более углубленно изучить определенные части того или иного учебного предмета. Ведущей формой обучения студентов всех курсов являются лекции проблемного характера, в которых наряду с изложением теоретического, нормативного и практического материала определяется круг проблем, т.е. дискуссионных вопросов, недостаточно разработанных в науке, но имеющих актуальное значение для теории и практики [1].
Таким образом, можно отметить, что проблемная лекция позволяет:
1) дать представление об основных проблемах одного из разделов курса;
2) показать вклад того или иного ученого, научной школы в развитии науки, отдельных ее направлений;
3) углубленно раскрыть узловые и острые проблемы современности.
Кроме того, можно отметить следующие основные цели проблемной лекции:
1) обновить, углубить знания студентов;
2) раскрыть новые научные подходы и разработки важнейших проблем практики;
3) развить культуру научного мышления;
4) сформировать умение самостоятельно ориентироваться в потоке научной информации;
5) активизировать интеллектуальный потенциал студентов, сформировать самостоятельное творческое мышление.
Мы полагаем, что процесс усвоения учебной информации не может быть сведен лишь к ее восприятию, запоминанию и воспроизведению. Только в результате собственной познавательной активности студентов, полученные ими знания, становятся более глубокими. Основой проблемного обучения является формирование активности. В результате чего резко возрастает роль таких видов познавательной деятельности студентов, как поиск ответов на проблемные вопросы, поставленные преподавателем, исследование определенных положений теории и практики, самостоятельное составление и решение нестандартных задач, логический анализ текстов первоисточников, дополнительной литературы [1].
Отметим ряд общих, наиболее важных требований, которые следует учитывать при подготовке и проведении проблемных лекций.
- В проблемной лекции необходимо сосредоточить внимание на наиболее сложных теоретических вопросах, которые имеют большое научное и практическое значение в современных условиях.
- Эффективность проблемной лекции зависит от четкости изложения, логических переходов от одного вопроса к другому, умения подчеркнуть главные положения, сделать необходимые выводы и обобщения.
- Не рекомендуется в проблемных лекциях уходить от дискуссионных вопросов.
- Желательно оставить определенное время для ответов на вопросы, поскольку в ходе лекции невозможно охватить все стороны рассматриваемой проблемы.
- Чтобы обеспечить логическую последовательность изложения материала и его доступность, содержание проблемной лекции всегда должно опираться на использование структурно-логической схемы курса.
- Для усиления внимания студентов, степени восприятия информации, рекомендуется в процессе изложения материала использовать технические и наглядные средства обучения.
Более того, в проблемных лекциях учебная информация не должна излагаться в виде готовых выводов, которые студентам надо запомнить. Такие лекции должны вызывать у студентов познавательный интерес, иначе они теряют свою целенаправленность.
Прежде всего, изложение проблемной лекции целесообразно начать с постановки учебной проблемы, то есть свопроса, ответ на который студентам неизвестен. Но, обладая необходимыми знаниями, они могут приступить к поиску ответа. Проблемная ситуация возникает тогда, когда студенты осознали какое-либо затруднение и потребность в его преодолении. Умение создать проблемную ситуацию в определенный момент лекции – это основная задача преподавателя при проведении проблемной лекции[1].
Рассмотрим пример использования лекции проблемного характера в процессе обучения студентов предметам математического цикла. Студенты экономических специальностей с первого курса изучают математику. Главная задача преподавателя состоит в том, чтобы пробудить интерес к предмету, заложить основы математических знаний, привить умение применять полученные знания при решении конкретных экономических задач. Личный опыт автора статьи показывает, что при преподавании предметов математического цикла студентам экономического направления, представляется целесообразным давать изложение материала в виде проблемной лекции. Это обусловлено тем, что многие студенты проявляют пассивность на занятиях, не подготовлены к работе во время лекции, а проблемная лекция позволит им не только конспектировать новый материал, а самим решать поставленные преподавателем вопросы.
Наибольший интерес у студентов вызывают те разделы математики, которые позволяют наглядно показать, как используются методы математического моделирования в решении конкретных задач планирования и организации производства, финансовых задач, задач регулирования запасов и т.д. По мнению автора, следует с первых занятий на первом курсе ставить перед ними такие задачи в упрощенной форме, которые позволят у учащихся постепенно формировать навыки обращения с математическим аппаратом и способность видеть реальную задачу в математической модели. В результате чего постепенно у студентов складывается отношение к математическому моделированию, как к необходимому инструменту исследования, позволяющему выбрать оптимальный вариант действий из многих допустимых.
Приведем пример решения одной экономической задачи (ее можно предложить студентам направлений «Менеджмент» и «Экономика» при изучении математического анализа (раздел «Теория множеств»)):
Пусть есть два склада С1 и С2 (с однородной продукцией), которые снабжают 3 магазина М1, М2, М3. В начале месяца каждый из магазинов делает заявку на определенное число единиц продукции, т.е. столько, сколько предполагает продать в течение месяца. Это позволяет установить общее количество продукции, которое должно находиться на складах. Магазину М1 требуется 12 ед. продукции, М2 – 10 ед., М3– 9 ед. На складе С1 имеется 13 ед. продукции, на складе С2 – 18 ед. Известна стоимость сijперевозки продукции по каждому из путей от склада Сiдо магазина Mj: с11=8 руб., с12=6 руб., с13=10 руб., с21=9 руб., с22=5 руб., с23=7 руб. Требуется определить, сколько единиц продукции следует отправить с каждого склада в каждый магазин, чтобы общая стоимость перевозок была минимальной[2].
Приведем решение представленной задачи. Пусть х (ед.) продукции требуется перевести со склада С1 в магазин М1, у (ед.) продукции требуется перевести со склада С1 в магазин М2.
Тогда план перевозок задается таблицей.
Таблица 1
|
Склады |
Магазины |
||
|
М1 |
М2 |
М3 |
|
|
С1 |
Х |
у |
13 –х – у |
|
С2 |
12 –х |
10 –у |
х + y - 4 |
Из таблицы находим общую стоимость перевозок S(x,y) = 8x + 6y + 10(13 – x – y) + 9(12 – x) + 5(10 – y) + 7(x + y - 4) = 260 – 4x - 2y.
В таблице все числа должны быть неотрицательными.
олучим следующую систему:
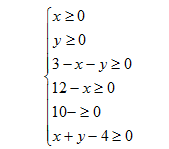
Построим графическое множество решений этой системы, представленное на рисунке 1.
Получили многоугольник решений ABСDEK.
Перед студентами возникает проблема: как из множества точек области ABСDEKнайти ту, в которойфункция S(x,y) принимает минимальное значение.
Из школьного курса математики студенты умеют находить экстремальное значение функции одной переменной. Теперь перед ними возник проблемный вопрос, который необходимо разрешить. Разрешить эту проблему студенты могут уже при изучении следующей темы«Дифференциальное исчисление функций нескольких переменных», а также с помощью методов линейного программирования, теории графов.
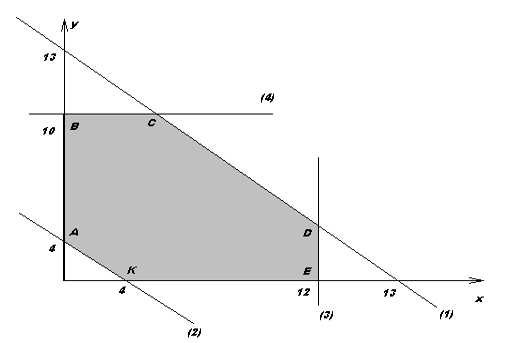
Рисунок 1. Многогранник решений
Эти разделы студенты будут изучать в рамках курсов «Математические методы исследования экономики», «Математическое моделирование экономических систем». При использовании метода линейного программирования данную задачу можно решить либо графическим, либо симплексным методом с использованием соответствующих теорем, или методом потенциалов решения транспортной задачи.
По мнению автора, поставленная перед студентами проблема будет стимулировать их мыслительную деятельность, активизировать интеллектуальный потенциал, и желание решить данную задачу различными способами. Надо отметить, что большой выбор способов решения задачи способствует формированию у студентов умения осуществлять оптимальный выбор в процессе математической деятельности. При этом, студенты рассматривают математический аппарат как инструмент для решения конкретной экономической задачи.
Таким образом, можно сделать вывод, что применение проблемных лекций при преподавании математических дисциплин является важнейшим средством повышения эффективности учебного процесса. Такие лекции позволяют ставить и решать актуальные проблемы курса, увлекательно излагать учебный материал, устанавливать тесный контакт между преподавателем и студентами. Они способствуют вовлечению студентов в процесс познания, раскрывают суть и механизм возникновения и значения тех или иных общественных явлений. В результате этого студенты получают не только прочные знания, но и познавательные навыки, позволяющие им в дальнейшем принимать самостоятельные и обоснованные решения в практической деятельности.

 В.
В. Жолудева
В.
В. Жолудева