Самая важнейшая деятельность человека, показатель его уровня культуры, интеллекта и мышления – его речь.
Н.И. Жинкин считал, что речь является главным видом деятельности человека, а с помощью средств языка реализуется мышление[1].
А по мнению С.И. Ожегова речь служит способом передачи мыслей с помощью языка, а так же речь, как стиль языка, как средство выступления на публике и речь, как звучащий язык[2].
Таким образом, речь - это важнейший вид человеческой деятельности, направленный на передачу собственных мыслей посредством языка. А младший школьный возраст является ступенью усвоения правил языковой системы родного языка. На данной ступени речь у младших школьников становится волевой сферой, т.к. ребенок планирует и обдумывает свой ответ, пытается понять речь, обращенную к нему. В начальной школе ученики овладевают элементарным чтением и письмом. Развивая письменную речь, ученик тем самым обогащает устную речь.
Одной из эффективных форм организации учебного процесса по развитию речи младших школьников является урок математики, так как именно на нем происходит процесс развития всех мыслительных операций при решении различных заданий.
Для эффективности усвоения математической речи учащимися в рамках учебного процесса используются следующие направления работы:
- произношение и употребление математически терминов;
- понимание и умение раскрывать значения математических терминов;
- исключение ошибок и недостатков в речи;
- воспроизведение и использование математической речи в жизненных ситуация.
Одним из действенных способов формирования и углубления математических знаний и умений является организация работы по изучению и решению задач в начальной школе. Шелыгина О.Б. считает, что «задача – это текст с описанием ситуации, в котором содержатся числа, неявно дана связь между ними, а также сформулировано требование найти число, связанное с предложенной ситуацией»[3].
Важным при работе над задачей является её решение. Существует два аспекта в решении задачи: решение как процесс или решение как результат. В первом случае мы находим неизвестное число, обосновывая само действие, а во втором – найдя искомое число, формулируем ответ.
Чтобы научить решать задачи, нужно пройти три ступени:
- Подготовка к введению задач определенного вида
- Обучение решению задач
- Закрепление знаний и умений, приобретённых детьми в процессе решения задач
Решение задачи по математике включает в себя следующие этапы:
- Ознакомление с содержанием
- Поиск путей решения
- Решение задачи
- Проверка
Одним из сложных видов задач для понимания и усвоения детьми являются задачи на умножение и деление.
На уроках математики для учащихся второго класса рекомендуется предлагать задачи на формирование математической речи по следующим направлениям:
I. Работа над звуковой стороной речи.
Задание 1: Бабушка собрала 18 кг грибов. Грибы разложила поровну в 6 банках. Сколько кг грибов в каждой банке?
Задание: прочитайте задачу, правильно проговаривая наименования единиц. Решите ее.
Задание 2: У электрика был провод длиной 18 м, он его разрезал на 3 равные части. Сколько м получилась каждая часть провода?
Задание: прочитайте задачу, правильно проговаривая наименование единиц. Решите задачу.
Данные задачи ориентированы на формирование у детей правильного произношения наименований.
II. Словарная работа с математическими терминами.
Задание 3: Владислава для овечек принесла 12 яблок, а Аркадий 18 яблок. Все яблоки они разложили овечкам в тазы, по 6 яблок в каждом.
Задание: объясните, что обозначают выражения:
12 : 6 18 : 6 12 + 18 (12 + 18) : 6
В первом выражении дайте название компонентов и действия, во втором выражении – какое из чисел можно назвать цифрой, в третьем дайте характеристику каждого числа, четвертое выражение прочитайте разными способами.
Эта задача ориентирована на выявление объектов задачи, связей между данными объектами и на умения читать математические выражения.
Задание 4: В блюде лежало 6 ананасов, а мандаринов на 9 больше. Фрукты разложили в 3 корзины поровну. Сколько фруктов положили в каждую корзину?
Задание: решите задачу, равенства, полученные в каждом действии, прочитайте разными способами.
Данная задача ориентирована на умение читать и записывать математические выражения.
III. Формирование культуры математической речи.
Задание 5: В огороде росло 15 груш по 3 груши в ряд. Сколько рядов с грушами было в огороде? Задание: решите задачу.
Решение задачи:
15 : 3 = 5 (р.) – с грушами было в огороде.
Учитель говорит детям: Альберт прочитал данную запись так: «Произведение пятнадцати и трех равно пяти». София прочитал так: «Частное пятнадцать и три равно пять». А Людмила прочитала так: «Частное чисел пятнадцати и трех равно пяти». Кто прав?
Данная задача предполагает умение чтения математических выражений.
Задание 6: В зоомагазине в 5 аквариумах 20 окуней, поровну в каждом. Сколько аквариумов занимают 16 окуней?
Решение задачи:
1) 20 : 5 = 4 (п.) – в одном аквариуме.
2) 16 – 4 = 12 (ак.) – понадобиться.
Задание: правильно ли я решила задачу? Каким должно быть второе действие?
Эта задача ориентирована на выявление объектов задачи и связей между ними.
IV. Развитие связной математической речи
Задание 7: Составьте задачу по чертежу. Решите ее и составьте задачи, обратные данной.
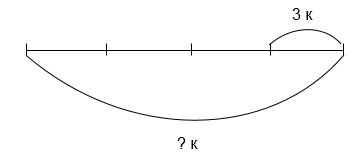
Предложенная задача направлена на воспроизведение объектных ситуаций в словесно-символической форме, запись математических выражений и установление связей между объектами.
Задача 8: На одной парковке стоят 2 джипа. Сколько джипов стоят на 8 таких парковках?
Задание: решите задачу, измените, условие задачи так, чтобы она решалась делением.
Данная задача предполагает умение записывать математические выражения и устанавливать связи между объектами.
Таким образом, данные задания на основе выявленных направлений способствуют развитию математической речи при использовании их на каждом уроке математики при изучении задач на умножение и деление.

 О.
Б. Шелыгина
О.
Б. Шелыгина